NCERT Solutions for Class 7 Maths - Lines and Angles
Exercise 5.1
Q1: Find the complement of each of the following angles:
(i) 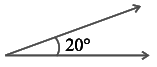 Ans: Two angles are said to be complementary if the sum of their measures is 90º.
Ans: Two angles are said to be complementary if the sum of their measures is 90º.
The given angle is 20º
Let the measure of its complement be xº.
Then,
= x + 20º = 90º
= x = 90º – 20º
= x = 70º
Hence, the complement of the given angle measures 70º.
(ii)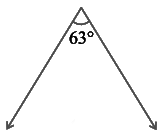 Ans: Two angles are said to be complementary if the sum of their measures is 90º.
Ans: Two angles are said to be complementary if the sum of their measures is 90º.
The given angle is 63º
Let the measure of its complement be xº.
Then,
= x + 63º = 90º
= x = 90º – 63º
= x = 27º
Hence, the complement of the given angle measures 27º.
(iii)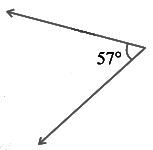
Ans: Two angles are said to be complementary if the sum of their measures is 90º.
The given angle is 57º
Let the measure of its complement be º.
Then,
= x + 57º = 90º
= x = 90º – 57º
= x = 33º
Hence, the complement of the given angle measures 33º.
Q2: Find the supplement of each of the following angles:
(i)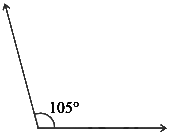
Ans: Two angles are said to be supplementary if the sum of their measures is 180º.
The given angle is 105º
Let the measure of its supplement be xº.
Then,
= x + 105º = 180º
= x = 180º – 105º
= x = 75º
Hence, the supplement of the given angle measures 75º.
(ii)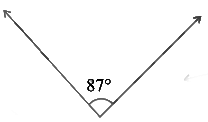
Ans: Two angles are said to be supplementary if the sum of their measures is 180º.
The given angle is 87º
Let the measure of its supplement be xº.
Then, = x + 87º = 180º
= x = 180º – 87º
= x = 93º
Hence, the supplement of the given angle measures 93º.
(iii)
Ans: Two angles are said to be supplementary if the sum of their measures is 180º.
The given angle is 154º
Let the measure of its supplement be xº.
Then,
= x + 154º = 180º
= x = 180º – 154º
= x = 26º
Hence, the supplement of the given angle measures 93º.
Q3: Identify which of the following pairs of angles are complementary and which are supplementary:
(i) 65°, 115°
Ans: We have to find the sum of given angles to identify whether the angles are complementary or supplementary.
Then,
= 65º + 115º
= 180º
If the sum of two angle measures is 180º, then the two angles are said to be supplementary.
∴ These angles are supplementary angles.
(ii) 63°, 27°
Ans: We have to find the sum of given angles to identify whether the angles are complementary or supplementary.
Then,
= 63º + 27º
= 90º
If the sum of two angle measures is 90º, then the two angles are said to be complementary.
∴ These angles are complementary angles.
(iii) 112°, 68°
Ans: We have to find the sum of given angles to identify whether the angles are complementary or supplementary.
Then,
= 112º + 68º
= 180º
If the sum of two angle measures is 180º, then the two angles are said to be supplementary.
∴ These angles are supplementary angles.
(iv) 130°, 50°
Ans: We have to find the sum of given angles to identify whether the angles are complementary or supplementary.
Then,
= 130º + 50º
= 180º
If the sum of two angle measures is 180º, then the two angles are said to be supplementary.
∴ These angles are supplementary angles.
(v) 45°, 45°
Ans: We have to find the sum of given angles to identify whether the angles are complementary or supplementary.
Then, = 45º + 45º = 90º
If the sum of two angle measures is 90º, then the two angles are said to be complementary.
∴ These angles are complementary angles.
(vi) 80°,10°
Ans: We have to find the sum of given angles to identify whether the angles are complementary or supplementary.
Then, = 80º + 10º = 90º
If the sum of two angle measures is 90º, then the two angles are said to be complementary.
∴ These angles are complementary angles.
Q4; Find the angle which is equal to its complement.
Ans: Let one of the two equal complementary angles be x.
∴ x + x = 90°
⇒ 2x = 90°
⇒ x = 90°/2 = 45°
Thus, 45° is equal to its complement.
Q5: Find the angle which is equal to its supplement.
Ans: Let x be two equal angles of its supplement.
Therefore,
x + x = 180° [Supplementary angles]
⇒ 2x = 180°
⇒ x = 180°/2 = 90°
Thus, 90° is equal to its supplement.
Q6: In the given figure, ∠1 and ∠2 are supplementary angles. If ∠1 is decreased, what changes should take place in ∠2 so that both the angles still remain supplementary? 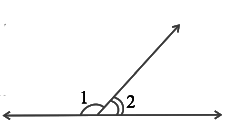
Ans: If ∠1 is decreased then, ∠2 will increase with the same measure, so that both the angles still remain supplementary.
Q7: Can two angles be supplementary if both of them are:
(i) acute
Ans: No. If two angles are acute, means less than 90°, the two angles cannot be supplementary. Because, their sum will be always less than 90°.
(ii) obtuse
Ans: No. If two angles are obtuse, means more than 90°, the two angles cannot be supplementary. Because, their sum will be always more than 180°.
(iii) right?
Ans: Yes. If two angles are right, means both measures 90°, then two angles can form a supplementary pair.
∴ 90° + 90° = 180
Q8: An angle is greater than 45º . Is its complementary angle greater than 45º or equal to 45º or less than 45º ?
Ans: Let the complementary angles be x and y, i.e. p x+ y = 90°
It is given that x > 45°
Adding y both sides, x + y > 45° + y
⇒ 90° > 45° + y
⇒ 90 - 45° > y
⇒ y < 45°
Thus, its complementary angle is less than 45°.
Q9: Fill in the blanks :
(i) If two angles are complementary, then the sum of their measures is __________ .
Ans: 90∘
(ii) If two angles are supplementary, then the sum of their measures is __________.
Ans: 180∘
(iii) If two adjacent angles are supplementary, they form a ______.
Ans: Linear pair
Q10: In the adjoining figure: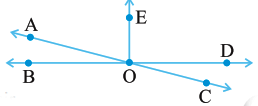
(i) Obtuse vertically opposite angles
Ans: ∠AOD and ∠BOC are obtuse vertically opposite angles in the given figure.
(ii) Adjacent complementary angles
Ans: ∠EOA and ∠AOB are adjacent complementary angles in the given figure.
(iii) Equal supplementary angles
Ans: ∠EOB and ∠EOD are equal supplementary angles in the given figure.
(iv) Unequal supplementary angles
Ans: ∠EOA and ∠EOC are unequal supplementary angles in the given figure.
(v) Adjacent angles that do not form a linear pair
Ans: ∠AOB and ∠AOE, ∠AOE and ∠EOD, ∠EOD and ∠COD are the adjacent angles that do not form a linear pair in the given figure.
Exercise 5.2
Q1: State the property that is used in each of the following statements: 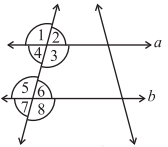
(i) If a║b, then ∠1 = ∠5.
Ans: Given, a║b, then ∠1 = ∠5 [Corresponding angles]
If two parallel lines are cut by a transversal, each pair of corresponding angles are equal in measure.
(ii) If ∠4 = ∠6, then a║b.
Ans: Given, ∠4 = ∠6, then a║b [Alternate interior angles]
When a transversal cuts two lines such that pairs of alternate interior angles are equal, the lines have to be parallel.
(iii) If ∠4 + ∠5 + 180°, then a║b
Ans: Given, ∠4+ ∠5= 180°, then a║b [Co-interior Angles]
When a transversal cuts two lines, such that pairs of interior angles on the same side of transversal are supplementary, the lines have to be parallel.
Q2: In the adjoining figure, identify: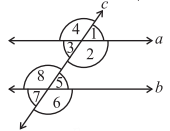
(i) the pairs of corresponding angles.
Ans: The pairs of corresponding angles: ∠1, ∠5; ∠2, ∠6; ∠4, ∠8 and ∠3, ∠7
(ii) the pairs of alternate interior angles.
Ans: The pairs of alternate interior angles are: ∠3, ∠5 and ∠2, ∠8
(iii) the pairs of interior angles on the same side of the transversal.
Ans: The pair of interior angles on the same side of the transversal: ∠3, ∠8 and ∠2, ∠5
(iv) the vertically opposite angles.
Ans: The vertically opposite angles are: ∠1, ∠3; ∠2, ∠4; ∠6, ∠8 and ∠5, ∠7
Q3: In the adjoining figure, p║q. Find the unknown angles.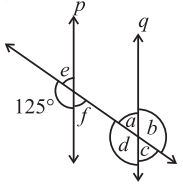
Ans: Given, p║q and cut by a transversal line,
∵ 125°+ e = 180° [Linear pair]
∵ e = 180°-125° = 55° ....(i)
Now e = f = 55° [Vertically opposite angles]
Also a = f = 55° [Alternate interior angles]
a + b = 180° [Linear pair]
⇒ 55° + b = 180° [From equation (i)]
⇒ 6 = 180°- 55°= 125°
Now a = c = 55° and b=d = 125° [Vertically opposite angles]
Thus, a = 55°,b = 125°,c = 55°, d = 125°, e = 55° and f = 55°.
Q4: Find the values of x in each of the following figures if l || m.
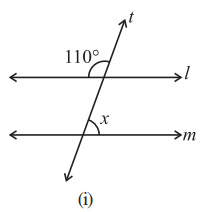 Ans: Let us assume other angle on the line m be ∠y,
Ans: Let us assume other angle on the line m be ∠y,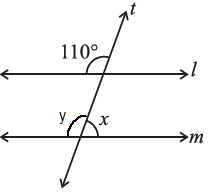
Then, By the property of corresponding angles,∠y = 110°
We know that Linear pair is the sum of adjacent angles is 180°
Then,
= ∠x + ∠y = 180°
= ∠x + 110° = 180°
= ∠x = 180° – 110°
= ∠x = 70°
(ii)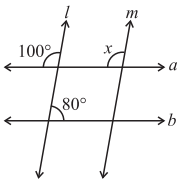 Ans: By the property of corresponding angles,
Ans: By the property of corresponding angles,
∠x = 100°
Q5: In the given figure, the arms of two angles are parallel. If ΔABC = 70o , then find: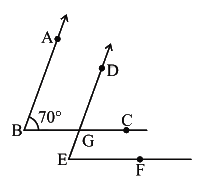 (i) ∠DGC
(i) ∠DGC
Ans: Given, AB ║ DE and BC is a transversal line and ∠ABC = 70°
∴ ∠ABC = ∠DGC [Corresponding angles]
∠ DGC = 70° ........(i)
(ii) ∠DEF
Ans: Given, BC ║ EF and DE is a transversal line and ∠DGC = 70°
∴ ∠DGC = ∠DEF [Corresponding angles]
∠ DEF = 70° [From equation (i)]
Q6: In the given figures below, decide whether l is parallel to m.
(i)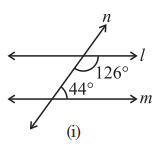
Ans: Let us consider the two lines l and m, n is the transversal line intersecting l and m.
We know that the sum of interior angles on the same side of transversal is 180°.
Then,
= 126° + 44°
= 170°
But, the sum of interior angles on the same side of transversal is not equal to 180°.
So, line l is not parallel to line m.
(ii)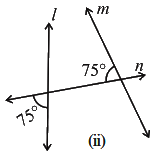
Ans: Let us assume ∠x be the vertically opposite angle formed due to the intersection of the straight line l and transversal n,
Then, ∠x = 75°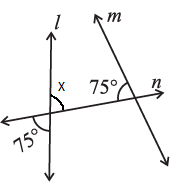
Let us consider the two lines l and m,
n is the transversal line intersecting l and m.
We know that the sum of interior angles on the same side of transversal is 180°.
Then,
= 75° + 75°
= 150°
But, the sum of interior angles on the same side of transversal is not equal to 180o.
So, line l is not parallel to line m.
(iii)
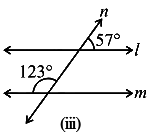
Ans: Let us assume ∠x be the vertically opposite angle formed due to the intersection of the Straight line l and transversal line n,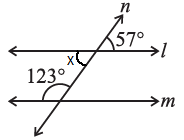
Let us consider the two lines l and m, n is the transversal line intersecting l and m.
We know that the sum of interior angles on the same side of transversal is 180°.
Then,
= 123° + ∠x
= 123° + 57°
= 180°
∴ The sum of interior angles on the same side of transversal is equal to 180°.
So, line l is parallel to line m.
(iv)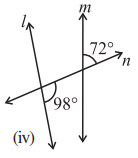 Ans: Let us assume ∠x be the angle formed due to the intersection of the Straight line l and transversal line n,
Ans: Let us assume ∠x be the angle formed due to the intersection of the Straight line l and transversal line n,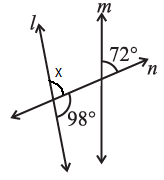
We know that Linear pair is the sum of adjacent angles is equal to 180°.
= ∠x + 98° = 180°
= ∠x = 180° – 98°
= ∠x = 82°
Now, we consider ∠x and 72° are the corresponding angles.
For l and m to be parallel to each other, corresponding angles should be equal.
But, in the given figure corresponding angles measures 82° and 72° respectively.
∴ Line l is not parallel to line m.
|
77 videos|386 docs|39 tests
|
FAQs on NCERT Solutions for Class 7 Maths - Lines and Angles
| 1. What are the basic types of angles in geometry? |  |
| 2. How can we identify parallel lines in geometry? |  |
| 3. What is the relationship between complementary and supplementary angles? |  |
| 4. What are transversal lines and how do they interact with parallel lines? |  |
| 5. How can we prove that two lines are parallel using angles? |  |

















