Patterns and Symmetry Class 4 Notes Maths
| Table of contents |

|
| What is Pattern? |

|
| What is Symmetry? |

|
| Reflection Like a Mirror Image |

|
| Patterns |

|
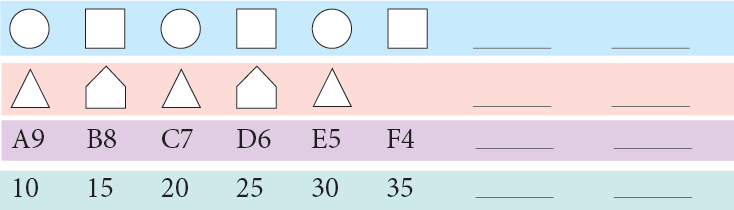
What is Pattern?
A Pattern means repetition in a proper sequence. Patterns can be formed by drawing an image and its reflected image. They can be formed using any Shapes
What is Symmetry?
Symmetry means an object that can be divided exactly into two identical halves of the same size and shapes.
Look at the figures given below and the dotted lines

 If you fold the above figures along the vertical line, you will find that one half exactly covers the other half. Such figures are called the symmetrical figures.
If you fold the above figures along the vertical line, you will find that one half exactly covers the other half. Such figures are called the symmetrical figures.
An object is said to have symmetry if it can be divided into two identical halves. The line that divides the object into its identical halves is called the line of symmetry. For example, in the given image, the line passing through the middle of the flower is its line of symmetry.
What do you think are all objects symmetrical?
No, some objects like the ones given below are not symmetrical. They are called non-symmetrical objects or things.
Reflection Like a Mirror Image
When you look into a mirror, you see your reflection. The mirror image is the reflection of the image.
We can see that a symmetrical shape can be split in half by the line of symmetry. If we put a small mirror on the dotted line, we will see the whole shape. Thus, you can see that a shape has line symmetry when one half of it is the mirror image of the other half.Thus, reflectional symmetry is also known as mirror symmetry.
Look at the reflection of some numbers and letters.
Symmetry in Some Geometrical Shapes
- A square has four lines of symmetry.
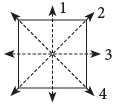
- A rectangle has two lines of symmetry.
- An isosceles triangle has only one line of symmetry.
- An equilateral triangle has three lines of symmetry.
Symmetry in Letters and Numbers
Here are some capital letters and numbers which have lines of symmetry.
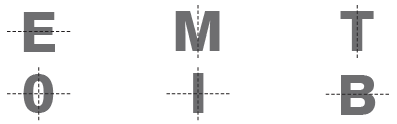 However, there are some letters and numbers which are not symmetrical.
However, there are some letters and numbers which are not symmetrical.
Patterns
Patterns are shapes, designs and a group of numbers that repeat themselves in a predictable manner.
Let us look at some examples.
Patterns in Addition
Patterns of the sum of three consecutive numbers
1 + 2 + 3 = 6, 6 is a multiple of 3 and 3 × 2 = 6.
2 + 3 + 4 = 9, 9 is a multiple of 3 and 3 × 3 = 9.
3 + 4 + 5 = 12, 12 is a multiple of 3 and 3 × 4 = 12.
4 + 5 + 6 = 15, 15 is a multiple of 3 and 3 × 5 = 15.
5 + 6 + 7 = 18, 18 is a multiple of 3 and 3 × 6 = 18.
Rule
The sum of three consecutive numbers is a multiple of 3. Also, the sum is three times the middle term.
Patterns in Multiplication
I. Multiplication of a number ending in 5 by itself.
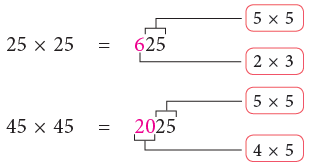
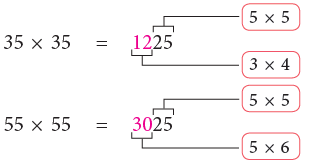
Rule
Every product ends in 25 and the remaining digits are obtained by multiplying the digit at the tens place by its next higher number.
II. Multiplying the same number having all digits as 1.
We have,
1 × 1 = 1
11 × 11 = 121
111 × 111 = 12321
1111 × 1111 = 1234321

Rule
The middle digit in the product is the sum of the digits of one factor.
III. To multiply factors like 19 and 21.
19 × 21 = 399 = 400 – 1 = 20 × 20 – 1
29 × 31 = 899 = 900 – 1 = 30 × 30 – 1
39 × 41 = 1599 = 1600 – 1 = 40 × 40 – 1
Observing the above pattern, we can write
49 × 51 = 50 × 50 – 1 = 2500 – 1 = 2499
59 × 61 = 60 × 60 – 1 = 3600 – 1 = 3599
IV. To multiply a number by 11.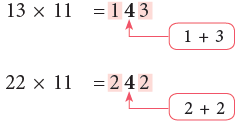
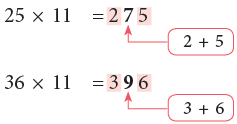
Observing the given pattern,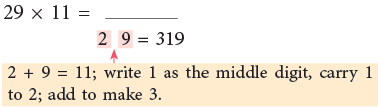
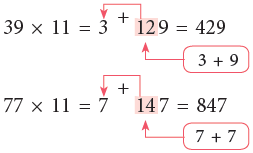
Patterns in Division
Observe the given patterns.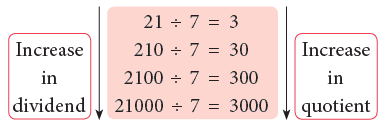
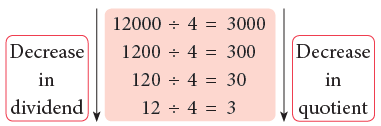
These patterns show that as the dividend increases (divisor remaining the same), the quotient also increases. As the dividend decreases, the quotient also decreases.
Now, keeping the dividend same, let us increase or decrease the divisor and observe the effect on the quotient.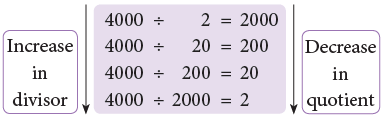
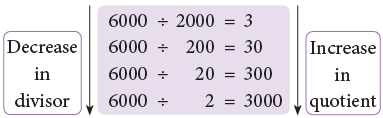
Now, look for the pattern in the following sequence of numbers and find the missing number. 3125, 625, 125, , 5, 1
The missing number is 25, as per the rule for this pattern, the number is divided by 5, each time.
Geometrical Patterns Based on Symmetry
Rangoli patterns are drawn as decorations during the festival of Diwali. The pictures given here show two such patterns.
Now, look at the following patterns.
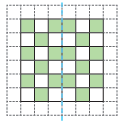
This pattern is symmetrical.
It can be folded in half, so all the lines and colours in each half fit exactly on top of each other.
Quilt patterns based on symmetry.
This pattern is not symmetrical.
When it is folded in half, some of the lines and colours do not match.
|
33 videos|168 docs|30 tests
|
FAQs on Patterns and Symmetry Class 4 Notes Maths
| 1. What is a pattern in mathematics and nature? |  |
| 2. How does symmetry relate to geometry? |  |
| 3. What are the different types of symmetry? |  |
| 4. Can you provide examples of patterns found in nature? |  |
| 5. How can understanding patterns and symmetry benefit students in learning? |  |