RD Sharma Solutions Ex-14.4, (Part - 2), Quadrilaterals, Class 9, Maths | RD Sharma Solutions for Class 9 Mathematics PDF Download
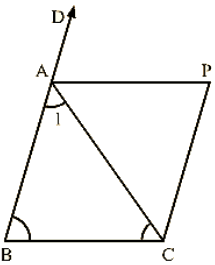
Q.11. In figure 14.98, AB=AC and CP||BA and AP is the bisector of exterior ∠CAD of ∆ABC . Prove that
(i) ∠PAC=∠BCA.
(ii) ABCP is a parallelogram.
Solution:
Given,
AB = AC and CD∥BA and AP is the bisector of exterior ∠CAD of ΔABC
To prove:
(i) ∠PAC = ∠BCA
(ii) ABCP is a parallelogram.
Proof:
(i) We have,
AB=AC
⇒∠ACB = ∠ABC [Opposite angles of equal sides
of triangle are equal]
Now, ∠CAD=∠ABC+∠ACB
⇒∠PAC+∠PAD = 2∠ACB [∴∠PAC = ∠PAD]
⇒2∠PAC = 2∠ACB
⇒∠PAC = ∠ACB
(ii) Now,
∠PAC = ∠BCA
⇒AP∥BC and CP∥BA [Given]
Therefore, ABCP is a parallelogram.
Q.12. ABCD is a kite having AB=AD and BC = CD. Prove that the figure found by joining the mid points of the sides, in order, is a rectangle.
Solution:
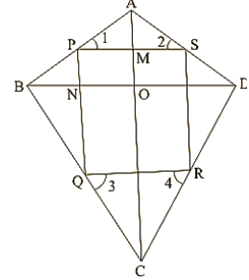
Given,
A kite ABCD having AB=AD and BC=CD. P, Q, R, S are the mid-points of sides AB, BC, CD and DA respectively. PQ, QR, RS and SP are joined.
To prove:
PQRS is a rectangle.
Proof:
In ∆ABC, P and Q are the mid-points of AB and BC respectively.
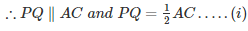
In ∆ADC, R and S are the mid-points of CD and AD respectively.
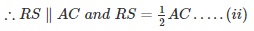
From (i) and (ii) we have
PQ ∥ RS and PQ = RS
Thus, in quadrilateral PQRS, a pair of opposite sides is equal and parallel. So, PQRS is a parallelogram. Now, we shall prove that one angle of parallelogram PQRS is a right angle.
Since AB = AD
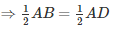
⇒AP = AS….(iii) [∵P and S are mid points of AB and AD]
⇒∠1 =∠2….(iv)
Now, in ΔPBQ and ΔSDR,we have
PB = SD 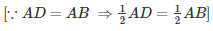
BQ = DR [Since PB = SD]
And PQ = SR [Since, PQRS is a parallelogram]
So, by SSS criterion of congruence, we have
ΔPBQ ≅ ΔSDR
⇒∠3 =∠4[CPCT]
Now, ⇒ ∠3+∠SPQ+∠2 = 1800
And ∠1+∠PSR+∠4 = 1800
∴∠3+∠SPQ+∠2 =∠1+∠PSR+∠4
⇒ ∠SPQ =∠PSR[∠1 = ∠2 and ∠3 =∠4]
Now, transversal PS cuts parallel lines SR and PQ at S and P respectively.
∴∠SPQ+∠PSR = 1800
⇒ 2∠SPQ = 1800
⇒∠SPQ = 900 [∵∠PSR =∠SPQ]
Thus, PQRS is a parallelogram such that ∠SPQ = 900.
Hence, PQRS is a parallelogram.
Q.13. Let ABC be an isosceles triangle in which AB = AC. If D, E, F be the mid points of the, sides BC,CA and AB respectively, show that the segment AD and EF bisect each other at right angles.
Solution:
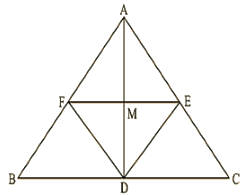
Since D, E and F are mid-points of sides BC, CA and AB respectively.
∴ AB∥DE and AC∥DF
∴ AF∥DE and AE∥DF
ABDE is a parallelogram.
AF = DE and AE = DF
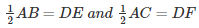
DE = DF [Since, AB = AC]
AE = AF = DE = DF
ABDF is a rhombus.
⇒ AD and FE bisect each other at right angle.
Q.14. ABC is a triangle. D is a point on AB such that AD=1/4AB and E is a point on AC such that AE=1/4AC. Prove that DE=1/4BC.
Solution:
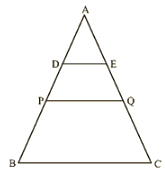
Let P and Q be the mid-points of AB and AC respectively.
Then PQ∥BC
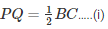
In ΔAPQ, D and E are the mid-points of AP and AQ respectively.
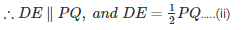
From (i) and (ii): 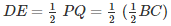
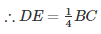
Hence proved.
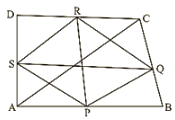
Q.15. In Figure 14.99, ABCD is a parallelogram in which P is the mid-point of DC and Q is a point on AC such that CQ = 1/4AC. If PQ produced meets BC at R, prove that R is a mid-point of BC.
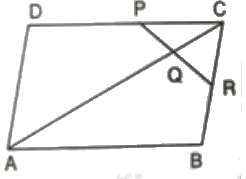
Solution:
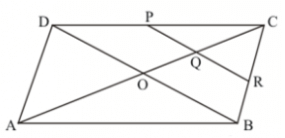
Join B and D.
Suppose AC and BD intersect at O.
Then 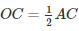
Now,
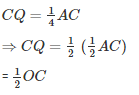
In ΔDCO, P and Q are mid points of DC and OC respectively.
∴ PQ∥DO
Also in ΔCOB, Q is the mid-point of OC and QR∥OB
Therefore, R is the mid-point of BC.
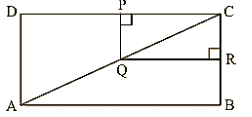
Q.16. In figure 14.100, ABCD and PQRC are rectangles and Q is the mid-point of AC. Prove that
(i) DP = PC 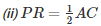
Solution:
(i) In ΔADC, Q is the mid-point of AC such that PQ∥AD
Therefore, P is the mid-point of DC.
⇒ DP = DC [Using mid-point theorem]
(ii) Similarly, R is the mid-point of BC
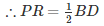
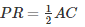 [Diagonal of rectangle are equal, BD = AC]
[Diagonal of rectangle are equal, BD = AC]
Q.17. ABCD is a parallelogram; E and f are the mid-points of AB and CD respectively. GH is any line intersecting AD, EF and BC at G, P and H respectively. Prove that GP = PH.
Solution:
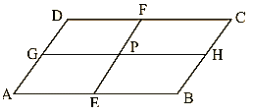
Since E and F are mid-points of AB and CD respectively
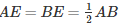
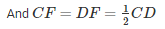
But, AB = CD
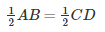
⇒ BE = CF
Also, BE∥CF[∵AB∥CD]
Therefore, BEFC is a parallelogram
BC∥EF and BE = PH …..(i)
Now, BC∥EF
⇒AD∥EF [∵BC∥AD as ABCD is aparallelogram]
Therefore, AEFD is a parallelogram.
⇒ AE = GP
But E is the mid-point of AB.
So, AE = BF
Therefore, GP = PH.
Q.18. BM and CN are perpendiculars to a line passing through the vertex A of triangle ABC. If L is the mid-point of BC, prove that LM = LN.
Solution:
To prove LM = LN
Draw LS as perpendicular to line MN.
Therefore, the lines BM, LS and CN being the same perpendiculars on line MN are parallel to each other.
According to intercept theorem,
If there are three or more parallel lines and the intercepts made by them on a transversal are equal, then the corresponding intercepts on any other transversal are also equal.
In the figure, MB, LS and NC are three parallel lines and the two transversal lines are MN and BC.
We have, BL = LC [As L is the given mid-point of BC]
Using the intercept theorem, we get
MS = SN …. (i)
Now in ΔMLS and ΔLSN
MS = SN using equation (i).
∠LSM =∠LSN=900 [LS⊥MN]
And SL = LS is common.
∴ΔMLS ≅ ΔLSN [SAS CongruencyTheorem]
∴LM = LN [CPCT]
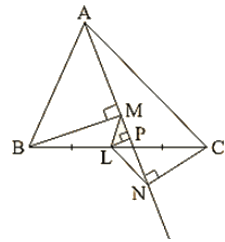
Q.19. Show that, the line segments joining the mid-points of opposite sides of a quadrilateral bisects each other.
Solution:
Let ABCD is a quadrilateral in which P, Q, R and S are mid-points of sides AB, BC, CD and DA respectively.
So, by using mid-point theorem we can say that
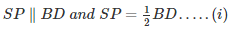
Similarly in ΔBCD
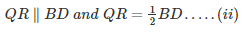
From equations (i) and (ii), we have
SP∥QR and SP = QR
As in quadrilateral SPQR, one pair of opposite sides is equal and parallel to each other.
So, SPQR is a parallelogram since the diagonals of a parallelogram bisect each other.
Hence PR and QS bisect each other.
Q.20. Fill in the blanks to make the following statements correct:
(i) The triangle formed by joining the mid-points of the sides of an isosceles triangle is ____________.
(ii) The triangle formed by joining the mid-points of the sides of a right triangle is ____________.
(iii) The figure formed by joining the mid-points of consecutive sides of a quadrilateral is ____________.
Solution:
(i) Isosceles
(ii) Right triangle
(iii) Parallelogram
FAQs on RD Sharma Solutions Ex-14.4, (Part - 2), Quadrilaterals, Class 9, Maths - RD Sharma Solutions for Class 9 Mathematics
| 1. What are the properties of a quadrilateral? |  |
| 2. What is the difference between a parallelogram and a rectangle? |  |
| 3. How can we prove that a quadrilateral is a parallelogram? |  |
| 4. What is the sum of interior angles of a quadrilateral? |  |
| 5. How can we find the area of a quadrilateral? |  |





















