Chapter 21 - Mensuration - II (Part - 1), Class 8, Maths RD Sharma Solutions | RD Sharma Solutions for Class 8 Mathematics PDF Download
PAGE NO 21.8:
Question 1:
Find the volume of a cuboid whose
(i) length = 12 cm, breadth = 8 cm, height = 6 cm
(ii) length = 1.2 m, breadth = 30 cm, height = 15 cm
(iii) length = 15 cm, breadth = 2.5 dm, height = 8 cm.
ANSWER:
(i)In the given cuboid, we have:
length = 12 cm, breadth = 8 cm and height = 6 cm
∴ Volume of the cuboid = length × breadth × height
= 12 × 8 × 6
= 576 cm 3
(ii)In the given cuboid, we have:
length = 1.2 m
= 1.2 × 100 cm (1 m = 100 cm)
= 120 cm
breadth = 30 cm
height = 15 cm
∴ Volume of the cuboid = length × breadth × height
= 120 × 30 × 15
= 54000 cm³
(iii)In the given cuboid, we have:
length = 1.5 dm
= 1.5 × 10 (1 dm = 10 cm)
= 15 cm
breadth = 2.5 dm = 2.5 × 10 cm = 25 cm
height = 8 cm
∴Volume of cuboid = length × breadth × height
= 15 × 25 × 8
= 3000 cm3
Question 2:
Find the volume of a cube whose side is
(i) 4 cm
(ii) 8 cm
(iii) 1.5 dm
(iv) 1.2 m
(v) 25 mm
ANSWER:
(i)The side of the given cube is 4 cm.
∴ Volume of the cube = (side)3 = (4)3 = 64 cm³
(ii)The side of the given cube is 8 cm.
∴ Volume of the cube = (side)3 = (8)3 = 512 cm³
(iii)The side of the given cube = 1.5 dm = 1.5 × 10 cm = 15 cm
∴ Volume of the cube = (side)3 = (15)3 = 3375 cm³
(iv)The side of the given cube = 1.2 m = 1.2 × 100 cm = 120 cm
∴ Volume of the cube = (side)3 = (120)3 = 1728000 cm³
(v)The side of the given cube = 25 mm = 25/10 cm = 2.5 cm
∴ Volume of the cube = (side)3 = (2.5)3 = 15.625 cm³
Question 3:
Find the height of a cuboid of volume 100 cm³, whose length and breadth are 5 cm and 4 cm respectively.
ANSWER:
Let us suppose that the height of the cuboid is h cm.
Given:Volume of the cuboid = 100 cm³
Length = 5 cm
Breadth = 4 cm
Now, volume of the cuboid = length × breadth × height
⇒ 100 = 5 × 4 × h
⇒ 100 = 20 × h
∴ h = 100/20 = 5 cm
Question 4:
A cuboidal vessel is 10 cm long and 5 cm wide. How high it must be made to hold 300 cm³ of a liquid?
ANSWER:
Let h cm be the height of the cuboidal vessel.
Given:Length = 10 cm
Breadth = 5 cm Volume of the vessel = 300 cm³
Now, volume of a cuboid = length × breadth × height
⇒ 300 = 10 × 5 × h
⇒ 300 = 50 × h
∴ h = 300/50 = 6 cm
Question 5:
A milk container is 8 cm long and 50 cm wide. What should be its height so that it can hold 4 liters of milk?
ANSWER:
Length of the cuboidal milk container = 8 cm
Breadth = 50 cm
Let h cm be the height of the container.It is given that the container can hold 4 L of milk.
i.e., volume = 4 L = 4 × 1000 cm³ = 4000 cm³ (∵ 1 L = 1000 cm³)
Now, volume of the container = length × breadth × height
⇒ 4000 = 8 × 50 × h
⇒ 4000 = 400 × h
⇒ h = 4000/400 = 10 cm
∴ The height of the milk container is 10 cm.
Question 6:
A cuboidal wooden block contains 36 cm³ wood. If it be 4 cm long and 3 cm wide, find its height.
ANSWER:
A cuboidal wooden block contains 36 cm³ of wood.i.e., volume = 36 cm³
Length of the block = 4 cm
Breadth of block = 3 cm
Suppose that the height of the block is h cm
Now, volume of a cuboid = length × breadth × height
⇒ 36 = 4 × 3 × h
⇒ 36 = 12 × h
⇒ h = 36/12 = 3 cm
∴ The height of the wooden block is 3 cm.
Question 7:
What will happen to the volume of a cube, if its edge is
(i) halved
(ii) trebled?
ANSWER:
(i)Suppose that the length of the edge of the cube is x. Then, volume of the cube = (side)3 = x3
When the length of the side is halved, the length of the new edge becomes x/2.
Now, volume of the new cube = (side)3 = (x/2)3 = x3/23 = x3/8 = 1/8 × x3
It means that if the edge of a cube is halved, its new volume will be 1/8 times the initial volume.
(ii)Suppose that the length of the edge of the cube is x. Then, volume of the cube = (side)3 = x3
When the length of the side is trebled, the length of the new edge becomes 3 × x.
Now, volume of the new cube = (side)3 = (3 × x)3 = 33 × x3 = 27 × x3
Thus, if the edge of a cube is trebled, its new volume will be 27 times the initial volume.
Question 8:
What will happen to the volume of a cuboid if its:
(i) Length is doubled, height is same and breadth is halved?
(ii) Length is doubled, height is doubled and breadth is sama?
ANSWER:
(i)Suppose that the length, breadth and height of the cuboid are l, b and h, respectively.
Then, volume = l × b × h
When its length is doubled, its length becomes 2 × l.
When its breadth is halved, its length becomes b/2.
The height h remains the same.
Now, volume of the new cuboid = length × breadth × height
= 2 × l × b/2 × h
= l × b × h
∴ It can be observed that the new volume is the same as the initial volume. So, there is no change in volume.
(ii)Suppose that the length, breadth and height of the cuboid are l, b and h, respectively.Then, volume = l × b × h
When its length is doubled, its length becomes 2 × l.
When its height is double, it becomes 2 × h.
The breadth b remains the same.
Now, volume of the new cuboid = length × breadth × height = 2 × l × b × 2 × h = 4 × l × b × h
∴ It can be observed that the volume of the new cuboid is four times the initial volume.
Question 9:
Three cuboids of dimensions 5 cm × 6 cm × 7 cm, 4 cm × 7 cm × 8 cm and 2 cm × 3 cm × 13 cm are melted and a cube is made. Find the side of cube.
ANSWER:
The dimensions of the three cuboids are 5 cm × 6 cm × 7 cm, 4 cm × 7 cm × 8 cm and 2 cm × 3 cm × 13 cm.
Now, a new cube is formed by melting the given cuboids.
∴ Volume of the cube = sum of the volumes of the cuboids = (5 cm × 6 cm × 7 cm)+(4 cm × 7 cm × 8 cm)+(2 cm × 3 cm × 13 cm)
= (210 cm³)+(224 cm³)+(78 cm³)
= 512 cm³
Since volume of a cube = (side)3, we have:512 = (side)3
⇒ (side) = 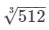 = 8 cm
= 8 cm
∴ The side of the new cube is 8 cm.
Question 10:
Find the weight of solid rectangular iron piece of size 50 cm × 40 cm × 10cm, if 1 cm³ of iron weighs 8 gm.
ANSWER:
The dimension of the rectangular piece of iron is 50 cm × 40 cm × 10 cm.i.e.,
volume = 50 cm × 40 cm × 10 cm
= 20000 cm³
It is given that the weight of 1 cm³ of iron is 8 gm.
∴ The weight of the given piece of iron = 20000 × 8 gm
= 160000 gm
= 160 × 1000 gm
= 160 kg (∵ 1 kg = 1000 gm)
Question 11:
How many wooden cubical blocks of side 25 cm can be cut from a log of wood of size 3 m by 75 cm by 50 cm, assuming that there is no wastage?
ANSWER:
The dimension of the log of wood is 3 m × 75 cm × 50 cm, i.e., 300 cm × 75 cm × 50 cm (∵ 3 m = 100 cm).
∴ Volume = 300 cm × 75 cm × 50 cm = 1125000 cm³
It is given that the side of each cubical block of wood is of 25 cm.
Now, volume of one cubical block = (side)3
= 253
= 15625 cm³
∴ The required number of cubical blocks = 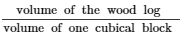
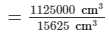
= 72
Question 12:
A cuboidal block of silver is 9 cm long, 4 cm broad and 3.5 cm in height. From it, beads of volume 1.5 cm³ each are to be made. Find the number of beads that can be made from the block.
ANSWER:
Length of the cuboidal block of silver = 9 cm
Breadth = 4 cm Height = 3.5 cm
Now, volume of the cuboidal block = length × breadth × height
= 9 × 4 × 3.5
= 126 cm³
∴ The required number of beads of volume 1.5 cm³ that can be made from the block
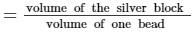
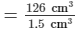
= 84
Question 13:
Find the number of cuboidal boxes measuring 2 cm by 3 cm by 10 cm which can be stored in a carton whose dimensions are 40 cm, 36 cm and 24 cm.
ANSWER:
Dimension of one cuboidal box = 2 cm × 3 cm × 10 cm
Volume = (2 × 3 × 10) cm³ = 60 cm³
It is given that the dimension of a carton is 40 cm × 36 cm × 24 cm, where the boxes can be stored.
∴ Volume of the carton = (40 × 36 × 24) cm³ = 34560 cm³
∴ The required number of cuboidal boxes that can be stored in the carton 
Question 14:
A cuboidal block of solid iron has dimensions 50 cm, 45 cm and 34 cm. How many cuboids of size 5 cm by 3 cm by 2 cm can be obtained from this block? Assume cutting causes no wastage.
ANSWER:
Dimension of the cuboidal iron block = 50 cm × 45 cm × 34 cm
Volume of the iron block = length × breadth × height = (50 × 45 × 34) cm³ = 76500 cm³
It is given that the dimension of one small cuboids is 5cm × 3 cm × 2 cm.
Volume of one small cuboid = length × breadth × height = (5 × 3 × 2) cm³ = 30 cm³
∴ The required number of small cuboids that can be obtained from the iron block 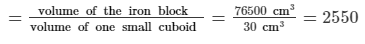
Question 15:
A cube A has side thrice as long as that of cube B. What is the ratio of the volume of cube A to that of cube B?
ANSWER:
Suppose that the length of the side of cube B is l cm.Then, the length of the side of cube A is 3 × l cm.
Now, ratio = 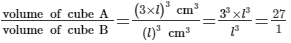
∴ The ratio of the volume of cube A to the volume of cube B is 27:1.
PAGE NO 21.9:
Question 16:
An ice-cream brick measures 20 cm by 10 cm by 7 cm. How many such bricks can be stored in deep fridge whose inner dimensions are 100 cm by 50 cm by 42 cm?
ANSWER:
Dimension of an ice cream brick = 20 cm × 10 cm × 7 cm
Its volume = length × breadth × height = (20 × 10 × 7) cm³ = 1400 cm³
Also, it is given that the inner dimension of the deep fridge is 100 cm × 50 cm × 42 cm.
Its volume = length × breadth × height = (100 × 50 × 42) cm³ = 210000 cm³
∴ The number of ice cream bricks that can be stored in the fridge = 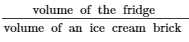
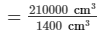 = 150
= 150
Question 17:
Suppose that there are two cubes, having edges 2 cm and 4 cm, respectively. Find the volumes V1 and V2 of the cubes and compare them.
ANSWER:
The edges of the two cubes are 2 cm and 4 cm.
Volume of the cube of side 2 cm, V1 = (side)3 = (2)3 = 8 cm³
Volume of the cube of side 4 cm, V2 = (side)3 = (4)3 = 64 cm³
We observe the following:V2 = 64 cm³ = 8 × 8 cm³ = 8 × V1
∴ V2 = 8V1
Question 18:
A tea-packet measures 10 cm × 6 cm × 4 cm. How many such tea-packets can be placed in a cardboard box of dimensions 50 cm × 30 cm × 0.2 m?
ANSWER:
Dimension of a tea packet is 10 cm × 6 cm × 4 cm.
Volume of a tea packet = length × breadth × height = (10 × 6 × 4) cm³ = 240 cm³
Also, it is given that the dimension of the cardboard box is 50 cm × 30 cm × 0.2 m, i.e., 50 cm × 30 cm × 20 cm (∵ 1 m = 100 cm)
Volume of the cardboard box = length × breadth × height = (50 × 30 × 20) cm³ = 30000 cm³
∴ The number of tea packets that can be placed inside the cardboard box 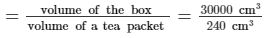 = 125
= 125
Question 19:
The weight of a metal block of size 5 cm by 4 cm by 3 cm is 1 kg. Find the weight of a block of the same metal of size 15 cm by 8 cm by 3 cm.
ANSWER:
The weight of the metal block of dimension 5 cm × 4 cm × 3 cm is 1 kg.
Its volume = length × breadth × height = (5 × 4 × 3) cm³ = 60 cm³
i.e., the weight of 60 cm³ of the metal is 1 kg
Again, the dimension of the other block which is of same metal is 15 cm × 8 cm × 3 cm.
Its volume = length × breadth × height = (15 × 8 × 3) cm³ = 360 cm³
∴ The weight of the required block = 360 cm³
= 6 × 60 cm³ (∵ Weight of 60 cm³ of the metal is 1Kg)
= 6 × 1 kg
= 6 kg
Question 20:
How many soap cakes can be placed in a box of size 56 cm × 0.4 m × 0.25 m, if the size of a soap cake is 7 cm × 5 cm × 2.5 cm?
ANSWER:
Dimension of a soap cake = 7cm × 5 cm × 2.5 cm
Its volume = length × breadth × height = (7 × 5 × 2.5) cm³ = 87.5 cm³
Also, the dimension of the box that contains the soap cakes is 56 cm × 0.4 m × 0.25 m, i.e., 56 cm × 40cm × 25 cm (∵ 1 m = 100 cm).
Volume of the box = length × breadth × height = (56 × 40 × 25) cm³ = 56000 cm³
∴ The number of soap cakes that can be placed inside the box =  = 640
= 640
Question 21:
The volume of a cuboidal box is 48 cm³. If its height and length are 3 cm and 4 cm respectively, find its breadth.
ANSWER:
Suppose that the breadth of the box is b cm.
Volume of the cuboidal box = 48 cm³
Height of the box = 3 cm
Length of the box = 4 cm
Now, volume of box = length × breadth × height
⇒ 48 = 4 × b × 3
⇒ 48 = 12 × b
⇒ b = 48/12 = 4 cm
∴ The breadth of the cuboidal box is 4 cm.
FAQs on Chapter 21 - Mensuration - II (Part - 1), Class 8, Maths RD Sharma Solutions - RD Sharma Solutions for Class 8 Mathematics
| 1. What is the formula for finding the area of a rectangle? |  |
| 2. How do you calculate the volume of a cylinder? |  |
| 3. What is the difference between perimeter and area? |  |
| 4. How do you find the surface area of a rectangular prism? |  |
| 5. How do you determine the circumference of a circle? |  |
















