RD Sharma Solutions Ex-8.2, Lines And Angles, Class 9, Maths | RD Sharma Solutions for Class 9 Mathematics PDF Download
Q 1: In the below Fig. OA and OB are opposite rays:
(i) If x = 25, what is the value of y?
(ii) If y = 35, what is the value of x?
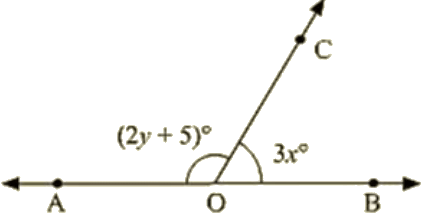
Ans :
(i) Given that,
x = 25
Since ∠AOCand∠BOC form a linear pair
∠AOC+∠BOC = 180∘
Given that ∠AOC = 2y+5 and ∠BOC = 3x
∠AOC+∠BOC = 180∘
(2y + 5) + 3x = 180
(2y +5) + 3 (25) = 180
2y + 5 + 75 = 180
2y + 80 = 180
2y = 180 – 80 = 100
y = 100/2 = 50
y = 50
(ii) Given that,
y = 35
∠AOC+∠BOC = 180∘
(2y+5)+3x = 180
(2(35) + 5) + 3x = 180
(70+5) + 3x = 180
3x = 180 – 75
3x = 105
x = 35
Q 2 : In the below figure, write all pairs of adjacent angles and all the linear pairs.
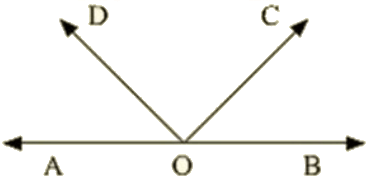
Ans : Adjacent angles are :
(i)∠AOC,∠COB
(ii)∠AOD∠BOD
(iii)∠AOD,∠COD
(iv)∠BOC,∠COD
Linear pairs : ∠AOD,∠BOD,∠AOC,∠BOC
Q 3 : In the given below figure, find x. Further find ∠COD,∠AOD,∠BOC
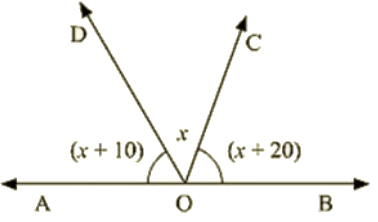
Ans : Since ∠AOD and ∠BOD form a line pair,
∠AOD+∠BOD = 180∘
∠AOD+∠BOC+∠COD = 180∘
Given that,
∠AOD = (x+10)∘,∠COD = x∘,∠BOC = (x+20)∘
- (x + 10) + x + (x + 20) = 180
- 3x + 30 = 180
- 3x = 180 – 30
- 3x = 150/3
- x = 50
Therefore, ∠AOD=(x+10)
= 50 + 10 = 60
∠COD = x = 50∘
∠COD = (x+20)
= 50 + 20 = 70
∠AOD = 60∘∠COD = 50∘ ∠BOC = 70∘
Q 4 : In the Given below figure rays OA, OB, OC, OP and OE have the common end point 0. Show that ∠AOB+∠BOC+∠COD+∠DOE+∠EOA = 360∘
Ans : Given that OA,OB,OD and OE have the common end point O.
A ray opposite to OA is drawn
Since ∠AOB,∠BOF are linear pairs,
∠AOB+∠BOF = 180∘
∠AOB+∠BOC+∠COF = 180∘ —–(1)
Also,
∠AOEand∠EOF are linear pairs
∠AOE+∠EOF = 180∘
∠AOE+∠DOF+∠DOE = 180∘ —–(2)
By adding (1) and (2) equations we get
∠AOB+∠BOC+∠COF+∠AOE+∠DOF+∠DOE = 180∘
∠AOB+∠BOC+∠COD+∠DOE+∠EOA = 180∘
Hence proved.
Q 5 : In the Below figure, ∠AOC and ∠BOC form a linear pair. If a – 2b =30∘, find a and b ?
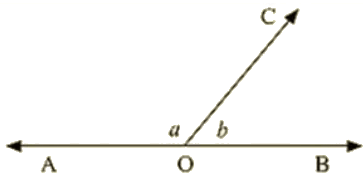
Ans : Given that,
∠AOC and ∠BOC form a linear pair
If a – b = 30
∠AOC = a∘,∠BOC = b∘
Therefore, a +b =180 —–(1)
Given a – 2b = 30 —–(2)
By subtracting (1) and (2)
a+b-a+2b=180-30
- 3b = 150
- b = 150/3
- b = 50
Since a – 2b = 30
a – 2(50) = 30
a = 30 + 100
a = 130
Hence, the values of a and b are 130∘and50∘ respectively.
Q 6 : How many pairs of adjacent angles are formed when two lines intersect at a point ?
Ans : Four pairs of adjacent angles will be formed when two lines intersect at a point.
Considering two lines AB and CD intersecting at O
The 4 pairs are :
(∠AOD,∠DOB),(∠DOB,∠BOC),(∠COA,∠AOD)and(∠BOC,∠COA)
Hence, 4 pairs of adjacent angles are formed when two lines intersect at a point.
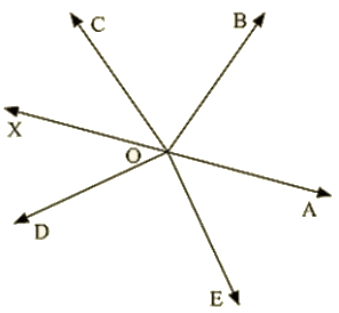
Q 7 : How many pairs of adjacent angles , in all, can you name in the figure below ?
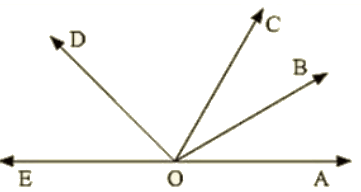
Ans : Pairs of adjacent angles are :
∠EOC,∠DOC
∠EOD,∠DOB
∠DOC,∠COB
∠EOD,∠DOA
∠DOC,∠COA
∠BOC,∠BOA
∠BOA,∠BOD
∠BOA,∠BOE
∠EOC,∠COA
∠EOC,∠COB
Hence, 10 pair of adjacent angles.
Q 8 : In the below figure, find value of x ?
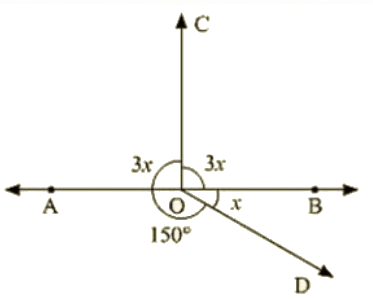
Ans : Since the sum of all the angles round a point is equal to 360∘
- 3x + 3x + 150 + x = 360
- 7x = 360 – 150
- 7x = 210
- x = 210/7
- x = 30
Value of x is 30∘
Q 9 : In the below figure, AOC is a line, find x.
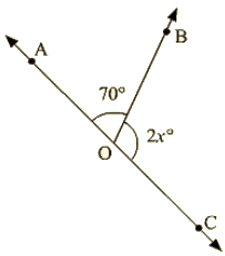
Ans : Since ∠AOBand∠BOC are linear pairs,
∠AOB+∠BOC = 180∘
- 70 + 2x = 180
- 2x = 180 – 70
- 2x = 110
- x = 110/2
- x = 55
Hence, the value of x is 55∘
Q 10 : In the below figure, POS is a line, Find x ?
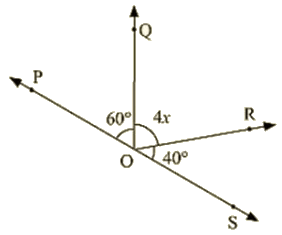
Ans : Since ∠POQand∠QOS are linear pairs
∠POQ+∠QOS = 180∘
- ∠POQ+∠QOR+∠SOR = 180∘
- 60 + 4x +40 = 180
- 4x = 180 -100
- 4x = 80
- x = 20
Hence, Value of x = 20
Q 11: In the below figure, ACB is a line such that ∠DCA=5xand∠DCB=4x. Find the value of x ?
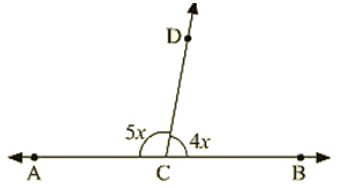
Ans: Here, ∠ACD+∠BCD = 180∘
[Since they are linear pairs]
∠DCA = 5xand∠DCB = 4x
- 5x + 4x = 180
- 9x = 180
- x = 20
Hence, the value of x is 20∘
Q 12 : In the given figure, Given ∠POR = 3x and ∠QOR = 2x+10, Find the value of x for which POQ will be a line ?
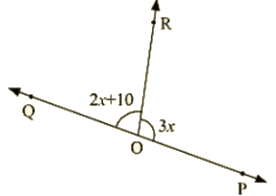
Ans : For the case that POR is a line
∠POR and ∠QORarelinearparts
∠POR+∠QOR = 180∘
Also, given that,
∠POR = 3x and ∠QOR = 2x+10
- 2x + 10 + 3x = 180
- 5x + 10 = 180
- 5x = 180 – 10
- 5x = 170
- x = 34
Hence the value of x is 34∘
Q 13 : In Fig : a is greater than b by one third of a right angle. Find the value of a and b ?
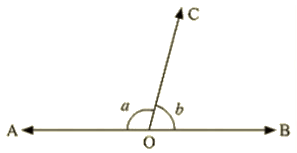
Ans : Since a and b are linear
- a + b = 180
- a = 180 – b —–(1)
From given data, a is greater than b by one third of a right angle
- a = b + 90/3
- a = b + 30
- a – b = 30 —–(2)
Equating (1) and (2)
180 – b = b + 30
- 180 – 30 = 2b
- b = 150 / 2
- b = 75
From (1)
a = 180 – b
- a = 180 – 75
- a = 105
Hence the values of a and b are 105∘ and 75∘ respectively.
Q 14 :What value of y would make AOB a line in the below figure, If ∠AOB=4yand∠BOC = (6y+30)?
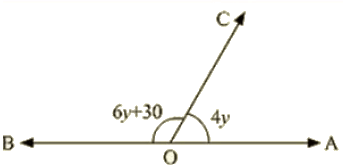
Ans : Since, ∠AOCand∠BOC are linear pairs
∠AOC+∠BOC = 180∘
- 6y + 30 + 4y = 180
- 10y + 30 = 180
- 10y = 180 – 30
- 10y = 150
- y = 150/10
- y = 15
Hence value of y that will make AOB a line is 15∘
Q 15 : If the figure below forms a linear pair,
∠EOB=∠FOC=90 and ∠DOC=∠FOG=∠AOB=30
- Find the measure of ∠FOE,∠COBand∠DOE
- Name all the right angles
- Name three pairs of adjacent complementary angles
- Name three pairs of adjacent supplementary angles
- Name three pairs of adjacent angles
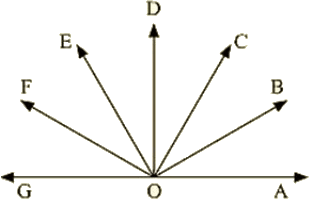
Ans :(i) ∠FOE = x,∠DOE = y and ∠BOC = z
Since ∠AOF,∠FOG is a linear pair
- ∠AOF + 30 = 180
- ∠AOF = 180 – 30
- ∠AOF = 150
- ∠AOB+∠BOC+∠COD+∠DOE+∠EOF = 150
- 30 + z + 30 + y + x = 150
- x + y + z =150 – 30 – 30
- x + y + z =90 —–(1)
∠FOC = 90∘
- ∠FOE+∠EOD+∠DOC = 90∘
- x + y +30 = 90
- x + y = 90 – 30
- x + y =60 —–(2)
Substituting (2) in (1)
x + y + z = 90
- 60 + z = 90
- z = 90 – 60 = 30
Given BOE = 90
- ∠BOC+∠COD+∠DOE = 90∘
- 30 + 30 +DOE = 90
- DOE = 90 – 60 = 30
- DOE = x = 30
We also know that,
x + y = 60
- y = 60 – x
- y = 60 – 30
- y = 30
Thus we have ∠FOE = 30,∠COB = 30 and ∠DOE = 30
(ii) Right angles are ∠DOG,∠COF,∠BOF,∠AOD
(iii) Adjacent complementary angles are (∠AOB,∠BOD);(∠AOC,∠COD);(∠BOC,∠COE);
(iv) Adjacent supplementary angles are (∠AOB,∠BOG);(∠AOC,∠COG);(∠AOD,∠DOG);
(v) Adjacent angles are (∠BOC,∠COD);(∠COD,∠DOE);(∠DOE,∠EOF);
Q16: In below fig. OP, 0Q, OR and OS are four rays. Prove that: ∠POQ+∠QOR+∠SOR+∠POS=360∘
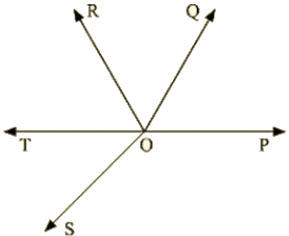
Ans: Given that
OP, OQ, OR and OS are four rays
You need to produce any of the ray OP, OQ, OR and OS backwards to a point in the figure.
Let us produce ray OQ backwards to a point T
So that TOQ is a line
Ray OP stands on the TOQ
Since ∠TOP,∠POQ is a linear pair
∠TOP+∠POQ = 180∘ —–(1)
Similarly,
Ray OS stands on the line TOQ
∠TOS+∠SOQ = 180∘ —–(2)
But ∠SOQ = ∠SOR+∠QOR —–(3)
So, eqn (2) becomes
∠TOS+∠SOR+∠OQR = 180°
Now, adding (1) and (3) you get ∠TOP+∠POQ+∠TOS+∠SOR+∠QOR = 360∘ —–(4)
∠TOP+∠TOS=∠POS
Eqn: (4)becomes
∠POQ+∠QOR+∠SOR+∠POS = 360∘
Q 17 : In below fig, ray OS stand on a line POQ. Ray OR and ray OT are angle bisectors of ∠POSand∠SOQrespectively. If ∠POS = x, find ∠ROT ?
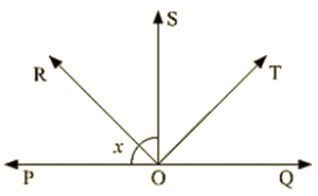
Ans : Given,
Ray OS stand on a line POQ
Ray OR and Ray OT are angle bisectors of ∠POSand∠SOQ respectively
∠POS = x
∠POSand∠SOQ is linear pair
∠POS+∠QOS = 180∘
x + QOS = 180
- QOS = 180 – x
Now, ray or bisector POS
∠ROS=1/2∠POS
- x/2
ROS = x/2 [Since POS = x ]
Similarly ray OT bisector QOS
∠TOS = 1/2∠QOS
= (180 – x)/2 [ QOS = 180 – x ]
= 90 – x/2
Hence, ∠ROT=∠ROS+∠ROT
= x/2 + 90 – x/2
= 90
∠ROT = 180∘
Q 18 : In the below fig, lines PQ and RS intersect each other at point O. If ∠POR:∠ROQ=5:7 . Find all the angles.
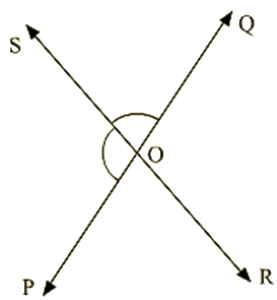
Ans : Given
∠POR and ∠ROP is linear pair
∠POR+∠ROP = 180∘
Given that
∠POR:∠ROQ=5:7
Hence, POR =(5/12)x180=75
Similarly ROQ=(7/7+5) 180 = 105
Now POS = ROQ = 105° [Vertically opposite angles]
Also, SOQ = POR = 75° [Vertically opposite angles]
Q 19 : In the below fig. POQ is a line. Ray OR is perpendicular to line PQ. OS is another ray lying between rays OP and OR. Prove that ∠ROS = 1/2(∠QOS–∠POS).
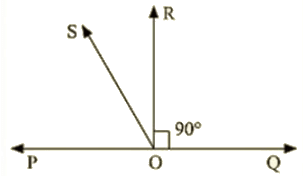
Ans : Given that
OR perpendicular
∴ ∠POR=90∘
∠POS+∠SOR=90 [∵ ∠POR=∠POS+∠SOR]
∠ROS=90°−∠POS —–(1)
∠QOR = 90 (∵ OR ⊥ PQ)
∠QOS–∠ROS = 90∘
∠ROS=∠QOS−90∘
By adding (1) and (2) equations, we get
2∠ROS =∠QOS–∠POS
∠ROS = 1/2(∠QOS–∠POS)
FAQs on RD Sharma Solutions Ex-8.2, Lines And Angles, Class 9, Maths - RD Sharma Solutions for Class 9 Mathematics
| 1. What are lines and angles? |  |
| 2. What are the different types of angles? |  |
| 3. How do you classify lines based on their position? |  |
| 4. How do you find angles in a triangle? |  |
| 5. How can angles help solve real-life problems? |  |


















