Class 9 Maths Chapter 2 Question Answers - Polynomials

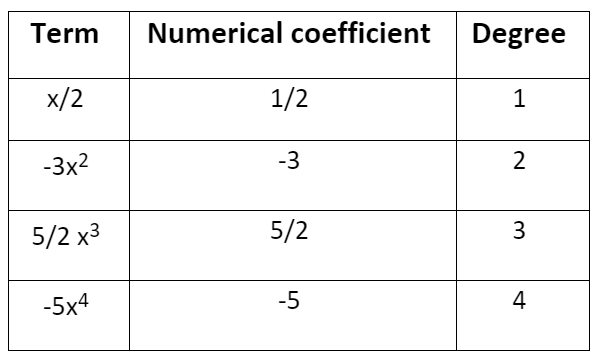
Q1. Write the numerical co-efficient and degree of each term of:

Q2. Find the remainder when x³ – ax² + 4x – a is divided by (x – a).

p(x) = x³ – ax² + 4x – a
(x – a) = 0
⇒ x = a
∴ p(a) = (a)³ – a(a)² + 4(a) – a = a³ – a³ + 4a – a = 4a – a = 3a
∴ The required remainder = 3a.

Q3. Factorise z²  – 4z –12

To factorize this expression, we need to find two numbers α and β such that α + β = -4 and αβ = -12

z² – 6z + 2z – 12

z(z – 6) + 2(z – 6)

(z + 2)(z – 6)

Q4. (a) For what value of k, the polynomial x² + (4 – k)x + 2 is divisible by x – 2?
(b) For what value of ‘m’ is x³ – 2mx² + 16 is divisible by (x + 2)? 

(a) Here p(x) = x² + 4x – kx + 2
If p(x) is exactly divisible by x – 2, then p(2) = 0
i.e. (2)² + 4(2) – k(2) + 2 = 0
⇒ 4 + 8 – 2k + 2 = 0
⇒ 14 – 2k = 0
⇒ 2k = 14
⇒ k= 14/2 = 7
Thus, the required value of k is 7.

(b) Here, p(x) = x³ – 2mx² + 16
∴ p(–2) = (–2)³ –2(–2)²m + 16
⇒ –8 –8m + 16
⇒ –8m + 8
Since, p(x) is divisible by x + 2
∴ p(–2) = 0
or –8m + 8 = 0
⇒ m = 1

Q5. Factorize x² – x – 12.

We have  x² – x – 12
⇒ x² – 4x + 3x – 12
⇒ x(x – 4) + 3(x – 4)
⇒ (x – 4)(x + 3)
Thus, x² – x – 12 = (x – 4)(x + 3)

Q6. If x + (1/2x)  = 5, then find the value of x² +  

We have x + (1/2x)  = 5
Squaring both sides, we get:

⇒
⇒
⇒
Thus, the required value of

Q7. Check whether (x – 1) is a factor of the polynomial x³ – 27x² + 8x + 18.

Here, p(x) = x³ – 27x² + 8x + 18, (x – 1) will be a factor of p(x) only if (x – 1) divides p(x) leaving a remainder 0.
For  x – 1 = 0
⇒ x = 1
∴ p(1) = (1)³ – 27(1)² + 8(1) + 18
⇒ 1 – 27 + 8 + 18
⇒ 27 – 27
⇒ 0
Since, p(1) = 0
∴ (x – 1) is a factor of p(x).
Thus, (x – 1) is a factor of x³ – 27x² + 8x + 18.

Q8. Find the remainder when f(x) =

Here f(x) =  
Divisor = x+(2/3)
since, x+(2/3) = 0 ⇒ x = -2/3
∴ Remainder = f (-2/3)
i.e. Remainder


Thus, the required remainder =  (10/27)

Q9. Find the value of k, if (x – k) is a factor of x⁶ – kx⁵ + x⁴ – kx³ + 3x – k + 4.

Here, p(x) = x⁶ – kx⁵ + x⁴ – kx³ + 3x – k + 4
If (x – k) is a factor of p(x), then p(k) = 0
i.e (k)⁶ – k(k⁵) + k⁴ – k(k³) + 3k – k + 4 = 0
⇒ k⁶ – k⁶ + k⁴ – k⁴ + 3k – k + 4 = 0
⇒ 2k + 4 = 0
⇒ 2k = – 4
⇒ k = (-4/2) = –2
Thus, the required value of k is –2.

Q10. Factorize: 9a² – 9b² + 6a + 1

9a² – 9b² + 6a + 1
⇒ [9a² + 6a + 1] – 9b² 
⇒ [(3a)² + 2(3a)(1) + (1)2] – (3b)² 
⇒ (3a + 1)² – (3b)²
⇒ [(3a + 1) + 3b][(3a + 1) – 3b] {using x² – y² = (x – y)(x + y)}
⇒ (3a + 1 + 3b)(3a + 1 – 3b)

Q11. Find the value of x³ + y³ – 12xy + 64, when x + y = –4.

x³ + y³ – 12xy + 64
⇒ (x)³ + (y)³ + (4)³ – 3(x)(y)(4)
⇒ [x² + y² + 42 – xy – y. 4 – 4 . x](x + y + 4)
⇒ [x² + y² + 16 – xy – 4y – 4x][x + y + 4] ...(1)
Since, x + y = –4 ∴ x + y + 4 = 0                                 ...(2)
From (1) and (2), we have x³ + y³ – 12xy + 64
⇒ [x² + y² + 16 – xy – 4y – 4x][0] = 0
Thus, x³ + y³ – 12xy + 64 = 0.