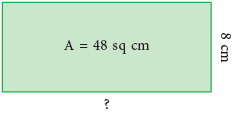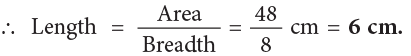Perimeter and Area Class 4 Notes Maths
| Table of contents |

|
| What is Perimeter? |

|
| 1. Perimeter of a Triangle |

|
| 2. Perimeter of a Rectangle |

|
| 3. Perimeter of a Square |

|
| What is Area? |

|
| 1. Area of a Rectangle |

|
| 2. Area of a Square |

|
What is Perimeter?
The perimeter of a shape is the measurement of the total length of the outline of the shape.
Every morning, Sudhir goes for a jog to a park near his house which looks as shown in the given figure. The jogging track is along the boundary of the playground and the lengths of its various parts are as given.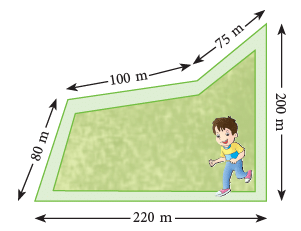 Note: The people who own the park want to put up wire fences around it to keep out unwanted visitors.
Note: The people who own the park want to put up wire fences around it to keep out unwanted visitors.
We call the distance around the park its perimeter.
Thus, the distance around a figure is called its perimeter.
It is found by adding the lengths of the sides of the figure.
Q 1: What is the total distance around the park that requires fencing?
Sol: Total distance around the park that requires fencing
= 100 m + 75 m + 200 m + 220 m + 80 m = 675 m.
Edurev Tips: Perimeter is a Greek word. Peri means around and metrom means measure.
Finding the Perimeter of Figures
We can find the perimeter of a figure, such as given alongside, by counting the number of 1 cm squares along each side of the figure and then adding the lengths of all the sides. ∴ The perimeter of the figure given alongside
∴ The perimeter of the figure given alongside
= 3 cm + 8 cm + 9 cm + 4 cm + 6 cm + 4 cm
= 34 cm.
(a) The perimeter of the figure shown alongside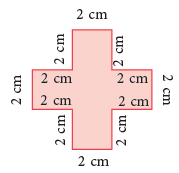
= 2 cm + 2 cm + 2 cm + 2 cm + 2 cm + 2 cm + 2 cm + 2 cm + 2 cm + 2 cm + 2 cm + 2 cm
= (12 × 2) cm = 24 cm
(b) The perimeter of the figure shown alongside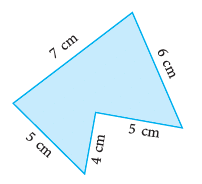 = 7 cm + 6 cm + 5 cm + 4 cm + 5 cm
= 7 cm + 6 cm + 5 cm + 4 cm + 5 cm
= 27 cm
1. Perimeter of a Triangle
We learnt that the perimeter of a simple closed curve made up of the line segments is the sum of the lengths of all the line segments. Let us now find the perimeter of a triangle.
In the case of triangle ABC,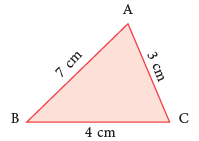 Perimeter of ΔABC = AB + BC + CA
Perimeter of ΔABC = AB + BC + CA
= 7 cm + 4 cm + 3 cm = 14 cm
Thus, the perimeter of a triangle is the sum of the lengths of its sides.
In an equilateral triangle, all the sides are of the same length.
So, the perimeter of an equilateral triangle = side + side + side = 3 × side.
(By side we mean side length.)
2. Perimeter of a Rectangle
Look at the rectangle ABCD, shown below.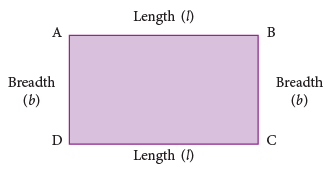 A rectangle has opposite sides of the same measure.
A rectangle has opposite sides of the same measure.
So, perimeter of a rectangle = Sum of the lengths of all line segments.
∴ Perimeter of the rectangle = AB + BC + CD + DA.
= l + b + l + b = 2l + 2b = 2(l + b)
So, Perimeter of a rectangle = 2 (length + breadth).
3. Perimeter of a Square
In a square, all the sides are of equal length.
Look at the square ABCD, shown alongside.
So, perimeter of the square = Sum of the lengths of all line segments.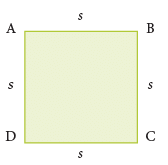 ∴ Perimeter of the square ABCD = AB + BC + CD + DA
∴ Perimeter of the square ABCD = AB + BC + CD + DA
= s + s + s + s = 4s
So, Perimeter of a square = 4 × side.
Example 1: Triangle ABC is an equilateral triangle with all the sides measuring 6 cm each. Find its perimeter.
Perimeter of an equilateral triangle
= 3 × length of one side
= 3 × 6 cm = 18 cm
Thus, the perimeter of the triangle ABC is 18 cm.
Example 2: The measure of a side of a square is 7 cm. Find the perimeter of the square.
The perimeter of the square = 4 × length of one side
= 4 × 7 cm = 28 cm
Thus, the perimeter of the square is 28 cm.
Example 3: The length of the sides AB and CD of the rectangle ABCD are 3 cm each and the length of the sides BC and DA are 6 cm each. Find its perimeter.
Perimeter of rectangle ABCD,
= 3 cm + 6 cm + 3 cm + 6 cm = 18 cm
Using the formula,
Perimeter of the rectangle ABCD = 2(l + b)
= 2 × (6 + 3) cm
= 2 × 9 cm = 18 cm
Thus, the perimeter of the rectangle ABCD is 18 cm.
Example 4: The perimeter of a rectangle is 52 cm. The length of the rectangle is 14 cm. Find its breadth
Perimeter = 52 cm, Length = 14 cm
We know that, Perimeter of a rectangle = 2(l + b)
52 cm = 2(14 cm + b)
52 ÷ 2 cm = 14 cm + b
26 cm = 14 cm + b
26 cm – 14 cm = b
b = 12 cm
Thus, breadth of the rectangle is 12 cm.
Example 5: What is the length of the side of a square whose perimeter is 160 cm?
Given, perimeter = 160 cm.
We know that,
Perimeter of a square = 4 × side = 160 cm
= side = 160 ÷ 4
= side = 40 cm
Thus, measure of one side of the square is 40 cm.
What is Area?
Concept of Area
(i) Take a plate and cover it with the cookies. How many cookies do you need to cover the plate? Now, take another plate of a different size. Which plate needs more cookies? Which plate has a larger surface?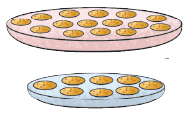 (ii) Rahul wrapped 2 gifts. He found that bigger gift required more wrapping paper, whereas the smaller gift required less wrapping paper. So, by area we mean, the flat surface which you cover or paint.
(ii) Rahul wrapped 2 gifts. He found that bigger gift required more wrapping paper, whereas the smaller gift required less wrapping paper. So, by area we mean, the flat surface which you cover or paint. Thus, area is the measure of the region inside a plane figure.
Thus, area is the measure of the region inside a plane figure.
Finding Area using Square Tiles
Ms. Sharma wanted to know the area of her porch floor. She started, by putting square floor tiles on the floor.
How many more tiles will it take to cover the floor?
Ans: 6
How many tiles will be used altogether?
Ans: 48
An object such as a square paper sheet or a square floor tile can be used to find the area. A square and its interior is called a square unit for finding area.
Thus, area of a region can be found by finding the number of square units needed to cover the interior of a figure.
Example 6: Find the area of each of the following regions by counting squares.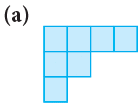
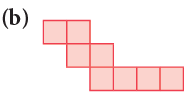
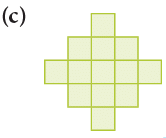
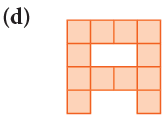
Mark the squares in the figures:
(a) Since there are 7 squares in the figure,∴ Area of the given figure = 7 square units.
(b) Since there are 8 squares in the figure,∴ Area of the given figure = 8 square units.
(c) Since there are 13 squares in the figure,∴ Area of the given figure = 13 square units.
(d) Since there are 12 squares in the given figure,∴ Area of the given figure = 12 square units.
1. Area of a Rectangle
Look at the following rectangle whose length is 7 cm and breadth is 3 cm.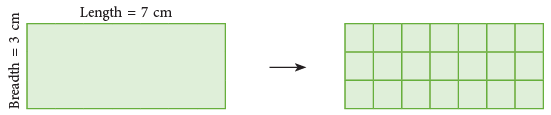 To find its area, we can divide it into 3 rows of 7 squares each or 7 columns of 3 squares each.
To find its area, we can divide it into 3 rows of 7 squares each or 7 columns of 3 squares each.
By counting the number of squares, we can find the area of the rectangle. Since the rectangle contains 21 squares, so its area = 21 square centimetre.
Note that, if we multiply the length (l) = 7 cm and breadth (b) = 3 cm, then we get the product as 21 square centimetre.
Therefore, Area of a rectangle = length × breadth = l × b.
2. Area of a Square
If we divide a square of side 5 cm into small squares by dividing it into 5 rows and 5 columns, we get 25 small squares each of length 1 centimetre.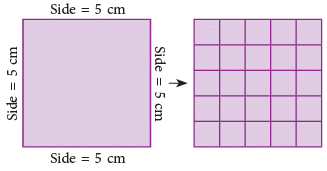 ∴ Area of the square = 25 sq cm (by counting).
∴ Area of the square = 25 sq cm (by counting).
Also, on multiplying 5 cm by 5 cm, we get, 25 sq cm.
Therefore, Area of a square = side × side.
Example 7: Find the area of a rectangle with length 12 cm and breadth 4 cm.
Area of rectangle = l × b
= 12 cm × 4 cm = 48 sq cm.
Example 8: Find the length of a rectangle whose area is 48 sq cm and breadth is 8 cm.
Area = Length × Breadth
Example 9: Find the area of a square field of side length 70 m?
Area of square = Side × Side
= 70 m × 70 m = 4900 sq m.
|
33 videos|168 docs|30 tests
|
FAQs on Perimeter and Area Class 4 Notes Maths
| 1. What is the formula for calculating the perimeter of a triangle? |  |
| 2. How do you find the perimeter of a rectangle? |  |
| 3. What is the formula for the perimeter of a square? |  |
| 4. How is the area of a rectangle calculated? |  |
| 5. What is the formula for calculating the area of a square? |  |