CBSE Sample Paper Solutions 1 Term 1 - Class 7 Maths
| Table of contents |

|
| Mathematics |

|
| Time: 2 ½ Hours |

|
| Maximum Marks: 80 |

|
| Section A |

|
| Section B |

|
| Section C |

|
| Section D |

|
Mathematics
Time: 2 ½ Hours
Maximum Marks: 80
General Instructions:
- All questions are compulsory.
- Section A comprises of 12 questions carrying 1 mark each.
- Section B comprises of 12 questions carrying 2 marks each.
- Section C comprises of 8 questions carrying 3 marks each.
- Section D comprises of 5 questions carrying 4 marks each.
Section A
Q.1. If a, b and c are integers then, according to distributive law
(a) a x (b + c) = a x b + a x c
(b) a x (b + c) = a + b x a + c
(c) a x (b + c) = a x b x a x c
(d) a x (b + c) = a x c - a x b
Ans. (a)
Solution. According to the distributive property of integers, we have
► a x (b + c) = a x b + a x c
Q.2. A number is chosen at random from 1 to 5. What is the probability that the number chosen is odd?
(a) 2 / 5
(b) 3 / 5
(c) 1 / 4
(d) 1 / 6
Ans. (b)
Solution. A number is chosen from numbers 1 to 5.
Odd numbers are 1, 3, 5.
Required probability
= number of ways to choose an odd number / total number of numbers
= 3 / 5
Q.3. The solution of the equation 3x + 4 = 25 is
(a) 7
(b) 8
(c) 9
(d) 6
Ans. (a)
Solution. 3x + 4 = 25
Transposing 4 to R.H.S, we get,
► 3x = 25 - 4
► 3x = 21
Dividing both sides by 3, we get,
► x = 7
Q.4. In the figure given below, the measure of y is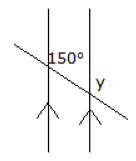 (a) 30º
(a) 30º
(b) 120º
(c) 130º
(d) 150º
Ans. (d)
Solution. Since the angle measuring 150º and y are corresponding angles. Therefore, y = 150º. (As the lines are parallel, corresponding angles are equal).
Q.5. The measure of angle x, in the given figure, is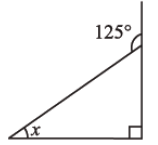 (a) 45º
(a) 45º
(b) 30º
(c) 60º
(d) 35º
Ans. (d)
Solution. We know that the measure of an exterior angle of a triangle is equal to the sum of its two opposite interior angles.
So, x + 90º = 125º
Therefore, x = 35º
Q.6. The integer -2 - (-5) can also be written as
(a) -2 + (-5)
(b) -2 + 5
(c) 2 – 5
(d) 2 + 5
Ans. (b)
Solution. Negative of a negative integer is a positive integer.
So, - (-5) = +5
So, -2 - (-5) = -2 + 5
Q.7. In the following figure, the relation between the angles 1, 2 and 3 is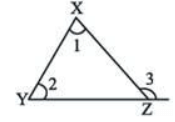 (a) ∠3 = ∠1 - ∠2
(a) ∠3 = ∠1 - ∠2
(b) ∠3 + ∠1 = ∠2
(c) ∠3 = ∠1 + ∠2
(d) ∠3 + ∠2 = ∠1
Ans. (c)
Solution. ∠3 = ∠1 + ∠2
Since the measure of an exterior angle of a triangle is equal to the sum of measures of its two opposite interior angles.
Q.8. Mean of 11, 10, 12, 12, 9, 10, 14, 12, 9 is ______ .
(a) 20
(b) 10
(c) 11
(d) 14
Ans. (c)
Solution. The given observations are 11, 10, 12, 12, 9, 10, 14, 12, 9.
Mean = (11+10+12+9+10+14+12+9)/9 = 99/9 = 11
Q.9. Five added to a one third of a number gives twice the number, then the number is
(a) 3
(b) 4
(c) 5
(d) 6
Ans. (a)
Solution. Let the number = x
One-third of the number
=
Five added to one third of the number
=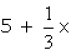
From the given condition, we have:
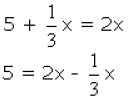
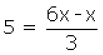
► 5 = 5x / 3
► x = 3
Q.10. In the following figure, the measure of angle x is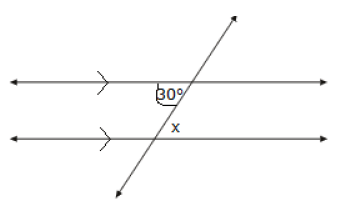 (a) 60º
(a) 60º
(b) 150º
(c) 30º
(d) 45º
Ans. (c)
Solution. Angle x is the alternate angle to angle 30º.
And, since alternate interior angles are equal, x = 30º.
Q.11. The value of x in the following triangle is (a) 6 cm
(a) 6 cm
(b) 8 cm
(c) 5 cm
(d) 2 cm
Ans. (c)
Solution. Since, given triangle is a right angled triangle, we have
x2 = 32 + 42 = 9 + 16 = 25 = 52
Therefore, x = 5 cm
Q.12. Name the pair of congruent triangles in the given figure.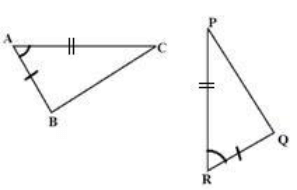
(a) ΔABC ≌ ΔPQR
(b) ΔABC ≌ ΔRQP
(c) ΔBAC ≌ ΔPQR
(d) None of these
Ans. (b)
Solution. Given, AB = RQ, AC = RP, ∠BAC = ∠QRP
Hence, ΔABC ≌ ΔRQP (Using SAS)
Section B
Q.13. What is the measure of complement of each of the following angle?
(a) 45º
(b) 54º
(c) 65º
Ans. To find the complement of each of the given angle, we have to subtract them from 90º, since the sum of two complementary angles is 90º.
(a) Complementary angle of 45º = 90º - 45º = 45º
(b) Complementary angle of 54º = 90º - 54º = 36º
(c) Complementary angle of 65º = 90º - 65º = 25º
Q.14. Write the following equations in statement form:
(a) 6n + 4 = 10
(b) y / 7 - 3 = 9
Ans. (a) 6n + 4 = 10
Statement:
For 6n, Six times of a number n.
For 6n + 4, Six times of a number n added to 4.
Thus, for 6n + 4 = 10, the final statement is:
"Six times of a number n added to 4 gives 10".
(b) y / 7 - 3 = 9
Statement:
For y / 7, one-seventh of a number y
For y / 7 - 3, 3 subtracted from one-seventh of a number y
Thus, for y / 7 - 3 = 9, the final statement is:
"3 subtracted from one-seventh of a number y gives 9".
Q.15. Raju has solved 2 / 4 part of an exercise while Sameer solved 1 / 2 part of it. Who has solved more?
Ans. 2 / 4 part of the exercise is solved by Raju.
When 2 / 4 is converted into lowest form, we get;
►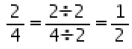
which is the same as part of the exercise solved by Sameer.
Thus, both have solved the same part of the exercise.
Q.16. How many angles are formed when 2 lines intersect?
Ans. When two lines intersect the following figure is formed. This shows that 4 angles are formed.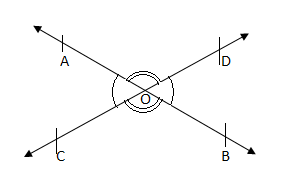 Q.17. How many
Q.17. How many feet long strips of ribbon can be cut from a ribbon that is
feet long strips of ribbon can be cut from a ribbon that is feet long?
feet long?
Ans. Divide the total length of ribbon by the length of each strip of ribbon that is cut from it to get the total number of ribbon strips.
So, divide by
by
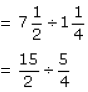
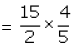
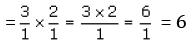
Thus, 6 strips can be cut from the ribbon.
Q.18. If RO is perpendicular to PT, find the measure of angles 1 and 2 in the figure below: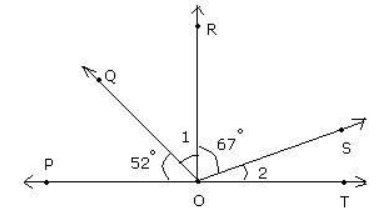 Ans. In the figure, we can see that POR and ROT are right angles.
Ans. In the figure, we can see that POR and ROT are right angles.
Thus, ∠ROS + ∠2 = 90º
∠ROS = 67º
So, ∠2 = 90º - 67º = 23º
Also, ∠POQ + ∠1 = 90º
∠POQ = 52º
So, ∠1 = 90º - 52º = 38º
Q.19. If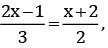 then what is the value of x?
then what is the value of x?
Ans.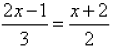
Multiply both sides by 6 (L.C.M of 3 and 2)
► 2 (2x -1) = 3 (x + 2)
► 4x - 2 = 3x + 6
Transpose 3x to L.H.S and -2 to R.H.S
► 4x -3x = 6 + 2 x = 8
Q.20. A Poultry farm produces 600 eggs every week and delivers them equally to 10 shops. The shopkeepers charge Rs.5 for every good egg but they have to give Rs.2 to the customer if the egg comes out to be rotten. A shopkeeper could only earn Rs.276 despite selling all the eggs. How many eggs were rotten?
Ans. Eggs produced by the poultry farm = 600
► Eggs delivered to each shop = 600 ÷ 10 = 60
► Money earned by a particular shopkeeper = Rs. 276
► Money earned if all eggs were good = 60 × 5 = Rs. 300
► Money lost due to rotten eggs = 300 - 276 = Rs. 24
► Cost that shopkeeper will give for one rotten egg = Rs. 2
► Number of rotten eggs = 24 ÷ 2 = 12
► Hence, 12 eggs were rotten.
Q.21. It takes 2 / 5 yards of material to make a shirt. How many yards of material will be required to make 6 shirts?
Ans. Material required to make 1 shirt = 2 / 5 yards
Material required to make 6 shirts = 2 / 5 x 6 = 2 / 5 x 6 / 1 = 12 / 5
Thus, to make 6 shirts, 12 / 5 yards of material will be required.
Q.22. In the figure below, ΔCDE ≅ ΔQPR. What is m ∠D?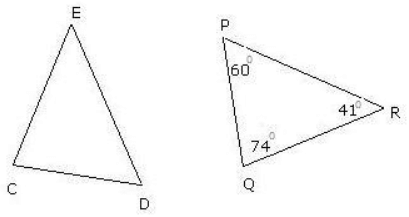 Ans. Given, ΔCDE ≅ ΔQPR We have to find the angle in DPQR that corresponds to ∠D. Now, since corresponding parts of congruent triangles are congruent, ∠D ≅ ∠P.
Ans. Given, ΔCDE ≅ ΔQPR We have to find the angle in DPQR that corresponds to ∠D. Now, since corresponding parts of congruent triangles are congruent, ∠D ≅ ∠P.
Hence, ∠D = 60º.
Q.23. In a cricket match, the runs scored by 11 players are as follows
12, 23, 10, 77, 15, 78, 90, 54, 23, 10, 1
Find the average score.
Ans. Average score = mean score
Mean = Sum of all the observations / Total number of observations
= (12+23+10+77+15+78+90+54+23+10+1)/11
= 393 / 11 = 35.7
Q.24. Explain ASA congruence condition with the help of a diagram.
Ans. ASA congruence criterion:
The Angle Side Angle (ASA) postulate states that, if under a correspondence, two angles and the included side of a triangle is equal to two corresponding angles and the included side of another triangle, then the two triangles are congruent.
Consider the triangles ABC and XYZ, as shown below.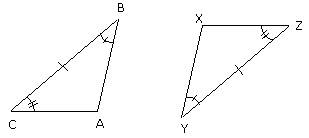 Two angles and the included side are congruent.∠ABC = ∠XYZ (equal angle)BC = YZ (equal side)
Two angles and the included side are congruent.∠ABC = ∠XYZ (equal angle)BC = YZ (equal side)
∠ACB = ∠XZY (equal angle)
So, ABC ≌ XYZ
Therefore, by the ASA congruence criterion, the triangles are congruent.
Section C
Q.25. The bar graph given below shows the sales of books (in thousands) from six branches of a publishing company during two consecutive years 2000 and 2001.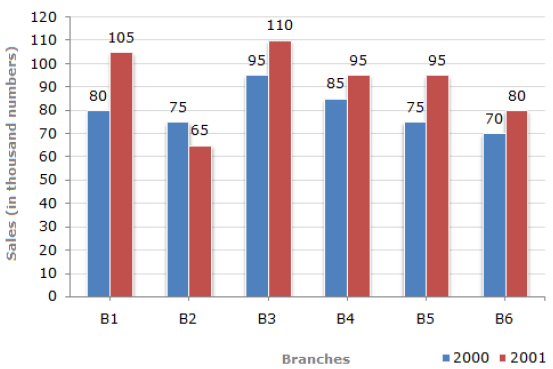
(1) What is the ratio of the total sales of branch B2 for both years to the total sales of branch B4 for both years?
(2) What is the average sale of all the branches (in thousand numbers) for the year 2000
(3) Total sales of branch B6 for both the years is what percent of the total sales of branches B3 for both the years?
Ans. (1) Sales of branch B2 for both years = 75 + 65 = 140
Sales of branch B4 for both years = 85 + 95 = 180
Required ratio = 140 / 180 = 7 / 9 = 7 : 9
(2) Average sales of all the six branches (in thousand numbers) for the year 2000
= 1 / 6 (80 + 75 + 95 + 85 + 75 + 70) = 80
(3) Total sales of branch B6 for both the years = 70 + 80 = 150
Total sales of branch B3 for both the years = 95 + 110 = 205
Required percentage = (150 / 205 x 100)% = 73.17%
Q.26. Let ABC be an isosceles triangle in which AB = AC and BD is perpendicular to AC. Then, prove that BD2 - CD2 = 2AD.CD.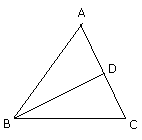 Ans. Since ADB is a right-angled triangle;
Ans. Since ADB is a right-angled triangle;
AD2 + BD2 = AB2
AD2 + BD2 = AC2 [given, AB = AC]
AD2 + BD2 = (AD + CD)2
AD2 + BD2 = AD2 + CD2 + 2AD.CD
[Subtract AD2 from both sides]
BD2 = CD2 + 2AD.CD
[Subtract CD2 from both sides]
BD2 - CD2 = 2AD.CD
Thus, BD2 - CD2 = 2AD.CD
Q.27. Name all the corresponding parts of the congruent figures given below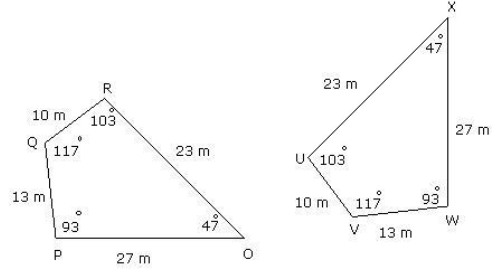 Ans. Given that, both the figures are congruent.
Ans. Given that, both the figures are congruent.
Corresponding sides:
OP ↔ WX; OR ↔ UX; QR ↔ UV; QP ↔ VW
Corresponding vertices:
O ↔ X; P ↔ W; Q ↔ V; R ↔ U
Corresponding angles:
∠O ↔ ∠X ; ∠P ↔ ∠W ; ∠Q ↔ ∠V ; ∠R ↔ ∠U
Q.28. Sumitra has Rs. 34 in denominations of 50 paisa and 25 paisa coins. If the number of 25 paisa coins is twice the number of 50 paisa coins, then how many coins of each type does she has in all?
Ans. Let the number of 50 paisa coins = x
Then, number of 25 paisa coins = 2x
Total money with Sumitra = Rs 34 = 34 × 100 paise = 3400 paise
From the given condition, we have:
► 50x + 25 × 2x = 3400
► 50x + 50x = 3400
100x = 3400 x = 34
Number of 50 paisa coins = 34
Number of 25 paisa coins = 2 × 34 = 68
Q.29. In the figure below, EV, FK and GS are the medians of triangle EFG. Find the values of FS, KG and FV.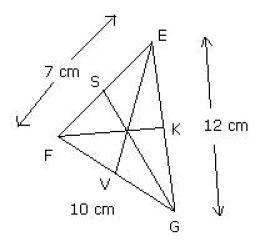 Ans. Given that,
Ans. Given that,
EV, FK and SG are the medians of triangle EFG
Thus K, V and S are the mid-points of EG, FG and EF respectively
Also, given that: EG = 12 cm; FG = 10 cm; EF = 7 cm
Now,
KG =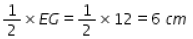
FV =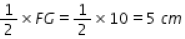
FS =
Thus, the required lengths are
FS = 3.5 cm; KG = 6 cm; FV = 5 cm
Q.30. Two equal sides of a triangle are each 5 less than twice the third side. The perimeter of triangle is 55 m. Find the length of its sides.
Ans. Let the third side = x
Two equal sides are 2x - 5, 2x - 5
Perimeter = Sum of all sides = 55 m
i.e., x + 2x - 5 + 2x - 5 = 55
► 5x - 10 = 55
► 5x = 55 + 10
► 5x = 65 x = 13
Two equal sides = 2x - 5 = 2 × 13 - 5 = 26 - 5 = 21
Thus, the lengths of three sides are 13 m, 21 m and 21 m.
Q.31. Sam's truck gets him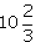 miles per gallon. Suppose the tank is empty and he puts
miles per gallon. Suppose the tank is empty and he puts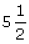 gallons of diesel, how far can Sam go with his truck?
gallons of diesel, how far can Sam go with his truck?
Ans. Distance travelled with 1 gallon
=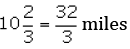
Distance travelled with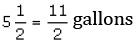
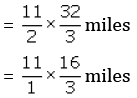
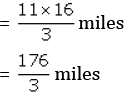
Thus, Sam can go 173 / 3 miles with 11 / 2 gallons.
Q.32. The median of the given data is 29 arranged in increasing order of value. What is the value of x?
x, 20, 2x + 6, 2x + 9, 40, 45, 52
Ans. Median is the middlemost value.
Median = 4th observation = 2x + 9
► 2x + 9 = 29
► 2x = 20
► x = 10
We have to find
[(3x - y + z) + (-y - z)] - (3x - y - z)
= [3x - y + z - y - z] - (3x - y - z)
= (3x - 2y) - (3x - y - z)
= 3x - 2y - 3x + y + z
= 3x - 3x - 2y + y + z = -y + z
Section D
Q.33. A bag has 12 balls colored yellow, blue, green and red. The number of balls of each colour is the same. A ball is drawn from the bag. Calculate the probability of drawing a yellow ball, a blue ball, a green ball and a red ball at the same time. A ball is drawn from the bag. Calculate the probability of drawing a yellow ball, a blue ball, a green ball and a red ball.
Ans. Total number of balls = 12
It is also given that the bag contains an equal number of balls of each of the four colours: yellow, blue, green and red.
Therefore,
► Number of yellow balls = Number of blue balls = Number of green balls = Number of red balls = 3
► P(yellow) = Number of yellow balls / Total number of balls = 3 / 12 = 1 / 4
► P(blue) = Number of blue balls / Total number of balls = 3 / 12 = 1 / 4
► P(green) = Number of green balls / Total number of balls = 3 / 12 = 1 / 4
► P(red) = Number of red balls / Total number of balls = 3 / 12 = 1 / 4
Q.34. A chemist has several beakers full of different liquids that he will use to make a solution. The chemist records the amount of liquid in each beaker: 640.6 millilitres, 908.44 millilitres, 1.5553 litres, and 0.6 litres. How many millilitres of solution will the chemist have after he mixes the liquids in the beakers?
Ans. In order to add the measure of solutions, the amount of liquid in each beaker must have the same units. Since the measures of all the beakers do not have the same units, we convert litres into millilitres to make all the units similar.
We know that:
1 liter = 1000 milliliters
So, 1.5553 liters = 1555.30 milliliters
And 0.6 liters = 600 milliliters
Now, adding all the measurements we get,
Thus, the chemist will get 3704.34 milliliters of the solution after he mixes together the liquids in the beakers.
Q.35. In the figure, O is the midpoint of AQ and BP.
(i) Is ∆OAB ≅ ∆OQP?
(ii) Which pairs of matching parts have you used to answer
(iii) Is AB = PQ?
(iv) Is ∆OAB ≅ ∆OPQ? Solution.
Solution.
(i) Yes
(ii) OA = OQ OB = OP
∆AOB = ∆QOP
(iii) Yes
(iv) No
Q.36. Given data shows the performance of two unit tests.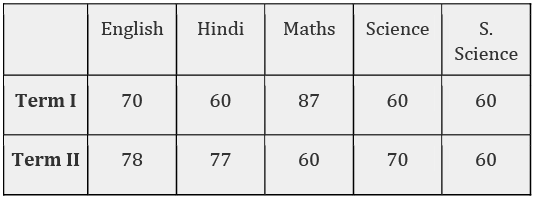 Show the data in a double bar graph.
Show the data in a double bar graph.
Ans. The double bar graph is as shown below: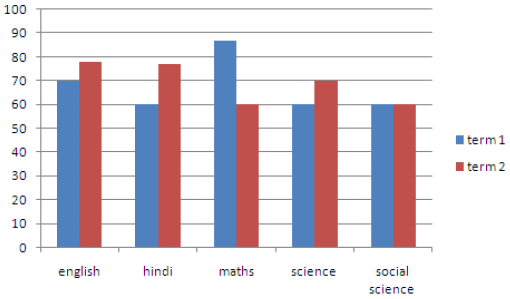
Q.37. In the figure below, AP is parallel to CD. Angle PAB (w) is equal to 135° and angle DCB (z) is equal to 147°. Find angle ABC.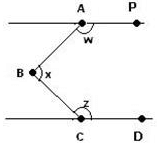 Ans. Draw BS parallel to AP and CD as shown in the figure below.
Ans. Draw BS parallel to AP and CD as shown in the figure below.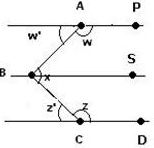 ∠ABC = ∠ABS + ∠CBS∠w' and ∠ABS are alternate interior angles So, ∠ABS = ∠w'∠z' and ∠CBS are alternate interior angles So, ∠CBS = ∠z'
∠ABC = ∠ABS + ∠CBS∠w' and ∠ABS are alternate interior angles So, ∠ABS = ∠w'∠z' and ∠CBS are alternate interior angles So, ∠CBS = ∠z'
► Angles w and w' are supplementary which gives w' = 180º - w = 180º - 135º = 45º
► Angles z and z' are also supplementary which gives z' = 180º - z = 180º - 147º = 33º
Therefore, we have:
∠ABC = ∠ABS + ∠CBS
∠ABC = w' + z' = 45º + 33º = 78º
|
76 videos|344 docs|39 tests
|
FAQs on CBSE Sample Paper Solutions 1 Term 1 - Class 7 Maths
| 1. What is the total duration of the mathematics exam mentioned in the article? |  |
| 2. What is the maximum marks for the mathematics exam mentioned in the article? |  |
| 3. How many sections are there in the mathematics exam mentioned in the article? |  |
| 4. What is the level of the mathematics exam mentioned in the article? |  |
| 5. Is there a sample question paper with solutions available for the mathematics exam mentioned in the article? |  |

|
Explore Courses for Class 7 exam
|

|


















