Ex-18.2 (Part - 1), Surface Area And Volume Of A Cuboid And Cube, Class 9, Math RD Sharma Solutions | RD Sharma Solutions for Class 9 Mathematics PDF Download
Q1) A cuboidal water tank is 6 m long, 5 m wide and 4.5 m deep. How many liters of water can it hold?
Solution:
Given data:
Length (l) = 6m
Breadth (b) = 5m
Height (h) = 4.5m
Volume of the tank = l*b*h
= 6*5*4.5
= 135m3
It is given that,
1m3 = 1000 liters
Therefore,135m3 = (135∗1000)liters
= 135000 liters
The tank can hold 1,35,000 liters of water.
Q2) A cuboidal vessel is 10 m long and 8 m wide. How high must it be made to hold 380 cubic meters of a liquid?
Solution:
Given that
Length of the vessel (l) = 10 m
Width of the Cuboidal vessel = 8 m
Let ‘h’ be the height of the cuboidal vessel.
Volume of the vessel = 380m3
Therefore,l∗b∗h = 380m3
⇒ 10∗8∗h = 380
⇒ h = 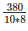
⇒ h = 4.75m
Therefore, height of the vessel should be 4.75 m.
Q3) Find the cost of digging a cuboidal pit 8 m long, 6 m broad and 3 m deep at the rate of Rs 30 per m3
Solution:
Given,
Length of the cuboidal pit (l) = 8 m
Breadth of the cuboidal pit (b) = 6 m
Depth of the cuboidal pit (h) = 3 m
Volume of the Cuboidal pit = l*b*h
= 8*6*3
= 144 m3
Cost of digging 1m3 = Rs. 30
Cost of digging 144m3 = 144*30 = Rs.4320
Q4) If V is the volume of a cuboid of dimensions a, b, c and S is its surface area, then prove that 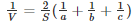
Solution:
Given Data:
Length of the cube (l) = a
Breadth of the cube (b) = b
Height of the cube (h) = c
Volume of the cube (V) = l*b*h
= a*b*c
= abc
Surface area of the cube (S) = 2 (lb+bh+hl)
= 2 (ab+bc+ca)
Now, 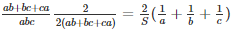
Therefore,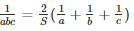
Therefore,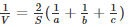
Hence Proved.
Q5) The areas of three adjacent faces of a cuboid are x, y and z.. If the volume is V, Prove that V2 = xyz.
Solution:
Let a, b and d be the length, breadth, and height of the cuboid.
Then, x = ab
y = bc
z = ca
and V = abc [V = l*b*h]
= xyz = ab*bc*ca = (abc)2
and V = abc
V2 = (abc)2
Therefore,V2 = (xyz)
Q6) If the areas of three adjacent face of a cuboid are 8cm3, 18cm3 and 25cm3. Find the volume of the cuboid.
Solution:
WKT, if x, y, z denote the areas of three adjacent faces of a cuboid.
= x = l*b, y = b*h, z = l*h
Volume (V) is given by
V = l*b*h
Now, xyz = lb*bh*hl = V2
Here x = 8
y = 18
z = 25
Therefore,V2 = 8∗18∗25 = 3600
⇒ V = 60cm3
Q7) The breadth of a room is twice its height, one half of its length and the volume of the room is 512 cu. dm. Find its dimensions.
Solution:
Consider l, b and h are the length, breadth and height of the room.
So, b = 2h and b = 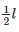
⇒ 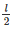 = 2h
= 2h
⇒ l = 4h
⇒ l = 4h,b = 2h
Now, Volume = 512dm3
⇒ 4h∗2h∗h = 512
⇒ h3 = 64
⇒ h = 4
So, Length of the room (l) = 4h = 4*4 = 16 dm
Breadth of the room (b) = 2h = 2*4 = 8 dm
And Height of the room (h) = 4 dm.
Q8) A river 3m deep and 40m wide is flowing at the rate of 2km per hour. How much water will fall into the sea in a minute?
Solution
Radius of the water flow = 2km per hour = 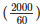 m/min
m/min
= 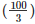 m/min
m/min
Depth of the river (h) = 3m
Width of the river (b) = 40m
Volume of the water flowing in 1 min = 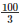 ∗40∗3 = 40003
∗40∗3 = 40003
Thus, 1 minute 4000m3 = 4000000 litres of water will fall in the sea.
Q9) Water in a canal 30dm wide and 12dm deep, is flowing with a velocity of 100km every hour. What much area will it irrigate in 30 minutes if 8cm of standing water is desired?
Solution:
Given that,
Water in the canal forms a cuboid of Width (b) = 30dm = 3m
Height (h) = 12dm = 1.2m
Cuboid length is equal to the distance traveled in 30 min with the speed of 100 km per hour.
Therefore, Length of the cuboid = 100∗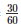 = 60km = 50000metres
= 60km = 50000metres
So, volume of water to be used for irrigation = 5000*3*1.2 m3
Water accumulated in the field forms a cuboid of base area equal to the area of the field and height equal to 8100metres
Therefore,Area of field∗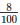 = 50000∗3∗1.2
= 50000∗3∗1.2
⇒ Area of field = 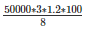
⇒ 22,50,000metres.
Q10) Three metal cubes with edges 6cm, 8cm, 10cm respectively are melted together and formed into a single cube. Find the volume, surface area and diagonal of the new cube.
Solution:
Let ‘a’ be the length of each edge of the new cube.
Then a3 = (63+83+103)cm3
⇒ a3 = 1728
⇒ a = 12
Therefore,Volume of thenewcube = a3 = 1728cm3
Surface area of the new cube = 6a2 = 6∗(12)2 = 864cm2
Diagonal of the newly formed cube = 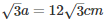
Q11) Two cubes, each of volume 512cm3 are joined end to end. Find the surface area of the resulting cuboid.
Solution:
Given that,
Volume of the cube = 512cm3
⇒ side3 = 512
⇒ side3 = 83
⇒ side = 8cm
Dimensions of the new cuboid formed
Length (l) = 8+8 = 16cm, Breadth (b) = 8cm, Height (h) = 8cm
Surface area = 2(lb+bh+hl)
= 2 (16*8+8*8+16*8)
= 640 cm2
Therefore, Surface area is 640 cm2.
Q12) Half cubic meter of gold-sheet is extended by hammering so as to cover an area of 1 hectare. Find the thickness of the gold-sheet.
Solution:
Given that, Volume of gold-sheet = 0.5m3
Area of the gold-sheet = 1 hectare = 1*10000 = 10000 m2
Therefore,Thickness of gold sheet = 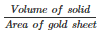
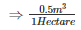
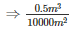
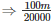
Therefore,Thickness of silve rsheet = 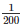 cm
cm
Q13) A metal cube of edge 12cm is melted and formed into three smaller cubes. If the edges of the two smaller cubes are 6cm and 8cm, find the edge of the third smaller cube.
Solution:
Volume of the large cube = v1+v2+v3
Let the edge of the third cube be ‘x’ cm
123 = 63+83+a3 [Volume of cube = side3]
1728 = 216+512+x3
⇒ x3 = 1728−728 = 1000
⇒ x = 10cm
Therefore,Side of thirdside = 10cm
Q14) The dimensions of a cinema hall are 100m, 50m, 18m. How many persons can sit in the hall, if each person requires 150m3 of air?
Solution:
Given that
Volume of cinema hall = 100*50*18 m3
Volume of air required by each person = 150 m3
Number of persons who sit in the hall = 
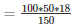 = 600 [Since,V = l×b×h]
= 600 [Since,V = l×b×h]
Therefore, number of persons who can sit in the hall = 600 members.
Q15) Given that 1 cubic cm of marble weighs 0.25kg, the weight of marble block 28cm in width and 5cm thick is 112kg. Find the length of the block.
Solution:
Let the length of the marble block be ‘l’cm
Volume of the marble block = l*b*h cm3
= l*28*5 cm3
Therefore, weight of the marble square = 140l*0.25 kg
As mentioned in the question, weight of the marble = 112 kgs
Therefore,
= 112 = 140l*0.25
= ⇒ l = 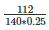 = 3.2cm.
= 3.2cm.
FAQs on Ex-18.2 (Part - 1), Surface Area And Volume Of A Cuboid And Cube, Class 9, Math RD Sharma Solutions - RD Sharma Solutions for Class 9 Mathematics
| 1. How do you find the surface area of a cuboid? |  |
| 2. What is the difference between a cuboid and a cube? |  |
| 3. How do you find the volume of a cube? |  |
| 4. What is the surface area of a cube? |  |
| 5. Can a cuboid and a cube have the same volume? |  |
















