The Ideal Gas Equation, Dalton's Law of Partial Pressures and Mole Fraction | Chemistry for JEE Main & Advanced PDF Download
Ideal Gas Equation
The three gas laws we’ve learned can be combined into a single equation called the ideal gas equation:
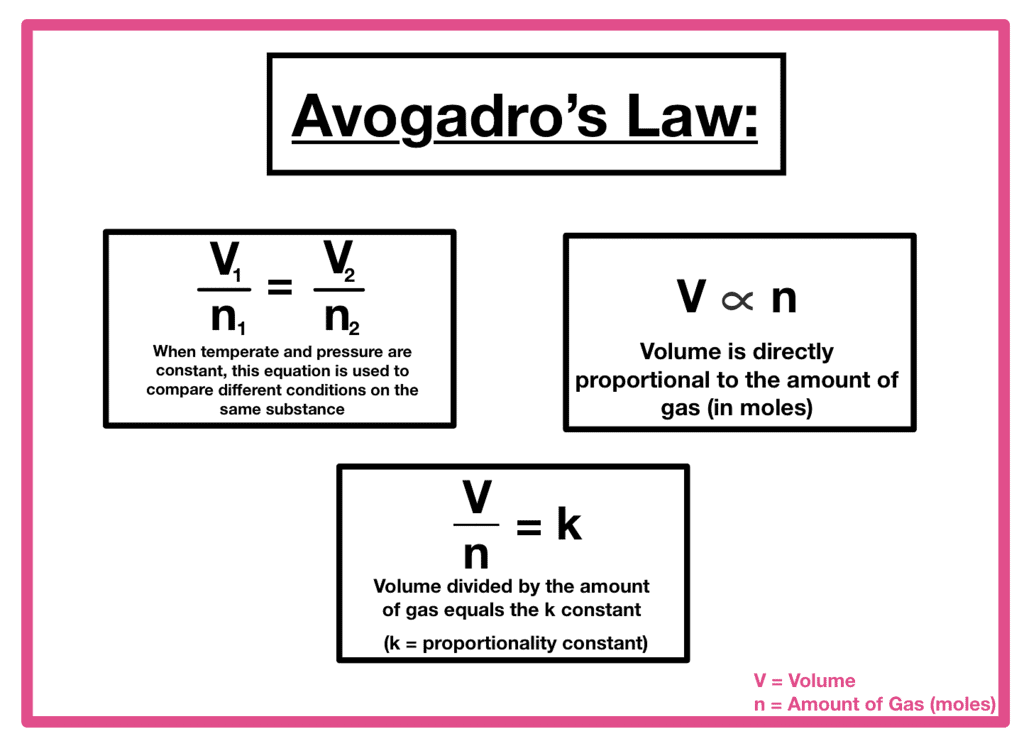
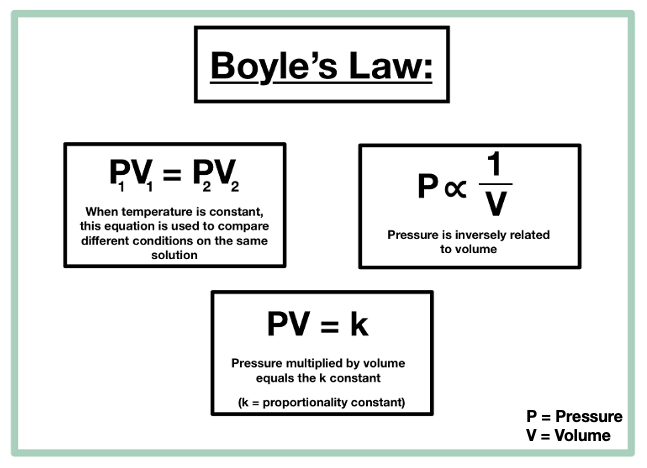
- Boyle’s Law: At constant temperature (T) and moles (n), volume (V) is inversely proportional to pressure (p).

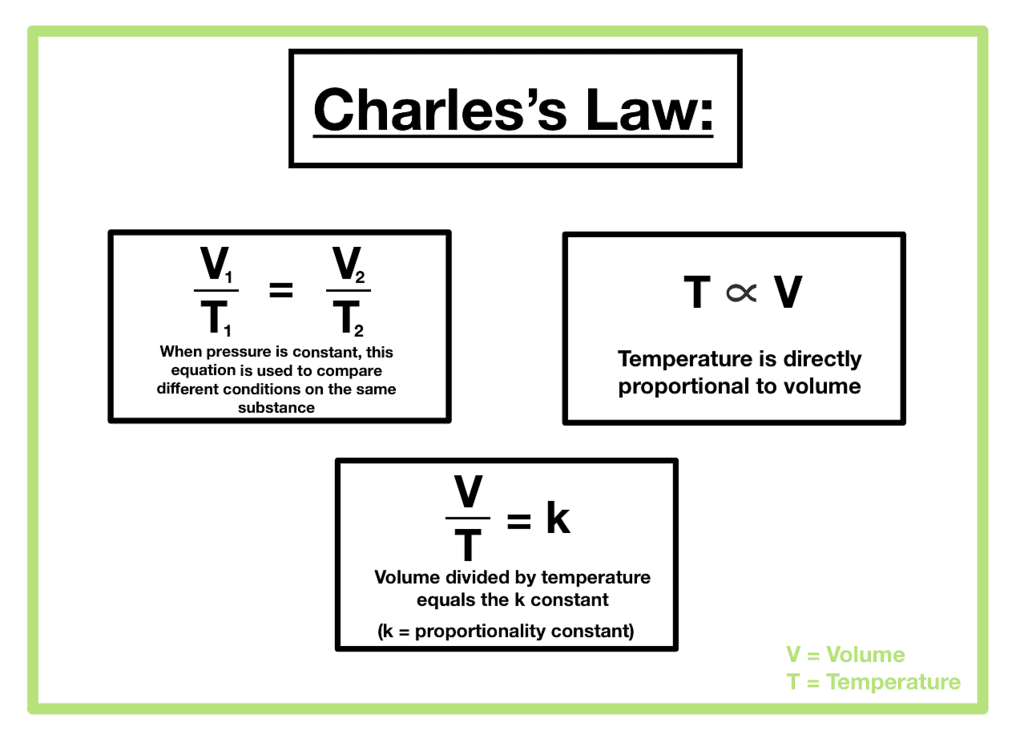
- Charles’ Law: At constant pressure (p) and moles (n), volume (V) is directly proportional to temperature (T).
 Where VI = Initial volume
Where VI = Initial volume
VF = Final volume
TI = Initial absolute temperature
TF = Final absolute temperature - Avogadro’s Law: At constant pressure (p) and temperature (T), volume (V) is directly proportional to the number of moles (n).

Combining these laws, we get:
| PV = nRT |
The state of an ideal gas is determined by the macroscopic and microscopic parameters like pressure, volume, temperature.
Thus, the ideal gas equation is often written as:
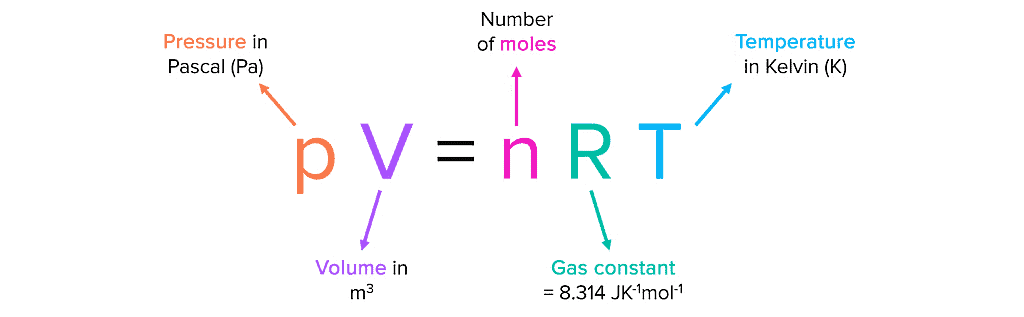
The gas constant R is the same for all gases, so it is called the Universal Gas Constant. The equation pV=nRT is known as the ideal gas equation.
The value of R depends on the units used for pressure (p), volume (V), and temperature (T). If you know any three variables in this equation, you can calculate the fourth. This equation shows that at constant temperature and pressure, n moles of any gas will have the same volume because R, n, T, and p are constant. The ideal gas equation is valid for gases that behave ideally.
At standard temperature and pressure (STP) conditions (273.15 K and 1 bar), the volume of one mole of an ideal gas is 22.710981 L.
The value of R under these conditions can be calculated as follows:
At STP conditions of 0°C and 1 atm pressure,
The ideal gas equation relates four variables and describes the state of any gas, so it is also called the equation of state.
If the temperature, volume, and pressure of a fixed amount of gas change from
Example: An open vessel at 27°C is heated until 3/5th of the air in it has been expelled. Assuming that the volume of the vessel remains constant find
(A) the air escaped out if vessel is heated to 900K.
(B) temperature at which half of the air escapes out.
Solution : One should clearly note the fact that on heating a gas in a vessel, there are the number of moles of gas which go out, the volume of vessel remains constant.
Let initial no. of moles of gas at 300 K be `n'. On heating 3/5 moles of air escape out at temperature T.
Moles of air left at temperature
(A) On heating vessel to 900 K, let n1 moles be left,
n1T1 = n2T2 ⇒ n1
moles escaped out =
moles
(B) Let n/2 moles escape out at temperature T, then
n1 T1 = n2 T2 ⇒
⇒ T = 600 K
Example: 5g of ethane is confined in a bulb of one litre capacity. The bulb is so weak that it will burst if the pressure exceeds 10 atm. At what temperature will the pressure of gas reach the bursting value?
Solution: PV = nRT ⇒ 10 ×1 =
× 0.082 × T
T =
= 60 × 12.18 = 730.81 K = 457.81ºC
Relation between Molecular Mass and Gas Densities
(A) Actual density
For an ideal gas PV = nRT or  , where w = mass of the gas in gms and M = Molecular wt. in gms.
, where w = mass of the gas in gms and M = Molecular wt. in gms.

 or PM = RT, (where is the density of the gas =
or PM = RT, (where is the density of the gas = 


(i) =
=  (for same gas at different temperature and pressure)
(for same gas at different temperature and pressure)
(ii) =
=  (for different gases at same temperature & pressure)
(for different gases at same temperature & pressure)
(Where d = density of gas)
Example: The density of an unknown gas at 98°C and 0.974 atm is 2.5 × 10-3 g/ml. What is the mol wt. of gas?
Solution: Density =
g/ml = 2.5 g/L
PM = ρRT
0.974 × M = 2.5 × 0.0821 × 371
M = 78.18.
(B) Vapour Density
For gases another term which is often used is vapour-density. Vapour density of a gas is defined as the ratio of the mass of the gas occupying a certain volume at a certain temperature and pressure to the mass of hydrogen occupying the same volume at the same temperature and pressure i.e. W (gas) =  .
.
and  mol. wt. of hydrogen is 2)
mol. wt. of hydrogen is 2)

 (Vapour density of gas)
(Vapour density of gas)
Vapour density of a gas is same at any temperature, pressure and volume.
Example: When 3.2 g of sulphur is vapourised at 450°C and 723 mm pressure, the vapours occupy a volume of 780 ml. What is the molecular formula of sulphur vapours under these conditions? Calculate the vapour density also.
Solutlon: PV = nRT ⇒
×
=
× 0.082 × 723
M = 255.9
no. of c atoms of sulpher in one molecule = = 8
Molecular formula of sulphur = S8
V. D. =
=
⇒ 127.99
Dalton's Law of Partial Pressures
John Dalton formulated a law in 1801 that explains how the pressure in a mixture of non-reactive gases works. According to his law, the total pressure of a mixture of gases is the sum of the pressures that each gas would exert if it were alone in the same volume and under the same temperature. The pressure that each individual gas exerts in the mixture is called its partial pressure.

When gases are collected over water, they become moist because they contain water vapor. To find the pressure of the dry gas (without water vapor), you subtract the pressure of the water vapor (called aqueous tension) from the total pressure of the moist gas.
By Dalton's Law,
| PT = P1 + P2 + P3 + ..... |
By the partial pressure of a gas in a mixture is meant, the pressure that the gas will exert if it occupies alone the total volume of the mixture at the same temperature.
Derivation: n = n1 n2 …
 ⇒
⇒  ⇒ P = P1 P2 …
⇒ P = P1 P2 …
Assumption: Volume of all the gases is same as they are kept in same container.
Relationship between Partial Pressure and Number of Moles
The partial pressure of a gas in a mixture can also be expressed in terms of its mole fraction. The mole fraction of a gas is the ratio of the number of moles of that gas to the total number of moles of all gases in the mixture.
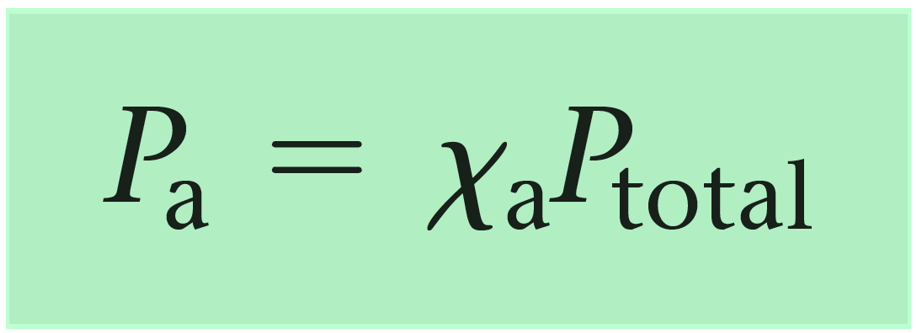
Mathematically, the partial pressure of a gas i ( pi ) can be calculated using its mole fraction ( Xi ) and the total pressure of the gas mixture (p total) 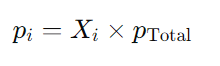
where:
- pi is the partial pressure of gas i.
- Xi is the mole fraction of gas i, which is calculated as Xi= nTotal x ni, where
- ni is the number of moles of gas i and nTotal is the total number of moles of all gases in the mixture.
- pTotal is the total pressure exerted by the mixture of gases.

So, the partial pressure of a gas in a mixture is directly proportional to its mole fraction and the total pressure of the gas mixture.
Important formula
(i)

(ii) Partial pressure of a gas in the mixture
Partial pressure and aqueous tension
Dalton's law is used to calculate the pressure of a dry gas when it is collected over water at atmospheric pressure.
By Dalton's law,
Pressure of dry gas = atmospheric pressure - aqueous tension
Aqueous tension depends on temperature. It increases with temperature and becomes 760 mm at 100°C.
Example: A gaseous mixture contains 55% N2, 20% O2, and 25% CO2 by mass at a total pressure of 760 mm. Calculate the partial pressure of each gas.
Solution: Total mass of the gases = 100 g
= 55g,
= 20 g,
= 25g
= 55/28 = 1.964,
= 20/32 = 0.625,
= 25/44 = 0.568
Total moles = 3.157
Example: A mixture containing 1.6 g of O2, 1.4g of N2 and 0.4 g of He occupies a volume of 10 litre at 27°C. Calculate the total pressure of the mixture and partial pressure of each compound.
Solution: PV = nRT ,where , V = 10 litre , T = 27ºC = 300K
=
= 0.1,
=
= 0.05,
=
= 0.05
Total no. of moles = 0.1 0.05 ⇒ 0.2
PV = nRT ⇒ P× 10 = 0.2 × 0.082 × 300 = 0.04926 ⇒ P = 0.492 atm
Partial pressure = Total pressure × mole fraction
PHe = 0.492 ×
= 0.246 atm
= 0.492 ×
= 0.123 atm
= 0.492 ×
= 0.123 atm
Graham's Law of Diffusion
Diffusion is the tendency of any substance to spread throughout the space available to it. Diffusion will take place in all direction and even against gravity. The streaming of gas molecules through a small hole is called effusion.
According to Graham, the rate of diffusion (or effusion) of a gas at constant pressure and temperature is inversely proportional to the square root of its molecular mass.
 , at constant P and T
, at constant P and T
∴  , at constant P and T
, at constant P and T
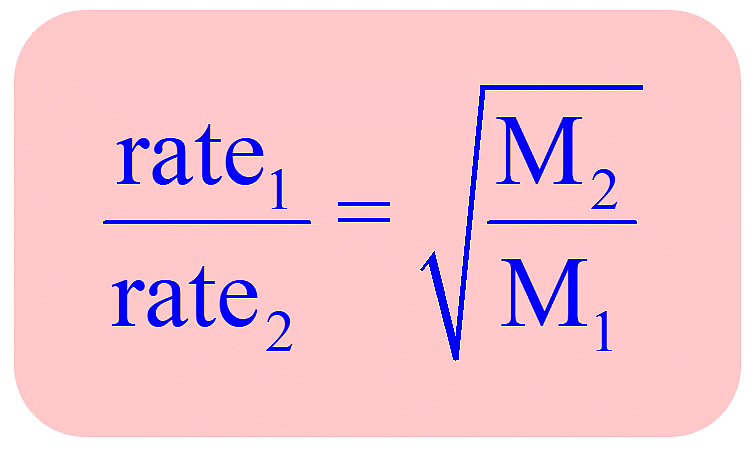
Since molecular mass of gas = 2 × vapour density,  , at constant P and T
, at constant P and T
The rate of diffusion (or effusion) r of two gases under different pressure can be given by
 at constant T only.
at constant T only.


Therefore, according to Graham's law of diffusion (effusion) at constant P and T.

d1 and d2 are the respective densities and V1 and V2 are volumes diffused (effused) in time t1 and t2.

where n1, n2 are moles diffused (effused) in time t1 and t2.

where x1 and x2 are distances travelled by molecules in narrow tube in time t1 and t2.
r =
=
=
Note: It should be noted that the rate of diffusion or effusion actually depends on pressure difference of the gas and not simply on its pressure. Moreover the pressure difference is to be measured for this gas only i.e. if a container holds [He] at a pressure of 0.1 atm and if a small pin-hole is made in the container and if the container is placed in a room, then the rate of effusion of He gas from the container to outside depends only on its pressure difference, which is 0.1-0 (as their is no He in the atmosphere). This implies that the diffusion of a gas is not dependent on the diffusion of any other gas.
Whenever we consider the diffusion of gas under experimental conditions, we always assume that the gas diffuses in vacuum and during the time period for which the diffusion is studied the rate of diffusion (or the composition of diffusing or effusing mixture of gases) remains constant.
Example: Pure O2 diffuses through an aperture in 224 seconds, whereas mixture of O2 and another gas containing 80% O2 diffuses from the same in 234 sec under similar condition of pressure and temperature. What is molecular wt. of gas?
Solution: The gaseous mixture contains 80% O2 and 20% gas.
∴ Average molecular weight of mixture
… (i)
Now for diffusion of gaseous mixture and pure O2
or
… (ii)
∴
By (i) and (ii) mol weight of gas (m) =46.6.
Example: Calculate the relative rates of diffusion of 235UF6 and 238UF6 in the gaseous state (Atomic mass of F = 19).
Solution:
and
(at F = 19)
=
=
= 1.0042.
|
352 videos|596 docs|309 tests
|
FAQs on The Ideal Gas Equation, Dalton's Law of Partial Pressures and Mole Fraction - Chemistry for JEE Main & Advanced
| 1. What is the Ideal Gas Equation and how is it derived? |  |
| 2. How does Dalton's Law of Partial Pressures relate to the Ideal Gas Equation? |  |
| 3. How does molecular mass affect gas densities according to the Ideal Gas Equation? |  |
| 4. What is the significance of Mole Fraction in relation to the Ideal Gas Equation? |  |
| 5. How does Graham's Law of Diffusion relate to the Ideal Gas Equation? |  |
|
352 videos|596 docs|309 tests
|

|
Explore Courses for JEE exam
|

|
 Where VI = Initial volume
Where VI = Initial volume