Chapter 24 - Data Handling-II (Graphical Representation of Data as Histograms) RD Sharma Solutions | RD Sharma Solutions for Class 8 Mathematics PDF Download
Question 1:
Given below is the frequency distribution of the heights of 50 students of a class:
| Class interval: | 140−145 | 145−150 | 150−155 | 155−160 | 160−165 |
| Frequency: | 8 | 12 | 18 | 10 | 5 |
Draw a histogram representing the above data.
Answer 1:
The class limits are represented along the x-axis on a suitable scale and the frequencies are represented along the y-axis on a suitable scale. Taking class intervals as bases and the corresponding frequencies as heights, the rectangles can be constructed to obtain the histogram of the given frequency distribution as shown in the figure below: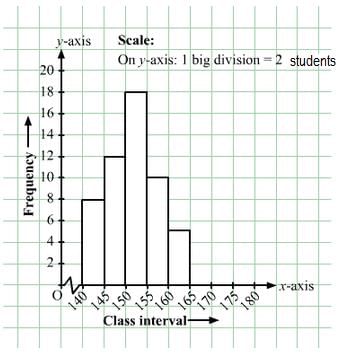
Question 2:
Draw a histogram of the following data:
| Class interval: | 10−15 | 15−20 | 20−25 | 25−30 | 30−35 | 34−40 |
| Frequency: | 30 | 98 | 80 | 58 | 29 | 50 |
Answer 2:
The class limits are represented along the x-axis and the frequencies are represented along the y-axis on a suitable scale. Taking class intervals as bases and the corresponding frequencies as heights, the rectangles can be drawn to obtain the histogram of the given frequency distribution. The histogram is shown below: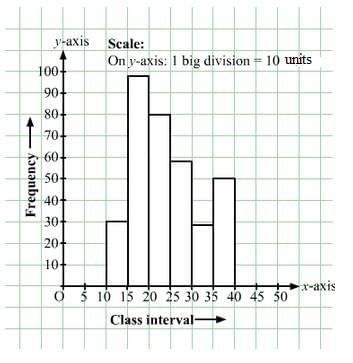
Question 3:
Number of workshops organized by a school in different areas during the last five years are as follows:
| Years | No. of workshops |
| 1995−1996 | 25 |
| 1996−1997 | 30 |
| 1997−1998 | 42 |
| 1998−1999 | 50 |
| 1999−2000 | 65 |
Draw a histogram representing the above data.
Answer 3:
The class limits are represented along the x-axis and the frequencies are represented along the y-axis on a suitable scale. Taking class intervals as bases and the corresponding frequencies as heights, the rectangles can be constructed to obtain histogram for the given frequency. The histogram is shown below: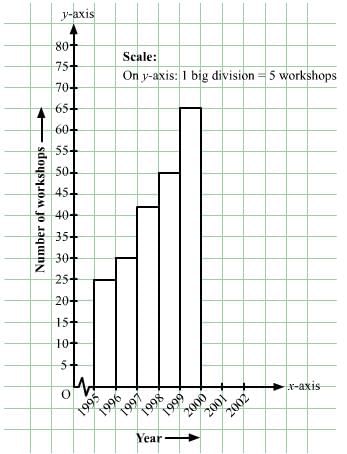
Question 4:
In a hypothetical sample of 20 people the amounts of money with them were found to be as follows:
114, 108, 100, 98, 101, 109, 117, 119, 126, 131, 136, 143, 156, 169, 182, 195, 207, 219, 235, 118.
Draw the histogram of the frequency distribution (taking one of the class intervals as 50−100).
Answer 4:
We first prepare the frequency table for the class intervals 50−100, 100−150,..., 200−250, as shown below:
| Money | Tally Amount | Frequency |
| 50−100 | 98 | 1 |
| 100−150 | 114, 108, 100, 101, 109, 117, 119, 126, 131, 136, 143, 118 | 12 |
| 150−200 | 156, 169, 182, 195 | 4 |
| 200−250 | 207, 219, 235 | 3 |
The class limits are represented along the x-axis and the frequencies along the y-axis on a suitable scale. Taking the class intervals as bases and the corresponding frequencies as heights, the rectangles can be drawn to obtain the histogram of the given frequency distribution. The histogram is shown below: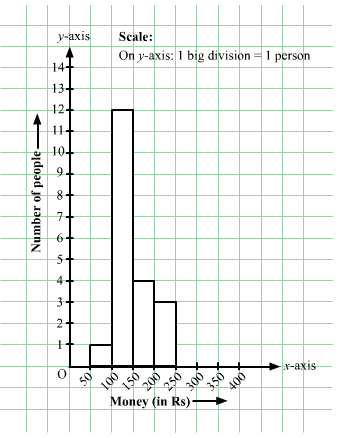
Question 5:
Construct a histogram for the following data:
| Monthly school fee (in Rs): | 30−60 | 60−90 | 90−120 | 120−150 | 150−180 | 180−210 | 210−240 |
| Number of schools: | 5 | 12 | 14 | 18 | 10 | 9 | 4 |
Answer 5:
The class limits are represented along the x-axis and the frequencies along the y-axis on a suitable scale. Taking class intervals as bases and corresponding frequencies as heights of the rectangles, the histogram of the given data can be obtained as shown in the figure below: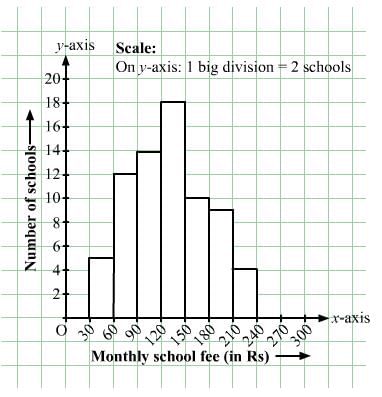
Question 6:
Draw a histogram for the daily earnings of 30 drug stores in the following table:
| Daily earnings (in Rs): | 450−500 | 500−550 | 550−600 | 600−650 | 650−700 |
| Numbers of stores: | 16 | 10 | 7 | 3 | 1 |
Answer 6:
The class limits are represented along the x-axis and the frequencies along the y-axis on a suitable scale. Taking class intervals as bases and the corresponding frequencies as heights, the rectangles can be drawn to obtain the histogram of the given frequency distribution. The histogram is given below: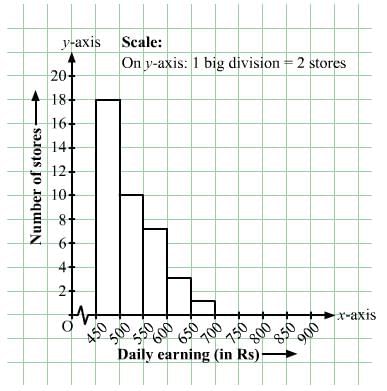
Question 7:
Draw a histogram to represent the following data:
| Monthly salary (in Rs) | Number of teachers |
| 5600−5700 | 8 |
| 5700−5800 | 4 |
| 5800−5900 | 3 |
| 5900−6000 | 5 |
| 6000−6100 | 2 |
| 6100−6200 | 3 |
| 6200−6300 | 1 |
| 6300−6400 | 2 |
Answer 7:
Taking class intervals as bases and the corresponding frequencies as heights, the rectangles can be constructed to obtain the histogram of the given data. The class intervals are represented along the x-axis and the frequencies along the y-axis on a suitable scale.
The histogram representing the given data is shown below: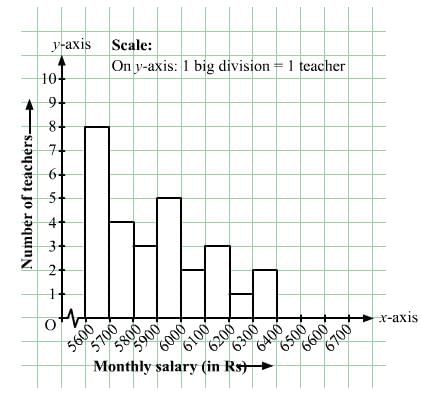
Question 8:
The following histogram shows the number of literate females in the age group of 10 to 40 years in a town: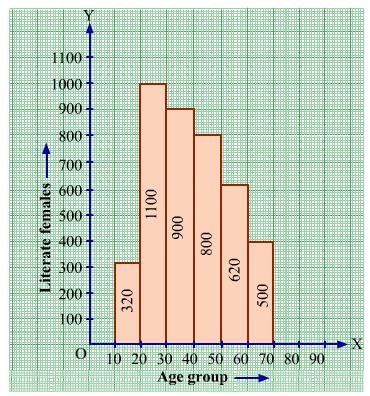
(i) Write the age group in which the number of literate female is the highest.
(ii) What is the class width?
(iii) What is the lowest frequency?
(iv) What are the class marks of the classes?
(v) In which age group literate females are the least?
Answer 8:
(i) The highest rectangle corresponds to the highest number of literate females, which is in the interval 15−20 years.
(ii) The class intervals are 10−15, 15−20, 20−25, 30−35, 35−40. Hence, the class width is 5.
(iii) The lowest rectangle corresponds to the lowest frequency, which is 320.
(iv) The class mark is the mid-point of the class interval.
class mark = 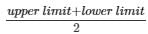
Hence, the class mark of each class is as follows:
| Interval | Class Mark |
| 10−15 | 12.5 |
| 15−20 | 17.5 |
| 20−25 | 22.5 |
| 25−30 | 27.5 |
| 30−35 | 32.5 |
| 35−40 | 37.5 |
(v) The lowest rectangle corresponds to the least number of literate females, which is in the interval 10−15 years.
Question 9:
The following histogram shows the monthly wages (in Rs) of workers in a factory: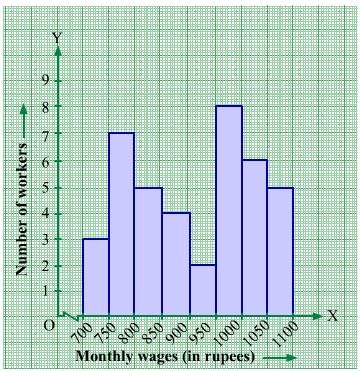
(i) In which wage-group the largest number of workers are being kept? What is their number?
(ii) What wages are the least number of workers getting? What is the number of such workers?
(iii) What is the total number of workers?
(iv) What is the factory size?
Answer 9:
(i) In Fig 24.8, the highest rectangle corresponds to the largest number of workers. The required interval is Rs 950−1000. There are 8 workers in this interval.
(ii) The lowest rectangle corresponds to the least number of workers. The required interval is Rs 900−950. There are 2 workers in this interval.
(iii) The total number of workers is the sum of workers in all the intervals. It can be calculated as follows:
Total workers = 3 + 7 + 5 + 4 + 2 + 8 + 6 + 5 = 40 workers
(iv) The factory intervals are 750−800, 800−850, .. 1050−100. Hence, the factory size is 50.
Question 10:
Below is the histogram depicting marks obtained by 43 students of a class:
(i) Write the number of students getting the highest marks.
(ii) What is the class size?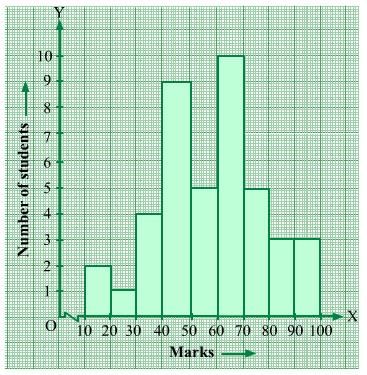
Answer 10:
(i) In the given histogram, the interval with the highest marks is 90−100.
Three students are there in this interval because the height of the rectangle (90−100) is 3 units.
(ii) The class intervals are 10−20, 20−30, ..., 90−100. So, the class size is 10.
Question 11:
The following histogram shows the frequency distribution f the ages of 22 teachers in a school:
(i) What is the number of eldest and youngest teachers in the school?
(ii) Which age group teachers are more in the school and which least?
(iii) What is the size of the classes?
(iv) What are the class marks of the classes?
Answer 11:
(i) The eldest (50−55 years) = 1 person
This is because the height of the rectangle with class interval 50−55 as base is 1 unit.
The youngest (20−25 years) = 2 persons
This is because the height of the rectangle with class interval 20−25 as base is 2 units.
(ii) The group containing the most number of teachers is 35−40 years. This is because the height of the rectangle with class interval 35−40 as base is the maximum.
The group containing the least number of teachers is 50−55 years. This is because the height of the rectangle with class interval 50−55 as base is the minimum.
(iii) Class size = The range between the upper and the lower boundaries of the class
For example, the size of the class 20−25 years is 5.
(iv) Class mark = 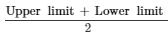
For class 20−25:Class mark = 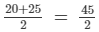 = 22.5
= 22.5
Similarly, the class marks of the other classes are 27.5; 32.5; 37.5; 42.5; 47.5; 52.5.
Question 12:
The weekly wages (in Rs.) of 30 workers in a factory are given:
830, 835, 890, 810, 835, 836, 869, 845, 898, 890, 820, 860, 832, 833, 855, 845, 804, 808, 812, 840, 885, 835, 835, 836, 878, 840, 868, 890, 806, 840
Mark a frequency table with intervals as 800-810, 810-820 and so on, using tally marks. Also, draw a histogram and answer the following questions:
(i) Which group has the maximum number of workers?
(ii) How many workers earn Rs 850 and more?
(iii) How many workers earn less than Rs 850?
Answer 12:
The frequency table with intervals 800−820, 810−820,...890−900 is given below:
| Wage (in Rs) | Tally Wage | Frequency | Tally marks |
| 800−810 | 804, 808, 806 | 3 | III |
| 810−820 | 810, 812 | 2 | II |
| 820−830 | 820 | 1 | I |
| 830−840 | 830, 835, 835, 836, 832, 833, 835, 835, 836 | 9 | IIII IIII |
| 840−850 | 845, 845, 840, 840, 840 | 5 | IIII |
| 850−860 | 855 | 1 | I |
| 860−870 | 869, 860, 868 | 3 | III |
| 870−880 | 878 | 1 | I |
| 880−890 | 885 | 1 | I |
| 890−900 | 890, 898, 890, 890 | 4 | IIII |
The class limits are represented along the x-axis and the frequencies along the y-axis on a suitable scale. Taking class intervals as bases and the corresponding frequencies as heights, the rectangles can be drawn to obtain the histogram of the given frequency distribution. The histogram is shown below: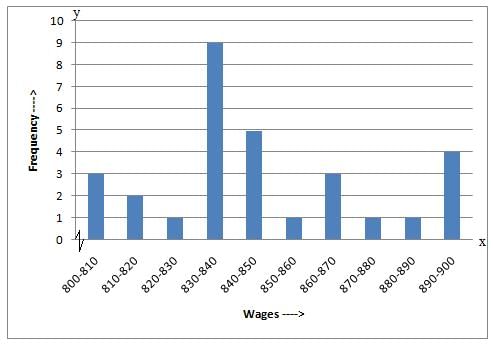
(i) The group that has the maximum number of workers is represented as the highest rectangle. It is in the interval 830−840.
(ii) The number of workers who earn Rs 850 or more can be calculated from frequency table in the following manner:
1 + 3 + 1 + 1 + 4 = 101 + 3 + 1 + 1 + 4 = 10
(iii) The number of workers who earn less than Rs 850 can be calculated from frequency table in the following manner:
3 + 2 + 1 + 9 + 5 = 203 + 2 + 1 + 9 + 5 = 20
FAQs on Chapter 24 - Data Handling-II (Graphical Representation of Data as Histograms) RD Sharma Solutions - RD Sharma Solutions for Class 8 Mathematics
| 1. What is a histogram and how is it used to represent data? |  |
| 2. How do you construct a histogram from a given data set? |  |
| 3. What information can be obtained from a histogram? |  |
| 4. How can a histogram be used for data analysis and interpretation? |  |
| 5. What are the advantages of using a histogram to represent data? |  |





















