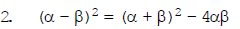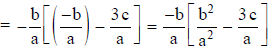Factorisation of Polynomials and Factor Theorem - Polynomials, Class 9, Mathematics PDF Download
FACTOR THEOREM
If p(x) is a polynomial of degree n ≥ 1 and a is any real number, then
(i) x – a is a factor of p(x), then p(a) = 0 and
(ii) p(a) = 0 then x – a is a factor of p(x).
|
REMARK
|
Ex. Use the factor theorem to determine whether x – 1 is a factor of
(a) x3 + 8x2 – 7x – 2
(b) 2√2 x3 + 5√2 x2 – 7√2
Sol. (a) Let p(x) = x3 + 8x2 – 7x – 2
By using factor theorem, (x – 1) is a factor of p(x) only when p(1) = 0
p(1) = (1)3 + 8(1)2 – 7(1) – 2 = 1 + 8 – 7 – 2 = 9 – 9 = 0
Hence (x – 1) is a factor of p(x).
(b) Let p(x) = 2√2x3 + 5√2x2 – 7√2
By using factor theorem, (x – 1) is a factor of p(x) only when p(1) = 0
p(1) = 2√2 (1)3 + 5√2 (1)2 – 7√2 = 2√2 + 5√2 – 7√2 = 7√2 – 7√2 = 0
Hence (x – 1) is a factor of p(x).
Ex. Without actual division, prove that the polynomial 2x3 + 13x2 + x – 70 is exactly divisible by x – 2.
Sol. The polynomial p(x) = 2x3 + 13x2 + x – 70 is exactly divisible by x – 2 means that x – 2 is a factor of
p(x) = 2x3 + 13x2 + x – 70.
Now p(2) =2(2)3 + 13(2)2 + 2 – 70 = 16 + 52 + 2 – 70 = 0
∴ By factor theorem, x – 2 is a factor of p(x)
i.e. p(x) = 2x3 + 13x2 + x – 70 is exactly divisible by x – 2.
FACTORISING OF POLYNOMIAL OF HIGHER DEGREE
- Obtain the polynomial p(x)
- Obtain the constant term in p(x) and find its all possible factors. For example, in the polynomial x4 + x3 – 7x2 – x + 6 the constant term is 6 and its factors are ±1, ±2, ±3, ±6.
- Take one of the factors, say a and replace x by it in the given polynomial. If the polynomial reduces to zero, then (x – a) is a factor of polynomial.
- Obtain the factors equal in number to the degree of polynomial. Let these are (x – a), (x – b), (x – c). ....
- Write p(x) = k (x – a) (x – b) (x – c) ..... where k is constant.
- Substitute any value of x other than a, b, c .......... and find the value of k.
Ex. Using factor theorem, factorize the polynomial x3 – 6x2 + 11x – 6.
Sol. Let f(x) = x3 – 6x2 + 11x – 6
The constant term in f(x) is equal to –6 and factors of – 6 are ±1, ±2, ±3, ±6. Putting x = 1 in f(x), we have
f(1) = (1)3 – 6 × (1)2 + 11 × 1 – 6 = 1 – 6 + 11 – 6 = 0 ∴ (x – 1) is a factor of f(x)
Similarly, x – 2 and x – 3 are factors of f(x). Since f(x) is a polynomial of degree 3. So, it can not have more than three linear factors.
Let f(x) = k (x – 1) (x – 2) (x – 3)
Then,x3 – 6x2 + 11x – 6 = k(x – 1) (x – 2) (x – 3)
Putting x = 0 on both sides, we get – 6 = k (0 – 1) (0 – 2) (0 – 3) ⇒ –6 = – 6 k ⇒ k = 1
Putting k = 1 in f(x) = k(x – 1) (x – 2) (x – 3), we get f(x) = (x – 1) (x – 2) (x – 3)
Hence, x3 – 6x2 + 11x – 6 = (x – 1) (x – 2) (x – 3)
Ex. Using factor theorem, factorize the polynomial x4 + x3 – 7x2 – x + 6.
Sol. Let f(x) = x4 + x3 – 7x2 – x + 6 the factors of constant term 6 are ±1, ±2, ±3 and ±6
Now, f(1) = 1 + 1 – 7 – 1 + 6 = 8 – 8 = 0
⇒ (x – 1) is a factor of f(x)
f(–1) = 1 – 1 – 7 + 1 + 6 = 8 – 8 = 0 ⇒ (x + 1) is a facor of f(x)
f(2) = 24 + 23 – 7 × 22 – 2 + 6 = 16 + 8 – 28 – 2 + 6 = 0
⇒ x – 2 is a factor of f(x)
f(–2) = (–2)4 + (–2)3 – 7(–2)2 – (–2) + 6 = 16 – 8 – 28 + 2 + 6 = – 12 ≠ 0
⇒ x + 2 is not a factor of f(x)
f(–3) = (–3)4 + (–3)3 – 7(–3)2 – (–3) + 6 = 81 – 27 – 63 + 3 + 6 = 90 – 90 = 0
⇒ x + 3 is a factor of f(x).
Since f(x) is a polynomial of degree 4. So, it cannot have more than 4 linear factors
Thus, the factor of f(x) are (x – 1), (x + 1), (x – 2) and (x + 3).
Let f(x) = k(x – 1) (x + 1) (x – 2) (x + 3)
⇒ x4 + x3 – 7x2 – x + 6 = k (x – 1) (x + 1) (x – 2) (x + 3) ... (i)
Putting k = 0 on both sides, we get
6 = k (–1) (1) (–2) (3) ⇒ 6 = 6 k ⇒ k = 1
Substituting k = 1 in (i), we get
x4 + x3 – 7x2 – x + 6 = (x – 1) (x + 1) (x – 2) (x + 3)
|
COMPETITION WINDOW ZERO OF A QUADRATIC POLYNOMIAL Some useful relations involving α and β :
Ex. If α and β are the zeroes of the polynomial ax2 + bx + c. Find the value of (ii) α2 + β2 (i) (α – β)2 = (α + β)2 – 4αβ (ii) α2 + β2 = α2 + β2 + 2αβ – 2αβ = (α + β)2 – 2αβ Ex. If α and β are the zeroes of the quadratic polynomial ax2 + bx + c. Find the value of (i) α2 – β2 (ii) α3 + β3. (i) α2 – β2 = (α + β) (α – β) (ii) α3 + β3 = (α + β) (α2 + β2 – αβ) = (α + β) [(α2 + β2 + 2αβ) – 3αβ] = (α + β) [(α + β)2 – 3αβ] =
TO FORM A QUADRATC POLYNOMIAL WITH THE GIVEN ZEROES Let the zeroes of a quadratic polynomial be α and β. Ex. Form the quadratic polynomial whose zeroes are 4 and 6. Ex. Form the quadratic polynomial whose zeroes are –3, 5 |
FAQs on Factorisation of Polynomials and Factor Theorem - Polynomials, Class 9, Mathematics
| 1. What is a polynomial? |  |
| 2. What is factorisation of polynomials? |  |
| 3. What is the Factor Theorem? |  |
| 4. How do you factorise a quadratic polynomial? |  |
| 5. What are the practical applications of factorisation of polynomials? |  |