Exponents and Powers Class 7 Notes Maths Chapter 10
| Table of contents |

|
| Introduction |

|
| What are Exponents? |

|
| Laws of Exponents |

|
| Miscellaneous Examples Using The Laws Of Exponents |

|
| Decimal Number System |

|
| Expressing Large Numbers in the Standard Form |

|
Introduction
Large numbers can often be difficult to read, understand, and compare. For instance:
- The Earth's mass is approximately 5,970,000,000,000,000,000,000,000 kg.
- Uranus’s mass is about 86,800,000,000,000,000,000,000,000 kg.
Similarly, we can compare the distances:
- The distance between the Sun and Saturn is 1,433,500,000,000 meters.
- The distance between Saturn and Uranus is 1,439,000,000,000 meters.
Dealing with such massive numbers can be overwhelming. To simplify this, we use exponents, which help express and understand large numbers in a more compact and manageable form.
What are Exponents?
Exponents are a way to express very large or very small numbers in a more compact and manageable form, making it easier to read, understand, and compare them.

Exponents provide a shorthand way to express both very large and very small numbers. When a number is multiplied by itself multiple times, we use exponents to represent this repeated multiplication.
For example:
- (read as “8 raised to the power of 3”) equals 512. Here, 8 is the base, and 3 is the exponent. The number is the exponential form of 512.

- can be written as 0×10×10=104
Here are some Basic Terms related to Exponents and Powers
1. Base and Exponent
In 10³, 10 is the base and 3 is the exponent.
- The base represents the number being multiplied, and the exponent indicates how many times the base is multiplied by itself.
2. Expressing Numbers in Expanded Form
Numbers can also be expanded using exponents:

- Example: 47561 can be written as 4 × 10⁴ + 7 × 10³ + 5 × 10² + 6 × 10¹ + 1.
- Practice with numbers like 172, 5642, and 6374.
3. Exponents with Bases Other Than 10
Exponents work with any base, not just 10.
Example: 81 = 3 × 3 × 3 × 3 = 3⁴.
4. Special names for powers:
- 10² = "10 squared"
- 10³ = "10 cubed"
- Example: 5³ = 5 × 5 × 5 = 125 (125 is the third power of 5).
5. Exponents with Negative Bases
Negative integers can also have exponents.
- Example: (–2)³ = (–2) × (–2) × (–2) = –8.
- (–2)⁴ = 16, as even powers of negative numbers yield positive results.
6. General Exponent Rule
For any integer a, the powers are:
- a² = a × a
- a³ = a × a × a
- a⁴ = a × a × a × a, and so on.
- Example: a³b² = a × a × a × b × b.
7. Prime Factorization Using Exponents
Prime factorization is a method used to express a number as the product of its prime factors. Using exponents in prime factorization simplifies the representation by indicating how many times a prime factor appears.
 Prime Factors Examples
Prime Factors Examples
Express numbers as a product of prime factors.
- 72 = 2³ × 3².
- 432 = 2⁴ × 3³.
- 1000 = 2³ × 5³.
- 16,000 = 2⁷ × 5³.
Below are some examples of Using Exponents
Example 1: Express 256 as a power of 2.
256 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 = 2⁸.
Example 2: Which is greater, 2³ or 3²?
2³ = 8, 3² = 9. Since 9 > 8, 3² is greater.
Example 3: Which is greater, 8² or 2⁸?
8² = 64, 2⁸ = 256. Clearly, 2⁸ > 8².
Example 4: Express the following numbers as a product of powers of prime factors:
(i) 432
Ans: 432 = 2 × 216 = 2 × 2 × 108 = 2 × 2 × (2 × 54) = 2 × 2 × 2 × 2 × 27
= 2 × 2 × 2 × 2 × 3 × 9
= 2 × 2 × 2 × 2 × 3 × 3 × 3 or 432
= 24 × 33
(ii) 16000
Ans:16,000 = 16 × 1000 = (2 × 2 × 2 × 2) ×1000 = 24 ×103
(as 16 = 2 × 2 × 2 × 2)
= (2 × 2 × 2 × 2) x (2 × 2 × 2 × 5 × 5 × 5)
= 24 × 23 × 53
(Since 1000 = 2 × 2 × 2 × 5 × 5 × 5)
= (2 × 2 × 2 × 2 × 2 × 2 × 2 ) × (5 × 5 × 5) or, 16,000
= 27 × 53
Example 5: Expand a3b2, a2b3, b2a3, b3a2 . Are they all same?
Ans: a3b2 = a3 × b2 = (a × a × a) × (b × b) = a × a × a × b × b
a2b3 = a2 x b3 = (a × a) × (b × b × b)
b2a3 = b2 × a3 = (b × b) × (a × a × a)
b3a2 = b3 x a2 = (b × b × b) × (a × a)
In the terms a3b2 and a2b3 the powers of a and b are different. Thus a3b2 and a2b3 are different. On the other hand, a3b2 and b2a3 are the same, since the powers of a and b in these two terms are the same. The order of factors does not matter. Thus, a3b2 = a3× b2 = b2 × a3 = b2a3
Similarly, a2b3 and b3a2 are the same.
Laws of Exponents
Exponent rules, which are also known as the 'Laws of Exponents' or the 'Properties of Exponents' make the process of simplifying expressions involving exponents easier. These rules are helpful to simplify the expressions that have decimals, fractions, irrational numbers, and negative integers as their exponents.
Example: if we need to solve 34 × 32, we can easily do it using one of the exponent rules which says, am× an = am + n.
Using this rule, we will just add the exponents to get the answer, while the base remains the same, that is, 34 × 32 = 34 + 2 = 36
Similarly, expressions with higher values of exponents can be conveniently solved with the help of the exponent rules.
Here is the list of exponent rules.

- Multiplying Powers with the Same Base: For any non-zero integer a and whole number m and n, am × an = am+n.
Example: let us multiply 22 × 23. Using the rule, 22 × 23 = 2 (2 + 3) = 25.
- Dividing Powers with the Same Base :
For any non-zero integer a and whole number m and n (m > n), am ÷ an = am-n
Example: 56 / 52 = = 5 × 5 × 5 × 5 = 56-2
= 5 × 5 × 5 × 5 = 56-2 
- Taking Power of a Power :
For any non-zero integer a and whole number m and n, (am)n = amn
Example: (32)4 = 32 × 32 × 32 × 32 = 3(2+2+2+2) = 38 = 32 × 4
(8 is the product of 2 and 4) - Multiplying Powers with the Same Exponents :
For any non-zero integers a and b and whole number m, am × bm = (ab)m
Example: 23 × 33 = (2 × 2 × 2) × (3 × 3 × 3) = (2 × 3) × (2 × 3) × (2 × 3) = 6 × 6 × 6 = 63
In general, for any non-zero integer am × bm = (ab)m (where m is any whole number) - Dividing Powers with the Same Exponents :
For any non-zero integers a and b and whole number m, am ÷ bm = am/bm = (a/b)m
Example:
We may generalize (am/bm) = where a and b are any non-zero integers and m is a whole number.
where a and b are any non-zero integers and m is a whole number.
Example: Simplify the expression by using the laws of exponents: 10-3 × 104
Solution: According to the exponent rules, to multiply two expressions with the same base, we add the exponents while the base remains the same. This means, 10-3 × 104 = 10(-3 + 4) = 101 = 10
Example: Simplify the given expression and select the correct option using the laws of exponents: 1015 ÷ 107
(a) 108
(b) 1022
Solution:
As per the exponent rules, when we divide two expressions with the same base, we subtract the exponents. This means, 1015/107= 1015 - 7 = 108. Therefore, the correct option is (a) 108
(a) If a fraction has a negative exponent, then we take the reciprocal of the fraction to make the exponent positive, i.e., (a/b)-m = (b/a)m
(b) 6720 = 0
Solution:(a) True, if a fraction has a negative exponent rule, then we take the reciprocal of the fraction to make the exponent positive, i.e., (a/b)-m = (b/a)m
(b) False, according to the zero rule of exponents, any number to the power of zero is always equal to 1. So, 6720 = 1
Answer: (a) True (b) False
Miscellaneous Examples Using The Laws Of Exponents
Q.1. Write exponential form for 8 × 8 × 8 × 8 taking base as 2.
Sol: 
Q.2. Simplify and write the answer in the exponential form. 
Sol: 
Q.3. Simplify and write the answer in the exponential form 
Sol: 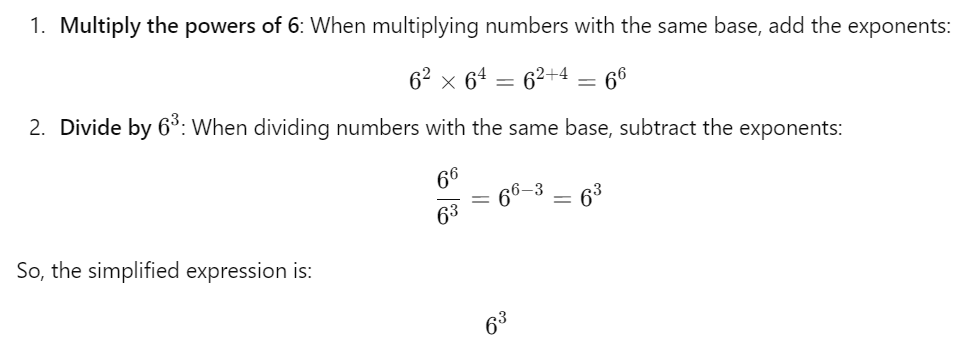
Decimal Number System
A number expressed in decimal notation is written as a single number made up of integer digits in the units, tens, hundreds, thousands, et cetera positions to the left of the decimal point and possibly also in the tenths, hundredths, and so on to the right of the decimal point.
 Let's understand this by writing number 4872 in expanded form using powers of 10:
Let's understand this by writing number 4872 in expanded form using powers of 10:
4872 =4000+800+70+2 = 4×1000 + 8×100 + 7×10 + 2×1
4872 = ( 4×103 )+( 8×102 )+( 7×101 )+( 2×100 )
= 4872
Expressing Large Numbers in the Standard Form
Any number can be expressed as a decimal number between 1.0 and 10.0
(including 1.0) multiplied by a power of 10. Such a form of a number is called its standard form or scientific notation.

For example:
Speed of light in vacuum = 300000000 m/s = 3.0 × 108 m/s.
The distance between the Sun and Earth is 149, 600,000,000 m = 1.496 × 1011m.
Example: Express the following numbers in the standard form:
(i) 5985.3
Ans: 5985.3 = 5.9853 × 1000 = 5.9853 × 103
(ii) 70,040,000,000
Ans: 70,040,000,000 = 7.004 × 10,000,000,000 = 7.004 × 1010
Example: Solve the following
(i) 23 x 22
Ans: Numbers raised to the power of three are called cube numbers From the law of exponent
we know, pm x pn =p(m+n)
Therefore, 23 x 22 = 2(3+2) = 25 = 2 x 2 x 2 x 2 x 2 = 32
(ii) (52)2
Ans: We know, by the law of exponent,
(pm)n = pmn
Therefore, (52)2 = 5 2x2 = 54 = 625
(iii) (53 × 54) / 52
Ans: Using the law of exponents, we know that am × an = a(m+n)
⇒ 53 × 54 = 5(3+4) = 57
Now, we have (57) / 52
Using the law of exponents, we know that am / an = a(m-n)
⇒ 57 / 52 = 5(7-2) = 55
So, the simplified expression is 55.
|
76 videos|344 docs|39 tests
|
FAQs on Exponents and Powers Class 7 Notes Maths Chapter 10
| 1. What are exponents and how are they used in mathematics? |  |
| 2. What are the laws of exponents? |  |
| 3. How can we express large numbers in standard form? |  |
| 4. What are some examples of using the laws of exponents in calculations? |  |
| 5. Why is the decimal number system important in relation to exponents? |  |

|
Explore Courses for Class 7 exam
|

|


 = 5 × 5 × 5 × 5 =
= 5 × 5 × 5 × 5 = 

 where a and b are any non-zero integers and m is a whole number.
where a and b are any non-zero integers and m is a whole number.

















