कैलेंडर का सिद्धांत | General Intelligence & Reasoning for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA PDF Download

कैलेंडर आधारित प्रश्नों का महत्व
\"कैलेंडर\" विषय का अध्ययन प्रतियोगी परीक्षाओं में तार्किक तर्क के लिए अत्यंत महत्वपूर्ण है क्योंकि इसमें जटिल तार्किक विश्लेषण शामिल होता है, जो समस्या-समाधान कौशल को बढ़ाता है। प्रतियोगी परीक्षाओं में सामान्यतः 2 से 4 प्रश्न आते हैं, इसलिए कैलेंडर के सिद्धांतों की मजबूत समझ होना स्कोर को अधिकतम करने के लिए आवश्यक है। इसके अतिरिक्त, इसमें गणितीय अवधारणाओं का उपयोग करना भी आवश्यक है, जो इसे तार्किक तर्क की तैयारी का एक बहुपरक और महत्वपूर्ण घटक बनाता है।

कैलेंडर क्या है?

कैलेंडर एक चार्ट या पृष्ठों की श्रृंखला है जो किसी विशेष वर्ष के दिनों, हफ्तों और महीनों को दर्शाती है, या विशेष मौसमी जानकारी देती है।

कैलेंडर की मूल संरचना

• साधारण वर्ष: कोई भी वर्ष जिसमें 365 दिन होते हैं, उसे साधारण वर्ष कहा जाता है। उदाहरण: 1879, 2009, 2019 आदि।
• लीप वर्ष: कोई भी वर्ष जिसमें 366 दिन होते हैं, उसे लीप वर्ष कहा जाता है। उदाहरण: 2012, 2016, 2020 आदि।
• संख्या 365 को 7 से विभाजित करने पर भागफल 52 और शेष 1 मिलता है, जो दर्शाता है कि एक साधारण वर्ष में 52 सप्ताह और एक अतिरिक्त दिन होता है। इस अतिरिक्त दिन को कैलेंडर विषयों में “अजीब दिन” कहा जाता है।
• लीप वर्ष में 366 दिन होते हैं, संख्या 366 को 7 से विभाजित करने पर भागफल 52 और शेष 2 मिलता है। यह दर्शाता है कि एक लीप वर्ष में 52 सप्ताह और 2 अजीब दिन होते हैं। इन दो अतिरिक्त दिनों को भी “अजीब दिन” कहा जाता है।

अजीब दिनों की अवधारणा

1. एक महीने में अजीब दिनों की संख्या

• जनवरी में 31 दिन होते हैं, चाहे वह साधारण वर्ष हो या लीप वर्ष। संख्या 31 को 7 से विभाजित करने पर शेष 3 मिलते हैं, इसलिए जनवरी में 3 अजीब दिन होते हैं। सामान्यीकरण करते हुए, कोई भी महीना जिसमें 31 दिन होते हैं, उसमें 3 अजीब दिन होते हैं और किसी महीने में 30 दिन होने पर 2 अजीब दिन होते हैं। एकमात्र अपवाद फरवरी का है।
• साधारण वर्ष में फरवरी में 28 दिन होते हैं, संख्या 28 को 7 से विभाजित करने पर शेष 0 मिलता है। इसलिए, साधारण वर्ष में फरवरी में 0 अजीब दिन होते हैं और लीप वर्ष में 1 अजीब दिन होता है क्योंकि लीप वर्ष में फरवरी में 29 दिन होते हैं। नीचे दी गई तालिका कैलेंडर वर्ष के विभिन्न महीनों में अजीब दिनों की संख्या को दर्शाती है:

• साधारण वर्ष में 365 दिन होते हैं, जिसका अर्थ है 52 x 7 + 1, यानी 52 सप्ताह और एक दिन। इस अतिरिक्त दिन को अजीब दिन कहा जाता है। अजीब दिनों की अवधारणा कैलेंडर में बहुत महत्वपूर्ण है।
• एक सदी - यानी 100 वर्ष में 24 लीप वर्ष और 76 गैर-लीप वर्ष होते हैं। इसका अर्थ है कि 24 x 2 + 76 x 1 = 124 अजीब दिन होंगे। चूंकि 7 अजीब दिन एक सप्ताह बनाते हैं, इसलिए कुल अजीब दिनों की संख्या ज्ञात करने के लिए 124 को 7 से विभाजित करें। शेष 5 है। यह सदी में अजीब दिनों की संख्या है।
• आप परीक्षा के दौरान समय बचाने के लिए कैलेंडर की अवधारणाओं से संबंधित निम्नलिखित बिंदुओं को याद कर सकते हैं: (i) 100 वर्ष में हमें 5 अजीब दिन मिलते हैं जैसा कि ऊपर गणना की गई है। (ii) 200 वर्ष में 5 x 2 = 10-7 (एक सप्ताह) => 3 अजीब दिन मिलते हैं। (iii) 300 वर्ष में 5 x 3 = 15-14 (दो सप्ताह) => 1 अजीब दिन मिलता है। (iv) 400 वर्ष में {5 x 4 + 1 (लीप सदी)} - 21 => 0 अजीब दिन मिलते हैं।
• अब, यदि हम 1 जनवरी 0001 ईस्वी से शुरू करें; 0 अजीब दिनों के लिए, दिन रविवार होगा; 1 अजीब दिन के लिए, दिन सोमवार होगा; 2 अजीब दिनों के लिए, दिन मंगलवार होगा; 3 अजीब दिनों के लिए, दिन बुधवार होगा और इसी तरह।

2. अजीब दिनों की गणना

• 1 सामान्य वर्ष = 365 दिन = (52 सप्ताह 1 दिन)। 1 सामान्य वर्ष में 1 विषम दिन होता है।
• 1 लीप वर्ष = 366 दिन = (52 सप्ताह 2 दिन) 1 लीप वर्ष में 2 विषम दिन होते हैं।
• 100 वर्ष = 76 सामान्य वर्ष + 24 लीप वर्ष = (76 x 1 + 24 x 2) विषम दिन = 124 विषम दिन = (17 सप्ताह 5 दिन)।
• 400 वर्षों में विषम दिनों की संख्या = (5 x 4 + 1) 0 विषम दिन।

लीप वर्ष का अवधारणा

• प्रत्येक 100वां वर्ष, 1 ए.डी. से शुरू होकर, एक गैर-लीप वर्ष होता है, लेकिन प्रत्येक 4वीं सदी का वर्ष एक लीप वर्ष होता है।
• कोई भी वर्ष जो 400 से पूरी तरह विभाजित होता है, वह एक लीप वर्ष होगा, जैसे: 1200, 1600 और 2000।
• और वर्ष 1800, 1900 गैर-लीप वर्ष होंगे क्योंकि ये 100 से विभाजित होते हैं, लेकिन 400 से नहीं।

लीप वर्ष का मूल्यांकन

लीप वर्ष हर चार वर्षों में होता है, लेकिन कुछ परिस्थितियों में, दो लीप वर्षों के बीच का अंतर 4 वर्षों के बजाय 8 वर्ष होता है। उदाहरण: वर्ष 1896 एक लीप वर्ष है। अगला लीप वर्ष 1904 में आता है (1900 लीप वर्ष नहीं है)। किसी भी वर्ष को जो 4 से पूरी तरह विभाजित होता है (शेष शून्य होता है) उसे लीप वर्ष माना जाता है। उदाहरण: 1888, 2012, 2016 लीप वर्ष हैं क्योंकि ये 4 से पूरी तरह विभाजित होते हैं। वर्ष जैसे 2009, 2019 आदि पूरी तरह 4 से विभाजित नहीं होते, इसलिए ये सामान्य वर्ष हैं। एक अपवाद: वर्ष 700 पूरी तरह 4 से विभाजित होता है, लेकिन इसे लीप वर्ष नहीं माना जाता। एक सदी के वर्ष के लिए, यह तर्क करता है कि यह हमेशा 400 से विभाजित होना चाहिए, न कि 4 से। हालांकि वर्ष 700 4 से विभाजित है लेकिन 400 से नहीं। इसलिए, वर्ष 700 को लीप वर्ष नहीं माना जा सकता। उदाहरण: 400, 800, 1200 आदि लीप वर्ष हैं क्योंकि ये 400 से विभाजित होते हैं और वर्ष 300, 700, 100 आदि लीप वर्ष नहीं हैं क्योंकि ये 400 से विभाजित नहीं होते।

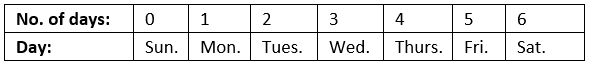
साधारण वर्ष क्या है?

पंचांग गणनाएँ

किसी भी दिए गए वर्ष की तारीख का दिन जानने के लिए, आपको पंचांग गणनाओं को समझना होगा:

• 1 जनवरी 1 ईस्वी सोमवार था, इसलिए हमें रविवार से दिन गिनना होगा। इसका मतलब है कि 0वां दिन रविवार था, इसलिए 7वां दिन भी रविवार होगा, और इसी तरह आगे। हर सातवें दिन दिन दोहराया जाता है (सप्ताह का सिद्धांत)। यदि आज सोमवार है, तो 28वां दिन भी सोमवार होगा क्योंकि यह 7 का गुणनखंड है (28/7 = 4, यानी चार सप्ताह)। यहां 30 दिन की गणना 30/7 से की जाएगी, जो 4 सप्ताह और 2 दिन है, इन दो दिनों को असामान्य दिन कहा जाता है। सोमवार से शुरू करते हुए और दो असामान्य दिनों के साथ, दिन बुधवार होगा; यह बिंदु कैलेंडर में सबसे महत्वपूर्ण है।
• दूसरे दृष्टिकोण से देखने पर, चूंकि 28वां दिन सोमवार है, इसलिए 30वां दिन बुधवार होगा। लेकिन आपको असामान्य दिनों के सिद्धांत को समझना और उपयोग करना होगा क्योंकि प्रश्न हजारों वर्षों के बारे में हो सकता है।
• एक साधारण वर्ष में 365 दिन होते हैं, इसलिए 52 सप्ताह और 1 असामान्य दिन होता है; एक लीप वर्ष में 366 दिन होते हैं, इसलिए 52 सप्ताह और 2 असामान्य दिन होते हैं।
• 100 वर्षों में 24 लीप वर्ष और 76 साधारण वर्ष होते हैं, इसलिए असामान्य दिनों की संख्या 24(2) + 76 = 124 है, जो 17 सप्ताह और 5 असामान्य दिन हैं, इसलिए 100 वर्षों में 5 असामान्य दिन होते हैं।
• 200 वर्षों में असामान्य दिनों की संख्या 100 वर्षों की संख्या का दो गुना होती है, जो 10 है, जो एक सप्ताह और 3 असामान्य दिन हैं, इसलिए 200 वर्षों में 3 असामान्य दिन होते हैं।
• 300 वर्षों में, असामान्य दिनों की संख्या 15 होती है, जो दो सप्ताह और 1 असामान्य दिन है, इसलिए 300 वर्षों में 1 असामान्य दिन होता है।
• 400 वर्ष एक लीप वर्ष होता है; इसी प्रकार, 400 के गुणनखंड भी लीप वर्ष होते हैं।
• 400 वर्षों में असामान्य दिनों की संख्या 20 + 1 (लीप वर्ष से) होती है, इसलिए कुल दिनों की संख्या 21 होती है, जो तीन सप्ताह और 0 असामान्य दिन हैं। 400 वर्षों में 0 असामान्य दिन होते हैं।

प्रकार 1 समस्याएँ: जब एक दिन दिया जाता है तो उस दिन को खोजने की समस्या।

प्रश्न 2: यदि आज रविवार है, तो 7777वें दिन कौन सा दिन होगा? हल: यदि आज रविवार है, तो आज से 7वां दिन रविवार होगा। इसी तरह, 14वां दिन, 21वां दिन, 70वां दिन, 700वां दिन, 7000वां दिन या 7777वां दिन भी रविवार होगा। इसलिए, उत्तर रविवार है।

टाइप 2 समस्याएँ: जब कोई अन्य दिन नहीं दिया गया हो, तब दिन ज्ञात करें।

इस अनुभाग में, एक दिए गए दिनांक का सप्ताह का दिन निर्धारित करना है। यहाँ कोई संदर्भ दिनांक या दिन नहीं दिया गया है। उत्तर ज्ञात करने के लिए अजीब दिन की अवधारणा का उपयोग किया जा सकता है।

प्रश्न 1: 15 अगस्त 1947 को सप्ताह का कौन सा दिन था? हल: 15 अगस्त 1947 की दिनांक को सरल गणना के लिए निम्नलिखित रूप से विभाजित किया जा सकता है:

• 1600 वर्ष
• 300 वर्ष
• 46 वर्ष (1901 से 1946)
• 1 जनवरी से 15 अगस्त (1947 तक)

नोट: तीसरे खंड में 47 वर्ष नहीं लिखें, इससे यह संकेत मिलेगा कि उस सदी का 47वां वर्ष समाप्त हो गया है।

अब हम प्रत्येक खंड में अजीब दिनों की कुल संख्या ज्ञात करते हैं:

खंड 1: 1600 400 वर्षों का गुणज है। 400 वर्षों में 0 अजीब दिन होते हैं, इसलिए 1600 वर्षों में 0 अजीब दिन होने चाहिए।

खंड 2: दूसरे खंड में 30 वर्षों में 1 अजीब दिन होगा। स्पष्टीकरण के लिए "एक सदी में अजीब दिनों का मूल्यांकन" विषय को संदर्भित करें।

खंड 3: इस खंड में 1901 से 1946 तक 46 वर्ष हैं। हम जानते हैं कि एक सामान्य वर्ष में 1 अजीब दिन और एक लीप वर्ष में 2 अजीब दिन होते हैं।

अब हम 1901 से 1946 तक के कुल लीप वर्षों की संख्या ज्ञात करते हैं। 46 को 4 से विभाजित करने पर भागफल 11 आता है, जो इंगित करता है कि 1901 से 1946 तक 11 लीप वर्ष हैं। यदि 46 वर्षों में 11 लीप वर्ष हैं, तो शेष 35 वर्ष सामान्य वर्ष होने चाहिए। इसलिए, 35 सामान्य वर्षों में 35 अजीब दिन होंगे और 11 लीप वर्षों में 11*2 = 22 अजीब दिन होंगे। 46 वर्षों में अजीब दिनों की कुल संख्या 35 + 22 = 57 अजीब दिन होगी। 57 को 7 से विभाजित करने पर शेष 1 आता है। इससे यह संकेत मिलता है कि 1901 से 1946 के बीच केवल एक अजीब दिन है।

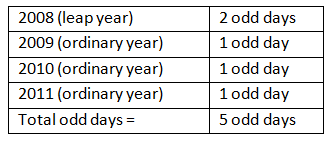
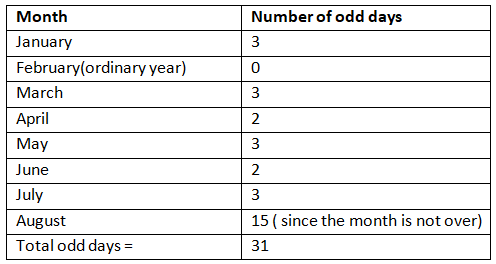
अनुभाग 4: इसमें जनवरी से 15 अगस्त तक के महीने शामिल हैं। हमने पहले ही प्रत्येक महीने में विषम दिनों की कुल संख्या की गणना विषम दिनों के खंड में की है। चूंकि 1947 एक लीप वर्ष नहीं था, फरवरी में शून्य विषम दिन थे। महीने में विषम दिनों की संख्या को बेहतर समझने के लिए नीचे दिए गए तालिका को देखें: विषम दिनों की कुल संख्या 31 है, जिसे 7 से विभाजित करने पर शेष 3 मिलता है। इसलिए, वर्ष 1947 में 1 जनवरी से 15 अगस्त तक विषम दिनों की कुल संख्या 3 है। प्रत्येक खंड के विषम दिनों की कुल संख्या जोड़ने पर: विषम दिनों की कुल संख्या = 0 + 1 + 1 + 3 = 5 = शुक्रवार। इसलिए, 15 अगस्त 1947 को शुक्रवार था।

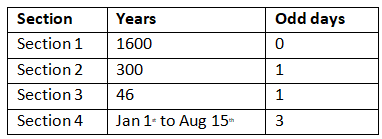
प्रकार 3 समस्याएँ: कैलेंडर मिलाना

प्रश्न: भविष्य में कौन सा वर्ष 2009 के समान कैलेंडर होगा? (क) 2010 (ख) 2013 (ग) 2015 (घ) 2017 उत्तर: (ग) इसलिए: यदि किसी भी वर्षों के बीच विषम दिनों की कुल संख्या शून्य है या यह सात का गुणनखंड है। तो, उन दोनों वर्षों का कैलेंडर समान होगा। विषम दिनों की कुल संख्या नीचे सूचीबद्ध है: इसलिए, 2015 का कैलेंडर 2009 के समान होगा। विकल्प (ग) सही उत्तर है।

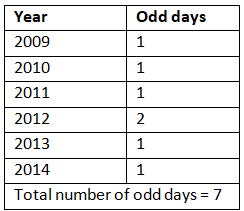
समाधान किए गए उदाहरण

उदाहरण 1: 9 फरवरी 1979 को कौन सा दिन था?

• आप जानते हैं कि 1600 वर्षों में 0 अजीब दिन होंगे। और अगले 300 वर्षों में 1 अजीब दिन होगा।
• 1901 से 1978 तक हमारे पास 19 लीप वर्ष और 59 गैर-लीप वर्ष हैं। इसलिए, 31 दिसंबर 1978 तक कुल अजीब दिनों की संख्या है 19 x 2 + 59 = 97।
• 97 को 7 से विभाजित करने पर हमें 6 शेष मिलता है, जो इन वर्षों में कुल अजीब दिनों की संख्या है।
• इसलिए, 31 दिसंबर 1978 तक, हमारे पास 1 + 6 = 7 अजीब दिन हैं, जो एक पूर्ण सप्ताह बनाते हैं।
• अब, 1979 में, जनवरी में 3 अजीब दिन हैं, और फरवरी के महीने में (9 फरवरी तक) 2 अजीब दिन हैं। इसलिए, कुल अजीब दिन हैं 3 + 2 = 5।

इसलिए, 9 फरवरी 1979 को शुक्रवार था।

उदाहरण 2: यदि 10 मई 1997 को सोमवार था, तो 10 अक्टूबर 2001 को क्या दिन होगा?

• इस प्रश्न में संदर्भ बिंदु 10 मई 1997 है, और आपको 10 मई 1997 से 10 अक्टूबर 2001 तक अजीब दिनों की संख्या निकालनी है।
• अब, 11 मई 1997 - 10 मई 1998 = 1 अजीब दिन
• 11 मई 1998 - 10 मई 1999 = 1 अजीब दिन
• 11 मई 1999 - 10 मई 2000 = 2 अजीब दिन (2000 लीप वर्ष था)
• 11 मई 2000 - 10 मई 2001 = 1 अजीब दिन
• इस प्रकार, 10 मई 2001 तक कुल अजीब दिनों की संख्या = 5।
• अब, मई के शेष 21 दिन 0 अजीब दिन देंगे। जून में, हमारे पास 2 अजीब दिन हैं; जुलाई में, 3 अजीब दिन; अगस्त में, 3 अजीब दिन; सितंबर में, 2 अजीब दिन और 10 अक्टूबर तक, हमारे पास 3 अजीब दिन हैं।

इसलिए, कुल अजीब दिनों की संख्या = 18 यानी 4 अजीब दिन। चूंकि 10 मई 1997 को सोमवार था, तो सोमवार के 4 दिन बाद शुक्रवार होगा। इसलिए, 10 अक्टूबर 2001, शुक्रवार होगा।

उदाहरण 3: यदि 11 अप्रैल 1911 को मंगलवार था, तो 17 सितंबर 1915 को कौन सा दिन होगा?

• पहले सालों की दृष्टि से, वर्ष 1911 से 1912 हमें 2 विषम दिन देगा और 1913, 1914, 1915 क्रमशः 1, 1 और 1 विषम दिन देंगे।
• अब महीनों पर ध्यान केंद्रित करें। यदि आप एक महीने आगे बढ़ते हैं, अर्थात् 11 अप्रैल से 11 मई तक, तो बीच में समाप्त होने वाला महीना अप्रैल है, जो आपको 2 दिन देता है।
• इसके बाद, मई, जून, जुलाई, और अगस्त क्रमशः 3, 2, 3, और 3 विषम दिन देते हैं।
• इससे आप 11 सितंबर 1915 पर पहुँचते हैं। इसके बाद, 11 से 17 सितंबर तक के 6 और सितंबर के दिन हैं।
• विषम दिनों की कुल संख्या है 2 + 1 + 1 + 1 + 2 + 3 + 2 + 3 + 3 + 6 = 24।
• इसमें से 21 (3 पूर्ण सप्ताह) घटाने पर बचे हुए विषम दिनों की संख्या 3 है। दिए गए दिन, अर्थात् मंगलवार में तीन दिन जोड़ने पर उत्तर शुक्रवार बनता है।

उदाहरण 4: यदि 15 मार्च 1816 शुक्रवार था, तो 15 अप्रैल 1916 कौन सा दिन होगा?

• हमें दिया गया है कि 15 मार्च 1816 एक शुक्रवार था। अब हम जानते हैं कि 100 वर्षों में 5 विषम दिन होते हैं। इसलिए 15 मार्च 1916 तक, हमारे पास 5 विषम दिन होंगे।
• तो 15 मार्च 1816 से 15 मार्च 1916 तक पहुंचने पर हमें 5 विषम दिन मिलेंगे।
• अब 15 मार्च 1916 से 15 अप्रैल 1916 तक 3 विषम दिन होंगे।
• इसलिए विषम दिनों की कुल संख्या = 5 + 3 = 8, 8 को 7 से भाग देने पर शेष 1। तो, 15 अप्रैल 1916 शुक्रवार 1 = शनिवार होगा।

उदाहरण 5:Leap वर्ष 1895 का कैलेंडर वर्ष X के समान है। निम्नलिखित में से X का कौन सा मान संभावित है?

1895 एक लीप वर्ष नहीं है। इसलिए, इसमें 1 विषम दिन होगा। चूंकि, 1896 एक लीप वर्ष है, यह 2 विषम दिन जोड़ेगा। इसी प्रकार, 1987, 1898, 1899, 1900 में 1, 1, 1, 1 विषम दिन जोड़े जाएंगे। अब कुल विषम दिनों की संख्या 7 है। इसलिए, अगला वर्ष 1901 का कैलेंडर 1895 के समान होगा।

• 1895 एक लीप वर्ष नहीं है।

महत्वपूर्ण सूत्र: CAT कैलेंडर

• विषम दिन: यदि प्रश्न में किसी विशेष तिथि पर सप्ताह का दिन ज्ञात करने के लिए पूछा गया है, तो छात्रों को विषम दिनों के सिद्धांत का उपयोग करना होगा। पूर्ण सप्ताह से अधिक दिनों की संख्या को विषम दिन कहा जाता है।
• लीप वर्ष: हर वर्ष जो 4 से विभाज्य है, एक लीप वर्ष है और हर चौथा सदी एक लीप वर्ष है और कोई अन्य सदी लीप वर्ष नहीं है। उदाहरण के लिए, 1948, 2004, 1676 - इनमें से प्रत्येक एक लीप वर्ष है। 400, 800, 1200, 1600, 2000 - इनमें से प्रत्येक एक लीप वर्ष है। 2001, 2002, 2003, 2005, 1800, 2100 - इनमें से कोई भी लीप वर्ष नहीं है।
• साधारण वर्ष: जो वर्ष लीप वर्ष नहीं है, उसे साधारण वर्ष कहा जाता है। एक साधारण वर्ष में कुल 365 दिन होते हैं।
• विषम दिनों की गणना: 1 वर्ष में कुल 52 सप्ताह और 1 दिन होता है। इसलिए, 1 साधारण वर्ष में 1 विषम दिन होता है। 1 लीप वर्ष में 52 सप्ताह और 2 दिन होते हैं। इसलिए, 1 लीप वर्ष में 2 विषम दिन होते हैं। 100 वर्षों में 76 साधारण वर्ष और 24 लीप वर्ष होते हैं = (76 x 1 + 24 x 2) विषम दिन = 124 विषम दिन। = (17 सप्ताह + 5 विषम दिन)। इसलिए, 100 वर्षों में विषम दिनों की संख्या 5 है।
• 200 वर्षों में विषम दिनों की संख्या होगी (5 x 2) = 3 विषम दिन।
• 300 वर्षों में विषम दिनों की संख्या होगी (5 x 3) = 1 विषम दिन।
• 400 वर्षों में विषम दिनों की संख्या होगी (5 x 4 + 1) = 0 विषम दिन।