कैलेंडर: हल किए गए उदाहरण | General Intelligence & Reasoning for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA PDF Download

प्रश्न 1: यदि 15 मार्च 1816 शुक्रवार था, तो 15 अप्रैल 1916 कौन सा दिन होगा? A. सोमवार B. बुधवार C. गुरुवार D. शनिवार

उत्तर: D हमें दिया गया है कि 15 मार्च 1816 एक शुक्रवार था। अब हम जानते हैं कि 100 वर्षों में 5 अजीब दिन होते हैं। इसलिए 15 मार्च 1916 तक, हमारे पास 5 अजीब दिन होंगे। तो यदि हम 15 मार्च 1816 से 15 मार्च 1916 तक चलते हैं, तो हमें 5 अजीब दिन मिलेंगे। अब 15 मार्च 1916 से 15 अप्रैल 1916 तक 3 अजीब दिन होंगे। कुल अजीब दिनों की संख्या = 5 + 3 = 8; 8 का 7 में भाग देने पर शेष = 1। इसलिए 15 अप्रैल 1916 शनिवार होगा।

प्रश्न 2: लीप वर्ष 1895 का कैलेंडर वर्ष X के समान है। निम्नलिखित में से X का संभावित मान कौन सा है? A. 1900 B. 1901 C. 1902 D. 1903

उत्तर: B 1895 एक लीप वर्ष नहीं है। इसलिए इसके पास 1 अजीब दिन होगा। चूंकि 1896 एक लीप वर्ष है, यह 2 अजीब दिन जोड़ेगा। इसी तरह 1897, 1898, 1899, 1900 में 1, 1, 1, 1 अजीब दिन जुड़ेंगे। अब कुल अजीब दिनों की संख्या 7 हो जाएगी। इसलिए अगले वर्ष 1901 का कैलेंडर 1895 के समान होगा।

प्रश्न 3: यदि 28 अगस्त 1946 बुधवार था, तो 31 अगस्त 1961 कौन सा दिन था? A. मंगलवार B. गुरुवार C. सोमवार D. बुधवार

उत्तर: B दिया गया है कि 28 अगस्त 1946 बुधवार था। 28 अगस्त 1946 से 28 अगस्त 1961 तक, हमारे पास 4 लीप वर्ष और 11 सामान्य वर्ष हैं। इसलिए अजीब दिनों की संख्या होगी 11x1 + 4x2 = 19। अब जो तारीख पूछी गई है वह 31 अगस्त 1961 है। इसलिए यदि हम 28 अगस्त से 31 अगस्त तक चलते हैं, तो हमें 3 और अजीब दिन मिलेंगे। कुल अजीब दिनों की संख्या = 5 + 3 = 8; अब 8 का 7 में भाग देने पर शेष = 1। इसलिए 31 अगस्त 1961 बुधवार होगा, 1 = गुरुवार।

प्रश्न 4: यदि 09/12/2001 (DD/MM/YYYY) रविवार है, तो 09/12/1971 कौन सा दिन होगा?
A. बुधवार
B. मंगलवार
C. शनिवार
D. गुरुवार

उत्तर: D 30 साल। अधिवर्षों की संख्या 8 है (1972, 1976, 1980, 1984, 1988, 1992, 1996, 2000)। इसलिए, कुल दिनों की संख्या = 22 × 365 + 8 × 366 = 10958
10958 mod 7 = 3। चूंकि 09/12/2001 रविवार है, 09/12/1971 गुरुवार होना चाहिए।

प्रश्न 5: 2016 में, मोहन ने शुक्रवार को अपना जन्मदिन मनाया। 2016 के बाद पहला वर्ष कब होगा जब मोहन बुधवार को अपना जन्मदिन मनाएगा? (वह जनवरी या फरवरी में जन्मा नहीं है)
A. 2021
B. 2023
C. 2020
D. 2025

उत्तर: C चूंकि यह उल्लेख किया गया है कि मोहन फरवरी में जन्मा नहीं है, इसलिए वह 29 फरवरी को जन्मा नहीं हो सकता। इसलिए, वह उस वर्ष में बुधवार को अपना अगला जन्मदिन मनाएगा जब विषम दिनों का योग 5 या 5 का गुणांक हो। 2017 में उसके जन्मदिन पर 1 विषम दिन होगा। 2018 में उसके जन्मदिन पर 2 विषम दिन होंगे। 2019 में उसके जन्मदिन पर 3 विषम दिन होंगे। 2020 में उसके जन्मदिन पर 5 विषम दिन होंगे, क्योंकि 2020 एक अधिवर्ष है। इसलिए 2020 में वह बुधवार को अपना जन्मदिन मनाएगा।

प्रश्न 6: 28 मई, 2006 को किस दिन का सप्ताह है?
A. शनिवार
B. सोमवार
C. रविवार
D. गुरुवार

उत्तर: C 28 मई 2006 = (2005 वर्षों की अवधि 1-Jan-2006 से 28-May-2006 तक) हमें पता है कि 400 वर्षों में विषम दिनों की संख्या = 0 है। इसलिए 2000 वर्षों में विषम दिनों की संख्या = 0 (क्योंकि 2000, 400 का सही गुणांक है)। 2001-2005 की अवधि में विषम दिनों की संख्या = 4 सामान्य वर्ष + 1 अधिवर्ष = 4 × 1 + 1 × 2 = 6 दिन। 1-Jan-2006 से 28-May-2006 तक = 31 (जनवरी) + 28 (फरवरी) + 31 (मार्च) + 30 (अप्रैल) + 28 (मई) = 148। 148 दिन = 21 सप्ताह + 1 दिन = 1 विषम दिन। कुल विषम दिनों की संख्या = (0 + 6 + 1) = 7 विषम दिन = 0 विषम दिन। 0 विषम दिन = रविवार। इसलिए 28 मई 2006 रविवार है।

प्रश्न 7: 15 अगस्त, 2010 का सप्ताह का दिन क्या होगा? A. गुरुवार B. रविवार C. सोमवार D. शनिवार

उत्तर: B 15 अगस्त 2010 = (1 जनवरी 2010 से 15 अगस्त 2010 तक 2009 वर्षों की अवधि) हम जानते हैं कि 400 वर्षों में असामान्य दिनों की संख्या = 0 है। इसलिए 2000 वर्षों में असामान्य दिनों की संख्या = 0 है (चूंकि 2000, 400 का पूर्ण गुणांक है)। 2001-2009 की अवधि में असामान्य दिनों की संख्या = 7 सामान्य वर्ष + 2 लीप वर्ष = 7 x 1 + 2 x 2 = 11 = (11 - 7x1) असामान्य दिन = 4 असामान्य दिन। 1 जनवरी 2010 से 15 अगस्त 2010 तक के दिन = 31 (जनवरी) + 28 (फरवरी) + 31 (मार्च) + 30 (अप्रैल) + 31 (मई) + 30 (जून) + 31 (जुलाई) + 15 (अगस्त) = 227। 227 दिन = 32 सप्ताह + 3 दिन = 3 असामान्य दिन। कुल असामान्य दिनों की संख्या = (0 + 4 + 3) = 7 असामान्य दिन = 0 असामान्य दिन। 0 असामान्य दिन = रविवार। इसलिए 15 अगस्त, 2010 रविवार है।

प्रश्न 8: आज सोमवार है। 61 दिनों बाद यह क्या होगा? A. गुरुवार B. रविवार C. सोमवार D. शनिवार

उत्तर: D 61 दिन = 8 सप्ताह + 5 दिन = 5 असामान्य दिन। इसलिए यदि आज सोमवार है, तो 61 दिनों बाद यह होगा = (सोमवार + 5 असामान्य दिन) = शनिवार।

प्रश्न 9: अप्रैल 2001 के किन तारीखों को बुधवार पड़ा? A. 2, 9, 16, 23

B. 4, 11, 18, 25

C. 3, 10, 17, 24

D. 1, 8, 15, 22, 29

उत्तर: B हमें 01-अप्रैल-2001 का दिन पता करना है। 01-अप्रैल-2001 = (1 जनवरी 2001 से 01-अप्रैल-2001 तक 2000 वर्षों की अवधि) हम जानते हैं कि 400 वर्षों में असामान्य दिनों की संख्या = 0 है। इसलिए 2000 वर्षों में असामान्य दिनों की संख्या = 0 है (चूंकि 2000, 400 का पूर्ण गुणांक है)। 1 जनवरी 2001 से 01-अप्रैल-2001 तक के दिन = 31 (जनवरी) + 28 (फरवरी) + 31 (मार्च) + 1 (अप्रैल) = 91। 91 दिन = 13 सप्ताह = 0 असामान्य दिन। कुल असामान्य दिनों की संख्या = (0 + 0) = 0 असामान्य दिन। 0 असामान्य दिन = रविवार। इसलिए 01-अप्रैल-2001 रविवार है। इसलिए अप्रैल 2011 का बुधवार 04, 11, 18 और 25 को आता है।

प्रश्न 10: x सप्ताहों में कुल कितने दिन होते हैं? A. 14x B. 8x

C. 7x² D. 7

उत्तर: B

x सप्ताहों में दिन = (7 × x) x = 7x x = 8x = (7 × x) x = 7x x = 8x दिन

प्रश्न 11: वर्ष 2007 के लिए कैलेंडर वर्ष A. 2017 B. 2018 C. 2014 D. 2016 के लिए समान होगा।

2007 के कैलेंडर के समान होने के लिए, 2007 से कुल अजीब दिन 0 होने चाहिए।

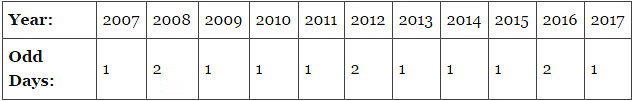
वर्ष: 2007 2008 2009 2010 2011 2012 2013 2014 2015 2016 2017

अजीब दिन: 1 2 1 1 1 2 1 1 1 2 1 योगफल = 14 अजीब दिन ≡ 0 अजीब दिन।

इसलिए, वर्ष 2018 का कैलेंडर वर्ष 2007 के समान होगा।

प्रश्न 12: निम्नलिखित में से कौन सा लीप वर्ष नहीं है? A. 1200 B. 800 C. 700 D. 2000

उत्तर: C लीप वर्ष का नियम याद रखें: (सूत्रों में दिया गया) 1. हर वर्ष जो 4 से विभाज्य है, वह लीप वर्ष है, यदि वह शताब्दी नहीं है। 2. हर चौथी शताब्दी एक लीप वर्ष है, लेकिन कोई अन्य शताब्दी लीप वर्ष नहीं है। 800, 1200 और 2000 चौथी शताब्दी की श्रेणी में आते हैं (जैसे 400, 800, 1200, 1600, 2000 आदि)। इसलिए 800, 1200 और 2000 लीप वर्ष हैं। 700 चौथी शताब्दी नहीं है, लेकिन यह एक शताब्दी है। इसलिए यह लीप वर्ष नहीं है।

प्रश्न 13: 01-जनवरी-2007 सोमवार था। 01-जनवरी-2008 को सप्ताह का कौन सा दिन होगा? A. बुधवार B. रविवार C. शुक्रवार D. मंगलवार

उत्तर: D दी गई जानकारी: 1 जनवरी 2007 को सोमवार था। 2007 में अजीब दिन = 1 (हमने पूरे वर्ष 2007 को लिया है क्योंकि हमें 01-जनवरी-2007 से 31-दिसंबर-2007 तक के अजीब दिन जानने हैं, अर्थात् पूरा वर्ष 2007)। इसलिए 1 जनवरी 2008 = (सोमवार + 1 अजीब दिन) = मंगलवार।

प्रश्न 14: 8 दिसंबर 2007 शनिवार था, 8 दिसंबर 2006 को सप्ताह का कौन सा दिन था? A. रविवार B. मंगलवार C. शुक्रवार D. मंगलवार

उत्तर: C यह देखते हुए कि 8 दिसंबर 2007 शनिवार था, 8 दिसंबर 2006 से 7 दिसंबर 2007 तक के दिनों की संख्या = 365 दिन। 365 दिन = 1 विषम दिन। इसलिए 8 दिसंबर 2006 था = (शनिवार - 1 विषम दिन) = शुक्रवार।

प्रश्न 15: 8 फरवरी, 2005 को मंगलवार था। 8 फरवरी, 2004 को सप्ताह का कौन सा दिन था? A. रविवार B. शुक्रवार C. शनिवार D. सोमवार

उत्तर: A यह देखते हुए कि 8 फरवरी, 2005 मंगलवार था, 8 फरवरी, 2004 से 7 फरवरी, 2005 तक के दिनों की संख्या = 366 (चूंकि फरवरी 2004 में 29 दिन हैं क्योंकि यह लीप वर्ष है। 366 दिन = 2 विषम दिन)। इसलिए 8 फरवरी, 2004 = (मंगलवार - 2 विषम दिन) = रविवार।