ज्यामिति प्रश्नों के उत्तर - 3 | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA PDF Download

प्रश्न 21: 6 सेमी की भुजा वाला समचतुर्भुज एक नियमित अष्टकोण के बाहरी कोण के बराबर एक कोण रखता है। समचतुर्भुज का क्षेत्रफल ज्ञात कीजिए।

A. 18√2 सेमी²

B. 9√2 सेमी²

C. 15√2 सेमी²

D. 12√2 सेमी²

उत्तर. 18√2 सेमी²

व्याख्या।

समचतुर्भुज की भुजा 's' = 6 सेमी

भुजाओं के बीच का कोण 'a' = अष्टकोण का बाहरी कोण

अतः a = 45 डिग्री

समचतुर्भुज का क्षेत्रफल = sin a * s²

क्षेत्रफल = (1/√2) * 36

क्षेत्रफल = 18√2 सेमी²

प्रश्न है "समचतुर्भुज का क्षेत्रफल ज्ञात कीजिए।"

अतः, उत्तर है 18√2 सेमी².

विकल्प A सही उत्तर है।

प्रश्न 22: 2 की भुजा वाले वर्ग में एक वृत्त inscrit है, जिसमें एक समभुज त्रिकोण inscrit है। समभुज त्रिकोण का क्षेत्रफल और वर्ग का क्षेत्रफल का अनुपात क्या है?

A. 9√3 : 16

B. 3√3 : 4

C. 9√3 : 4

D. 3√3 : 16

उत्तर. 3√3 : 16

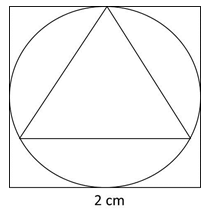
वृत्त की त्रिज्या 1 इकाई है। यदि हम समभुज त्रिकोण की भुजा को 'a' मानते हैं, तो समभुज त्रिकोण की परिसीमा है

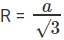
अतः, a = √3

इसलिए, समभुज त्रिकोण और वर्ग के क्षेत्रफल का अनुपात है

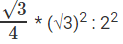
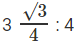
प्रश्न है "समभुज त्रिकोण और वर्ग के क्षेत्रफल का अनुपात क्या है?"

अतः, उत्तर है 3√3 : 16 इकाइयाँ

विकल्प D सही उत्तर है।

प्रश्न 23: एक तीव्र कोण वाला समकर्ण त्रिकोण जिसमें दो भुजाएँ 10 और 16 के बराबर हैं। इस त्रिकोण का क्षेत्रफल ज्ञात कीजिए।

A. √231 इकाइयाँ

B. 12√66 इकाइयाँ

C. 24 इकाइयाँ

D. 5√231 इकाइयाँ

उत्तर. 5√231 इकाइयाँ

व्याख्या।

तीसरी भुजा या तो 10 या 16 है और छोटी दो भुजाओं का वर्ग का योग तीसरी भुजा के वर्ग से बड़ा होना चाहिए। 102 102 < 162="" इसलिए,="" त्रिकोण="" की="" तीसरी="" भुजा="" 16="" है।="" सेमीपरिमिटर,="" s="(10" +="" 16="" +="" 16)/2="21" क्षेत्रफल="√(21(21−16)(21−16)(21−10))" =="" √(21="" *="" 5="" *="" 5="" *="" 11)="5√231" />

प्रश्न है "इस त्रिकोण का क्षेत्रफल ज्ञात कीजिए।"

इसलिए, उत्तर है 5√231 इकाइयाँ।

प्रश्न 24: तीन समान वृत्त एक समभुज त्रिकोण के अंदर इस प्रकार रखे गए हैं कि कोई भी वृत्त समभुज त्रिकोण की दो भुजाओं और दो अन्य वृत्तों के लिए स्पर्श बिंदु पर है। एक वृत्त के क्षेत्रफल और त्रिकोण के क्षेत्रफल का अनुपात क्या है?

A. π : (6 + 4√3)

B. 3π : (6 + 4√3)

C. 2π : (6 + 4√3)

D. π : (6 + 2√3)

उत्तर। π : (6 + 4√3)

मान लें कि प्रत्येक वृत्त की त्रिज्या 'a' है। PQ की दूरी = 2a। AB पर PM को लंबवत खींचें ∠MAP = 30°

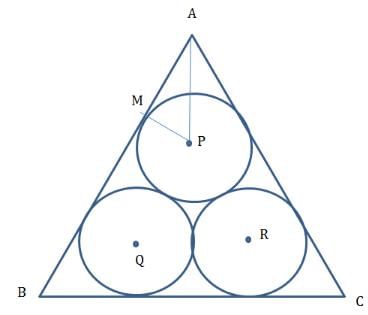
MP = a , AM = a/3 इसके बाद हम समाप्त कर चुके हैं। वृत्त का क्षेत्रफल = πa² समभुज त्रिकोण का क्षेत्रफल

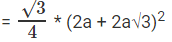
= a² (6 + 4√3) अनुपात = π : (6 + 4√3)

प्रश्न है "एक वृत्त के क्षेत्रफल और त्रिकोण के क्षेत्रफल का अनुपात क्या है?"

इसलिए, उत्तर है π : (6 + 4√3)

प्रश्न 25: एक समभुज त्रिकोण में एक वर्ग अंकित किया गया है। वर्ग की एक भुजा समभुज △ की एक भुजा पर है। वर्ग के क्षेत्रफल और समभुज त्रिकोण के क्षेत्रफल का अनुपात क्या है?

A. √3 : (5 + 4√3)

B. 2√3 : (7 + 4√3)

C. 4√3 : (7 + 4√3)

D. 4√3 : (5 + 2√3)

उत्तर। 4√3 : (7 + 4√3)

वर्ग का एक पक्ष 'a' मान लें। MN = LP = a, ∠ABC = 60°

ML = a। BL (इसके लिए कुछ त्रिकोणमिति का उपयोग करें)

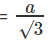
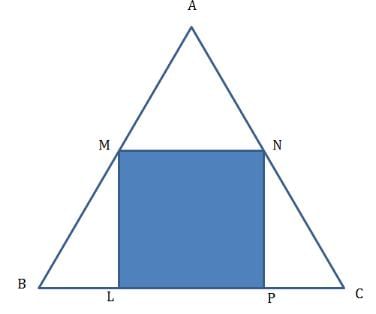
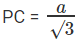
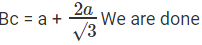
वर्ग का क्षेत्रफल = a² समकोण त्रिकोण का क्षेत्रफल

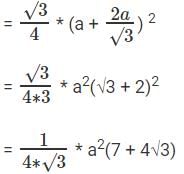
अनुपात = 4√3 : (7 4√3)

प्रश्न है "वर्ग के क्षेत्रफल का समकोण त्रिकोण के क्षेत्रफल के साथ अनुपात क्या है?"

इसलिए, उत्तर है 4√3 : (7 4√3)

चुनाव C सही उत्तर है।

प्रश्न 26: मान लें कि वर्ग S वृत्त C के भीतर है, तो S और Q के क्षेत्रफल का अनुपात क्या है? और, मान लें कि वृत्त C वर्ग S के भीतर है, तो S और Q के क्षेत्रफल का अनुपात क्या है?

A. 2:π, 4:π

B. 4:π, 2:π

C. 1:π, 4:π

D. 2:π, 1:π

उत्तर. 2:π, 4:π

यदि वर्ग वृत्त के भीतर है, तो वर्ग के क्षेत्रफल का वृत्त के क्षेत्रफल के साथ अनुपात 2 : π है।

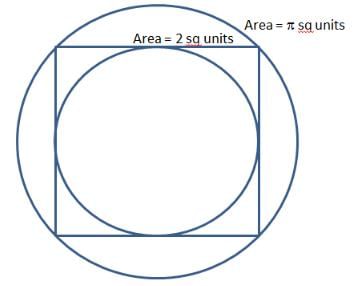
यदि वृत्त वर्ग के भीतर है, तो वर्ग के क्षेत्रफल का वृत्त के क्षेत्रफल के साथ अनुपात 4 : π है। याद रखें, वृत्त का क्षेत्रफल π के साथ और वर्ग का क्षेत्रफल संख्या के साथ है।

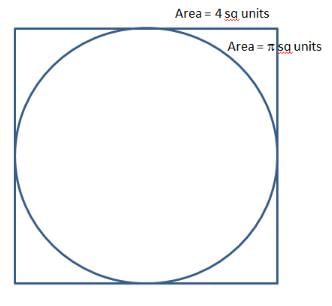
यदि वर्ग वृत्त के भीतर है, तो वर्ग के क्षेत्रफल का वृत्त के क्षेत्रफल के साथ अनुपात 2 : π है। यदि वृत्त वर्ग के भीतर है, तो वर्ग के क्षेत्रफल का वृत्त के क्षेत्रफल के साथ अनुपात 4 : π है।

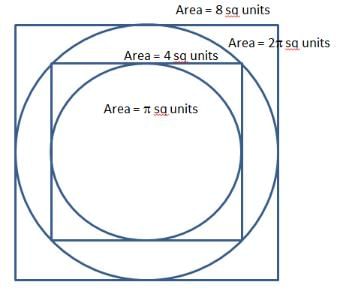
प्रश्न है "S और Q के क्षेत्रफल का अनुपात क्या है? और S और Q के क्षेत्रफल का अनुपात क्या है?"

इसलिए, उत्तर है 2:π, 4:π।

प्रश्न 27: मान लें कि समकोण त्रिकोण T वृत्त C के भीतर है, तो T और C के क्षेत्रफल का अनुपात क्या है? मान लें कि वृत्त C समकोण त्रिकोण T के भीतर है, तो T और C के क्षेत्रफल का अनुपात क्या है?

A. 3√3:π , 3√3:16π

B. 3√3:4π , 3√3:π

C. √3:π , 3√3:4π

D. √3:π , √3:16π

उत्तर: 3√3:4π , 3√3:π

किसी भी समभुज त्रिकोण की भुजा ‘a’ के लिए

इनरेडियस = और सर्कमरेडियस =

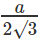
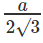
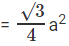
छोटी वृत्त का क्षेत्रफल

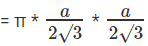
बड़ी वृत्त का क्षेत्रफल

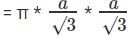
जब समभुज त्रिकोण T वृत्त C में अंकित होता है, तब T और C के क्षेत्रफल का अनुपात :: 3√3:4π जब वृत्त C समभुज त्रिकोण T में अंकित होता है, तब T और C के क्षेत्रफल का अनुपात :: 3√3:π

प्रश्न है "समभुज त्रिकोण T को वृत्त C में अंकित करें, T और C के क्षेत्रफल का अनुपात क्या है? वृत्त C को समभुज त्रिकोण T में अंकित करें, T और C के क्षेत्रफल का अनुपात क्या है?"

अत: उत्तर है 3√3:4π , 3√3:π

विकल्प B सही उत्तर है।

प्रश्न 28: नियमित षट्भुज H को वृत्त C में अंकित करें, H और C के क्षेत्रफल का अनुपात क्या है? नियमित षट्भुज H में वृत्त C को अंकित करें, H और C के क्षेत्रफल का अनुपात क्या है?

A. 2√3 : 3π , 3√3 : 4π

B. 3√3 : π , 3√3 : 4π

C. 3√3 : 2π, 2√3 : π

D. √3 : π , √3 : 4π

उत्तर: 3√3 : 2π, 2√3 : π

इनरेडियस = समभुज त्रिकोण की ऊँचाई जो कि भुजा a है = √3a/2

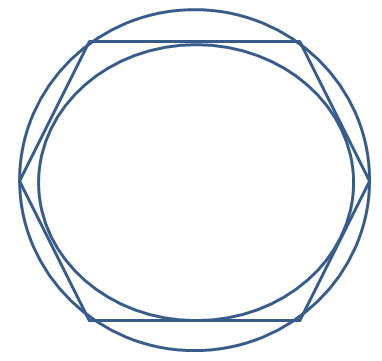
सर्कमरेडियस = a। नियमित षट्भुज का क्षेत्रफल = 6 * √3a²/4 छोटी वृत्त का क्षेत्रफल = π ∗ √3a/2 ∗ √3a/2 = 3πa²/4 बड़ी वृत्त का क्षेत्रफल = πa² जब षट्भुज H वृत्त C में अंकित होता है, तब H और C के क्षेत्रफल का अनुपात :: 3√3 : 2π जब वृत्त C नियमित षट्भुज H में अंकित होता है, तब H और C के क्षेत्रफल का अनुपात :: 2√3 : π

प्रश्न है "नियमित षट्भुज H को वृत्त C में अंकित करें, H और C के क्षेत्रफल का अनुपात क्या है? नियमित षट्भुज H में वृत्त C को अंकित करें, H और C के क्षेत्रफल का अनुपात क्या है?"

इसलिए, उत्तर है 3√3 : 2π, 2√3 : π।

प्रश्न 29: एक त्रिकोण के ऑर्थोसेन्टर और सर्कमसेन्टर के बीच की दूरी क्या है, जिसके भुजाएँ 24 सेमी, 26 सेमी और 10 सेमी हैं?

A. 13 सेमी

B. 12 सेमी

C. 7.5 सेमी

D. √30 सेमी

उत्तर: 13 सेमी

भुजाएँ 24 सेमी, 26 सेमी और 10 सेमी हैं। 10, 24, 26 एक पाइथागोरियन तिकड़ी है! इसलिए, यह एक समकोण त्रिकोण है जिसके बारे में हम बात कर रहे हैं। सर्कमसेन्टर प्राप्त करने के लिए लंबवत बिसेक्टर खींचें। ऑर्थोसेन्टर वह बिंदु है जहाँ सभी ऊँचाइयाँ मिलती हैं। एक समकोण त्रिकोण में, यह वह शिखर है जो 90 डिग्री का कोण बनाता है।

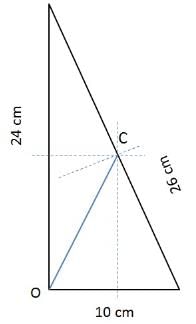
अब OC खोजना आसान है! यह बने हुए आयत के विकर्ण की लंबाई है। लंबाई = 12 सेमी, चौड़ाई = 5 सेमी विकर्ण = √(12² + 5²) = 13

प्रश्न है "एक त्रिकोण के ऑर्थोसेन्टर और सर्कमसेन्टर के बीच की दूरी क्या है, जिसके भुजाएँ 24 सेमी, 26 सेमी और 10 सेमी हैं?"

इसलिए, उत्तर है 13 सेमी।

प्रश्न 30: दो वृत्त जिनके केंद्र O1 और O2 हैं, एक बिंदु R पर बाहरी रूप से एक-दूसरे को छूते हैं। AB उस बिंदु R पर दोनों वृत्तों के लिए एक स्पर्श रेखा है। P’Q’ एक और स्पर्श रेखा है, जो उन्हें P और Q पर छू रही है और AB को S पर काट रही है। PQ की लंबाई 6 सेमी है और बिंदु S वृत्तों के केंद्रों से 5 सेमी और 4 सेमी की दूरी पर है। त्रिकोण SO1O2 का क्षेत्रफल क्या है?

A. 9 सेमी²

B. 3(4 √7)/2 सेमी²

C. 27/2 सेमी²

D. (3√41)/2 सेमी²

उत्तर: 3(4 √7)/2 सेमी²

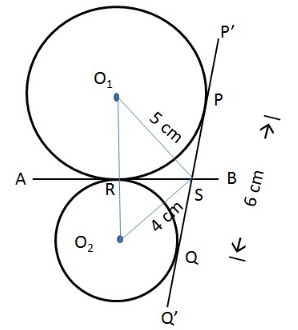
चित्र से हम देखते हैं कि SP, SR एक ही बिंदु S से वृत्त 1 के लिए स्पर्श रेखाएँ हैं। इसी प्रकार, SR, SQ एक ही बिंदु से वृत्त 2 के लिए स्पर्श रेखाएँ हैं। SP = SR; SQ = SR, इसका अर्थ है SP = SQ। PQ = 6 सेमी है, SP * SQ = 6। इसलिए SR = SP = SQ = 3 सेमी। SR त्रिकोण SO1O2 के लिए उचाई है। हमें क्षेत्रफल ज्ञात करने के लिए आधार O1O2 की लंबाई ज्ञात करनी होगी। O1RS एक समकोण त्रिकोण है जिसमें कर्ण = 5 और एक भुजा = 3। इसलिए, O1R = √(5² - 3²) = 4 सेमी। इसी प्रकार, O2RS एक समकोण त्रिकोण है जिसमें कर्ण = 4 और एक भुजा = 3। इसलिए, O2R = √(4² - 3²) = √7 सेमी। O1O2 = O1R + O2R = 4 + √7। त्रिकोण SO1O2 का क्षेत्रफल = 1/2 * SR * O1O2 = 1/2 * 3 * (4 + √7) सेमी²।

प्रश्न है "त्रिकोण SO1O2 का क्षेत्रफल क्या है?"

इसलिए, उत्तर है 3(4 √7)/2 cm².