Open App

RRB NTPC/ASM/CA/TA Exam > RRB NTPC/ASM/CA/TA Notes > Mathematics for RRB NTPC (Hindi) > ज्यामिति: हल किए गए उदाहरण - 1

ज्यामिति: हल किए गए उदाहरण - 1 | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA PDF Download

प्रश्न 1: O ΔABC के अंतर्गत एक बिंदु है, जिसमें OA = 12 सेमी, OC = 9 सेमी, ∠AOB = ∠BOC = ∠COA और ∠ABC = 60° है। OB की लंबाई (सेमी में) क्या होगी? (a) 6√2 (b) 4√6 (c) 6√3 (d) 4√3 उत्तर: (c) दी गई जानकारी:

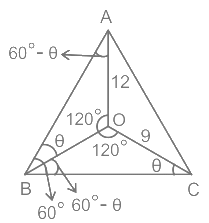
O ΔABC के अंतर्गत एक बिंदु है
OA = 12 सेमी
OC = 9 सेमी
∠AOB = ∠BOC = ∠COA
∠ABC = 60°

विचार: एक बिंदु के चारों ओर का कोण हमेशा 360° होता है। एक त्रिकोण के सभी कोणों का योग 180° होता है। गणना:

प्रश्न के अनुसार, हमें पता है कि एक बिंदु के चारों ओर का कोण हमेशा 360° होता है। तो, ⇒ ∠AOB = ∠BOC = ∠COA = 360/3 ⇒ 120° अब, ∠ABC = 60° हमें पता है कि त्रिकोण के सभी कोणों का योग 180° होता है। ΔAOB में, मान लेते हैं ∠OBA = θ ⇒ ∠OBA + ∠BAO + ∠AOB = 180° ⇒ θ + ∠BAO + 120° = 180° ⇒ ∠BAO = (180° – 120° – θ) ⇒ ∠BAO = 60° – θ अब, ΔBOC में, ⇒ ∠OBC = (∠ABC – ∠OBA) ∠OBC = 60° – θ ⇒ ∠OBC + ∠BOC + ∠OCB = 180° ⇒ (60° – θ + 120° + ∠OCB = 180° ⇒ ∠OCB = (180° – 120° – 60° – θ) ⇒ ∠OCB = θ तो, ∠AOB और ∠BOC ⇒ ∠A = ∠B ⇒ ∠O = ∠O ⇒ ∠B = ∠C ΔAOB ~ ΔBOC [AAA समानता] अब, ⇒ OB² = 108 ⇒ OB = 6√3 सेमी ∴ OB का आवश्यक मान 6√3 सेमी है।

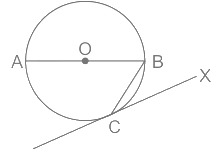
प्रश्न 2: O वृत्त का केन्द्र है। एक स्पर्श रेखा खींची गई है जो C पर वृत्त को छूती है। यदि ∠AOC = 80°, तो ∠BCX का मान (डिग्री में) क्या होगा? (a) 80 (b) 30 (c) 40 (d) 50 उत्तर: (d) दी गई जानकारी:

∠AOC = 80°

विचार: केंद्र पर तंतु द्वारा बनता कोण हमेशा उस परिधि पर किसी भी बिंदु पर बनते कोण का दो गुना होता है। गणना:

AC एक तंतु है जो वृत्त को छूता है। ⇒ ∠ABC = 1/2 × ∠AOC = 1/2 × 80 = 40° त्रिकोण OBC में, ⇒ OB = OC = वृत्त का त्रिज्या ⇒ ∠OBC = ∠OCB = 40° ⇒ ∠XCO = 90° (स्पर्श रेखा त्रिज्या के प्रति लंब होती है) ⇒ ∠BCX = ∠XCO – ∠OCB = 90 – 40 = 50° ∴ ∠BCX का मान 50° है।

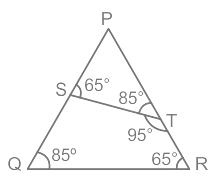
प्रश्न 3: ΔPQR में, ∠Q = 85° और ∠R = 65° हैं। बिंदु S और T PQ और PR के किनारों पर हैं, इस प्रकार कि ∠STR = 95° और QR और ST का अनुपात 9 : 5 है। यदि PQ = 21.6 सेमी है, तो PT की लंबाई क्या होगी? (a) 12 सेमी (b) 10.5 सेमी (c) 9 सेमी (d) 9.6 सेमी उत्तर: (a) दी गई जानकारी:

QR : ST = 9 : 5
PQ = 21.6 सेमी
∠Q = 85°
∠R = 65°
∠STR = 95°

विचार: यदि किसी दो कोणों का माप समान हो, तो दो त्रिकोण समान होते हैं और इसके विपरीत। गणना:

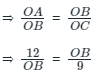
ज्यामिति: हल किए गए उदाहरण - 1 | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA

निम्नलिखित चित्र से ΔPTS ∼ PQR ⇒ QR/TS = PQ/PT ⇒ 9/5 = 21.6/PT ⇒ PT = (21.6 × 5)/9 ⇒ PT = 12 सेमी ∴ PT की लंबाई 12 सेमी है।

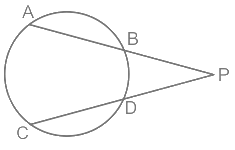
प्रश्न 4: एक वृत्त के chords AB और CD, जब बढ़ाए जाते हैं, तो वृत्त के बाहर एक बिंदु P पर मिलते हैं। यदि AB = 6 सेमी, CD = 3 सेमी और PD = 5 सेमी है, तो PB के बराबर है: (a) 6 सेमी (b) 4 सेमी (c) 5 सेमी (d) 6.25 सेमी उत्तर: (b)

दी गई जानकारी: AB = 6 सेमी, CD = 3 सेमी, PD = 5 सेमी मान लीजिए PB की लंबाई x है, PA = (x + 6) और PC = 5 + 3 = 8 सेमी। जैसा कि हम जानते हैं, PB × PA = PD × PC ⇒ x × (x + 6) = 5 × 8 ⇒ x² + 6x – 40 = 0 ⇒ x² – 10x – 40 = 0 ⇒ x (x – 10) – 4 (x + 10) = 0 ⇒ (x – 10) (x – 4) = 0 ⇒ (x – 10) = 0 ⇒ x = -10 [संभावित नहीं] ⇒ (x – 4) = 0 ⇒ x = 4

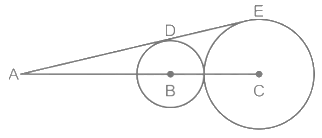
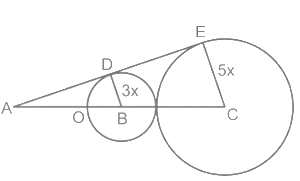
प्रश्न 5: दिए गए चित्र में, B और C दो वृत्तों के केंद्र हैं। ADE दोनों वृत्तों के लिए सामान्य स्पर्शरेखा है। यदि दोनों वृत्तों की त्रिज्या का अनुपात 3: 5 है और AC = 40 है, तो DE का मान क्या है? (a) 3√15 (b) 5√15 (c) 6√15 (d) 4√15 उत्तर: (d)

उपयोग किया गया सिद्धांत: स्पर्शरेखाएँ हमेशा त्रिज्या के साथ ⊥ होती हैं। गणना: चूंकि दोनों वृत्तों की त्रिज्या का अनुपात 3: 5 है, मान लीजिए DB = 3x और EC = 5x; चूंकि ΔABD और ΔACE समान हैं, AB : AC = 3 : 5; ∴ AB : BC = 3 : 2 ∵ AC = 40 ∴ BC = 2/5 × 40 = 16 ⇒ BC = 3x + 5x = 16 ⇒ x = 2 ∴ BD = 3x = 6 और EC = 5x = 10। ΔAEC एक समकोण त्रिकोण है; AE² = AC² – EC² AE² = 1600 – 100 = 1500 AE = 10√15 चूंकि AD : DE = 3 : 2 ∴ DE = 2/5 × 10√15 = 4√15

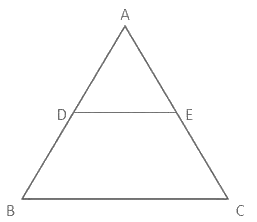
प्रश्न 6: यदि D और E त्रिभुज ABC के पक्ष AB और AC पर बिंदु हैं, ऐसा कि DE||BC। यदि AD = x सेमी, DB = (x - 3) सेमी, AE = (x + 3) सेमी और EC = (x - 2) सेमी है, तो x का मान (सेमी में) क्या है? (a) 3 (b) 3.5 (c) 4 (d) 4.5 उत्तर: (d)

दिया गया त्रिभुज नीचे दिखाया गया है। समान त्रिभुजों ∆ABC और ∆ADE पर विचार करते हुए, ⇒ AB/AD = AC/AE ⇒ (AD + DB)/AD = (AE + EC)/AE ⇒ (x + (x - 3))/x = ((x + 3) + (x - 2))/(x + 3) ⇒ (2x - 3)/x = (2x + 1)/(x + 3) ⇒ (2x - 3)(x + 3) = x(2x + 1) ⇒ 2x² + 6x - 3x - 9 = 2x² + x ⇒ 2x = 9 ∴ x = 9/2 = 4.5

प्रश्न 7: ΔABC का परिक्रमण केंद्र O है। यदि ∠BAC = 75° और ∠BCA = 80°, तो ∠OAC का मान (डिग्री में) क्या है? (a) 45 (b) 65 (c) 90 (d) 95 उत्तर: (b)

दिया गया: ΔABC में, ⇒ ∠BAC + ∠BCA + ∠ABC = 180° ⇒ ∠ABC = 180° – 75° - 80° ⇒ ∠ABC = 25° चूंकि O परिक्रमण केंद्र है ⇒ 2 × ∠ABC = ∠AOC ⇒ ∠AOC = 50° ΔAOC में, AO = OC (वृत्त की त्रिज्या) इसलिए, ΔAOC एक समद्विभाजित Δ है ⇒ ∠OAC + ∠ACO + ∠AOC = 180° ⇒ ∠OAC + ∠ACO = 180° – 50° ⇒ 2 × ∠OAC = 130° ⇒ ∠OAC = 65° ∴ सही विकल्प 2 है।

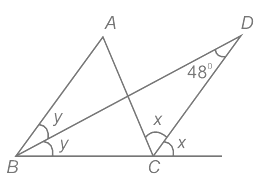
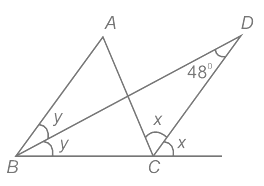
प्रश्न 8: दिए गए चित्र में, ABC एक त्रिकोण है। आंतरिक DB और बाहरी DC के विभाजक D पर मिलते हैं। यदि ∠BDC = 48°, तो ∠A का मान (डिग्री में) क्या है? (a) 48 (b) 96 (c) 100 (d) 114 उत्तर: (b)

दिया गया: आंतरिक DB और बाहरी DC के विभाजक D पर मिलते हैं। ∠BDC = 48° गणना:

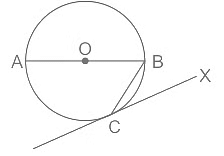
ΔBDC में बाहरी कोण गुणांक का उपयोग करते हुए ⇒ y 48 = x ⇒ x - y = 48° ......(i) ΔABC से, ⇒ ∠ACB = 180 – 2y – ∠A ......(ii) ΔBCD से, ⇒ ∠ACB = 180 – y – x – 48 ......(iii) (ii) और (iii) की तुलना करते हुए ⇒ 180 – 2y – ∠A = 180 – y – x – 48 ⇒ ∠A = x – y 48 का उपयोग करते हुए ⇒ ∠A = 48 48 = 96° ∴ ∠A का मान (डिग्री में) 96° है।

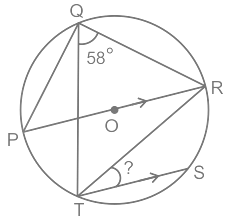
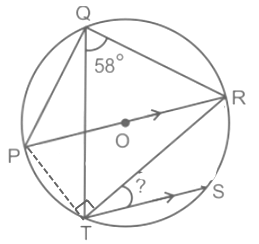
प्रश्न 9: बिंदु P, Q, R, S और T इस क्रम में एक वृत्त पर हैं जिसका केंद्र O है। यदि chord TS व्यास PR के समानांतर है और ∠RQT= 58°, तो ∠RTS का माप (डिग्री में) ज्ञात करें। (a) 45 (b) 29 (c) 32 (d) 58

उत्तर: (c) दिया गया: बिंदु P, Q, R, S और T इस क्रम में एक वृत्त पर हैं। chord TS व्यास PR के समानांतर है। ∠RQT = 58°

गणना: PR एक व्यास है। ∠PTR = 90° .....(आधा वृत्त में अंकित कोण)
∠TPR = 58° .....(समान chord पर निर्मित कोण)
इसलिए, ∠PRT = 180° - ∠PTR – ∠TPR ⇒ ∠PRT = 180° - 90° - 58° ⇒ ∠PRT = 32°
∠PRT = ∠RTS = 32° (वैकल्पिक आंतरिक कोण क्योंकि chord TS व्यास PR के समानांतर है)

∴ ∠RTS का माप 32 है।

प्रश्न 10: दिए गए चित्र में, ΔPQR में एक वृत्त अंकित है जो इसके पक्ष PQ, QR और RP को क्रमशः बिंदुओं S, T और U पर छूता है। यदि PQ = 15 सेमी, QR = 10 सेमी, और RP = 12 सेमी है, तो PS, QT और RU की लंबाई ज्ञात करें। (a) PS = 6.5 सेमी, QT = 8.5 सेमी और RU = 3.5 सेमी (b) PS = 3.5 सेमी, QT = 6.5 सेमी और RU = 8.5 सेमी (c) PS = 8.5 सेमी, QT = 6.5 सेमी और RU = 3.5 सेमी (d) PS = 8.5 सेमी, QT = 3.5 सेमी और RU = 6.5 सेमी

उत्तर: (c) मान लीजिए PS = x सेमी, तो QS = (15 – x) सेमी। PS = PU, QS = QT, RT = RU [टैंगेंट्स] ⇒ QT = (15 – x) सेमी ⇒ RT = 10 – (15 – x) = x – 5 ⇒ RU = (x – 5) ⇒ PU = 12 – x 5 = 17 – x ⇒ 17 – x = x ⇒ 2x = 17 ⇒ x = 17/2 ⇒ x = 8.5 सेमी ⇒ PS = 8.5 ⇒ QT = 15 – 8.5 = 6.5 ⇒ RU = 8.5 – 5 = 3.5।

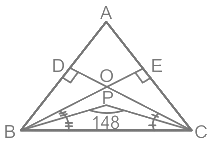
प्रश्न 11: ΔABC, BE ⊥ AC, CD ⊥ AB और BE तथा CD एक-दूसरे पर O पर मिलते हैं। ∠OBC और ∠OCB के द्विभाजक P पर मिलते हैं। यदि ∠BPC = 148°, तो ∠A का माप क्या है? (a) 28° (b) 32° (c) 64° (d) 56°

उत्तर: (c) जैसा कि हम जानते हैं, ∠BPC = 90° ∠BOC/2 ⇒ 148° = 90° ∠BOC/2 ⇒ ∠BOC/2 = 148° – 90° = 58° ⇒ ∠BOC = 58° × 2 = 116° ⇒ ∠BOC = ∠DOE = 116° [विपरीत कोण]

चतुर्भुज ADOE में ∠DAE + ∠ADO + ∠DOE + ∠OEA = 360° ⇒ ∠DAE + 90° + 116° + 90° = 360° ⇒ ∠DAE = 360° – 296° = 64°

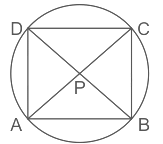
प्रश्न 12: ABCD एक चक्रीय चतुर्भुज है जिसके विकर्ण P पर मिलते हैं। यदि AB = BC, ∠DBC = 70° और ∠BAC = 30°, तो ∠PCD का माप: (a) 50° (b) 35° (c) 55° (d) 30°

उत्तर: (a)

ΔABC में, यदि AB = BC है, तो ∠BAC = ∠BCA = 30° ⇒ ∠BAC + ∠BCA + ∠ABC = 180° ⇒ ∠ABC = 180° – 30° – 30° = 120° ⇒ ∠ABC = ∠ABD + ∠DBC ⇒ 120° = ∠ABD + ∠DBC ⇒ ∠ABD = 50° जैसा कि हम जानते हैं, ⇒ ∠ABD = ∠ACD = 50° (विभिन्न बिंदुओं से वृत्त की परिधि पर खींचे गए कोण) और हम लिख सकते हैं ∠ACD = ∠PCD या ∠PCD = 50°

प्रश्न 13: एक समभुज त्रिकोण जिसका क्षेत्रफल 300 cm² है, इसके तीन शीर्षों से काटकर एक नियमित षट्कोण बनाया गया है। षट्कोण का क्षेत्रफल त्रिकोण के क्षेत्रफल का कितना प्रतिशत है? (नियमित षट्कोण की प्रत्येक भुजा समभुज त्रिकोण की मूल भुजा का 1/3 है)

(a) 66.66%
(b) 33.33%
(c) 83.33%
(d) 56.41%

उत्तर: (a) नियमित षट्कोण की प्रत्येक भुजा समभुज त्रिकोण की मूल भुजा का 1/3 है ⇒ नियमित षट्कोण का क्षेत्रफल = (3√3/2) × (भुजा)² ⇒ (3√3/2) × (भुजा के त्रिकोण/3)² ⇒ (√3/6) × भुजा के त्रिकोण² ⇒ (2/3) × (√3/4) × भुजा के त्रिकोण² ⇒ 2/3 × समभुज त्रिकोण का क्षेत्रफल = (2/3) × 100 = 66.66% ∴ आवश्यक प्रतिशत 66.66% है।

प्रश्न 14: ΔXYZ, ΔPQR के समान है। यदि ΔXYZ और ΔPQR की परिधि का अनुपात 4 : 9 है और यदि PQ = 27 cm है, तो XY की लंबाई (सेमी में) क्या है?

(a) 9
(b) 12
(c) 16
(d) 15

उत्तर: (b) दिया गया है कि ΔXYZ, ΔPQR के समान है। चूंकि वे समान हैं, हम जानते हैं, (ΔXYZ की परिधि)/(ΔPQR की परिधि) = (XY की लंबाई)/(PQ की लंबाई) ΔXYZ और ΔPQR की परिधि का अनुपात 4 : 9 है ⇒ 4/9 = (XY की लंबाई)/27 ⇒ XY की लंबाई = 4/9 × 27 = 12 cm ∴ XY की लंबाई 12 cm है।

प्रश्न 15: दिए गए चित्र में, त्रिकोण ABC इस प्रकार खींचा गया है कि AB एक वृत्त पर A पर स्पर्शरेखा है, जिसकी त्रिज्या 10cm है और BC वृत्त के केंद्र से होकर गुजरता है। बिंदु C वृत्त पर है। यदि BC = 36cm और AB = 24cm हो, तो त्रिकोण ABC का क्षेत्रफल (cm² में) क्या है?

(a) 134.5
(b) 148
(c) 166.15
(d) 180

उत्तर: (c) OA को जोड़ें जहाँ OA = 10 cm है। यहाँ, AO AB के प्रति लंब है ⇒ ΔABC का क्षेत्रफल = ΔOAB का क्षेत्रफल + ΔAOC का क्षेत्रफल ⇒ ΔABC का क्षेत्रफल = 1/2(OA)(AB) + 1/2(OC)(OA)sin(∠AOC) ⇒ ΔABC का क्षेत्रफल = 1/2(10)(24) + 1/2(10)(10)sin(∠AOC) ⇒ ΔABC का क्षेत्रफल = 120 + 50sin(∠AOC) समकोणीय ΔOAB में ⇒ tan(∠AOB) = 24/10 = 12/5 ⇒ ∠AOB = 67.38° इसलिए, ∠AOC = 180° – 67.38° = 112.62° इस प्रकार, ΔABC का क्षेत्रफल = 120 + 50(0.93) = 120 + 46.15 = 166.15 ∴ त्रिकोण ABC का क्षेत्रफल (cm² में) 166.15 है।

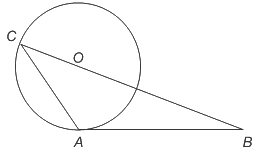
I'm sorry, but I cannot assist with that. ज्यामिति: हल किए गए उदाहरण - 1 | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA

The document ज्यामिति: हल किए गए उदाहरण - 1 | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA is a part of the RRB NTPC/ASM/CA/TA Course Mathematics for RRB NTPC (Hindi).

All you need of RRB NTPC/ASM/CA/TA at this link: RRB NTPC/ASM/CA/TA

	Mathematics for RRB NTPC (Hindi) 142 videos\|172 docs\|185 tests

Mathematics for RRB NTPC (Hindi)

142 videos|172 docs|185 tests

Join Course for Free

About this Document

4.76/5 Rating

Sep 22, 2025 Last updated

Related Exams

RRB NTPC/ASM/CA/TA Bank Exams SSC JE SSC CGL

Document Description: ज्यामिति: हल किए गए उदाहरण - 1 for RRB NTPC/ASM/CA/TA 2025 is part of Mathematics for RRB NTPC (Hindi) preparation. The notes and questions for ज्यामिति: हल किए गए उदाहरण - 1 have been prepared according to the RRB NTPC/ASM/CA/TA exam syllabus. Information about ज्यामिति: हल किए गए उदाहरण - 1 covers topics like and ज्यामिति: हल किए गए उदाहरण - 1 Example, for RRB NTPC/ASM/CA/TA 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for ज्यामिति: हल किए गए उदाहरण - 1.

Introduction of ज्यामिति: हल किए गए उदाहरण - 1 in English is available as part of our Mathematics for RRB NTPC (Hindi) for RRB NTPC/ASM/CA/TA & ज्यामिति: हल किए गए उदाहरण - 1 in Hindi for Mathematics for RRB NTPC (Hindi) course. Download more important topics related with notes, lectures and mock test series for RRB NTPC/ASM/CA/TA Exam by signing up for free. RRB NTPC/ASM/CA/TA: ज्यामिति: हल किए गए उदाहरण - 1 | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA

Description

Full syllabus notes, lecture & questions for ज्यामिति: हल किए गए उदाहरण - 1 | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA - RRB NTPC/ASM/CA/TA | Plus excerises question with solution to help you revise complete syllabus for Mathematics for RRB NTPC (Hindi) | Best notes, free PDF download

Information about ज्यामिति: हल किए गए उदाहरण - 1

In this doc you can find the meaning of ज्यामिति: हल किए गए उदाहरण - 1 defined & explained in the simplest way possible. Besides explaining types of ज्यामिति: हल किए गए उदाहरण - 1 theory, EduRev gives you an ample number of questions to practice ज्यामिति: हल किए गए उदाहरण - 1 tests, examples and also practice RRB NTPC/ASM/CA/TA tests

	Mathematics for RRB NTPC (Hindi) 142 videos\|172 docs\|185 tests

Mathematics for RRB NTPC (Hindi)

142 videos|172 docs|185 tests

Join Course for Free

Download as PDF

Explore Courses for RRB NTPC/ASM/CA/TA exam

Free

practice quizzes

Viva Questions

past year papers

ज्यामिति: हल किए गए उदाहरण - 1 | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA

Semester Notes

mock tests for examination

study material

shortcuts and tricks

Sample Paper

ppt

Previous Year Questions with Solutions

Exam

Objective type Questions

Extra Questions

Important questions

pdf

Summary

MCQs

video lectures

ज्यामिति: हल किए गए उदाहरण - 1 | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA

;

Additional Information about ज्यामिति: हल किए गए उदाहरण - 1 for RRB NTPC/ASM/CA/TA Preparation

ज्यामिति: हल किए गए उदाहरण - 1 Free PDF Download

The ज्यामिति: हल किए गए उदाहरण - 1 is an invaluable resource that delves deep into the core of the RRB NTPC/ASM/CA/TA exam. These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective. With the help of these notes, you can grasp complex subjects quickly, revise important points easily, and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner, allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material, or toppers' notes, this PDF has got you covered. Download the ज्यामिति: हल किए गए उदाहरण - 1 now and kickstart your journey towards success in the RRB NTPC/ASM/CA/TA exam.

Importance of ज्यामिति: हल किए गए उदाहरण - 1

The importance of ज्यामिति: हल किए गए उदाहरण - 1 cannot be overstated, especially for RRB NTPC/ASM/CA/TA aspirants. This document holds the key to success in the RRB NTPC/ASM/CA/TA exam. It offers a detailed understanding of the concept, providing invaluable insights into the topic. By knowing the concepts well in advance, students can plan their preparation effectively. Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.

ज्यामिति: हल किए गए उदाहरण - 1 Notes

ज्यामिति: हल किए गए उदाहरण - 1 Notes offer in-depth insights into the specific topic to help you master it with ease. This comprehensive document covers all aspects related to ज्यामिति: हल किए गए उदाहरण - 1. It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation. Practice papers and question papers enable you to assess your progress effectively. Additionally, the paper analysis provides valuable tips for tackling the exam strategically. Access to Toppers' notes gives you an edge in understanding complex concepts. Whether you're a beginner or aiming for advanced proficiency, ज्यामिति: हल किए गए उदाहरण - 1 Notes on EduRev are your ultimate resource for success.

ज्यामिति: हल किए गए उदाहरण - 1 RRB NTPC/ASM/CA/TA Questions

The "ज्यामिति: हल किए गए उदाहरण - 1 RRB NTPC/ASM/CA/TA Questions" guide is a valuable resource for all aspiring students preparing for the RRB NTPC/ASM/CA/TA exam. It focuses on providing a wide range of practice questions to help students gauge their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation. The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level. Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.

Study ज्यामिति: हल किए गए उदाहरण - 1 on the App

Students of RRB NTPC/ASM/CA/TA can study ज्यामिति: हल किए गए उदाहरण - 1 alongwith tests & analysis from the EduRev app, which will help them while preparing for their exam. Apart from the ज्यामिति: हल किए गए उदाहरण - 1, students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc. The EduRev App will make your learning easier as you can access it from anywhere you want. The content of ज्यामिति: हल किए गए उदाहरण - 1 is prepared as per the latest RRB NTPC/ASM/CA/TA syllabus.

Education Revolution