टिप्स और ट्रिक्स: साइलोज़िज़्म | General Intelligence & Reasoning for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA PDF Download
सिलॉजिज़म शॉर्टकट्स
मैं बुनियादी सिलॉजिज़म शब्दावली को समझाने से शुरू करूंगा, जिसके बाद व्यावहारिक उदाहरण दिए जाएंगे।
- 1. सभी
- 2. कुछ
- 3. कोई नहीं
केस # सभी - कुछ
कल्पना कीजिए! आपके पास 1000 $ हैं। आपके एक दोस्त को अपने बिल का भुगतान करने के लिए 600 $ चाहिए। वह आपसे पैसे उधार लेना चाहता है। वह आपके पास आता है और कहता है, "क्या आपके पास 600 $ हैं?" आप क्या कहेंगे, "बिल्कुल हाँ!"। भले ही वह 1 $ या 999 $ मांगता है। आपका जवाब हमेशा "हाँ!" होगा। तो कुल मिलाकर आपके पास 1000 $ हैं, जिसे हम "सभी" कहते हैं, या आपके पास जो भी पैसे हैं। और आपके दोस्त को कुछ पैसे चाहिए, जैसे कि यहां 600 $ या यह 1 $ या 999 $ भी हो सकता है, और हम इसे कहते हैं कि वह पैसे का एक हिस्सा मांग रहा है, या "कुछ"। इसलिए "सभी" के मामले में, "कुछ" हमेशा सही है।
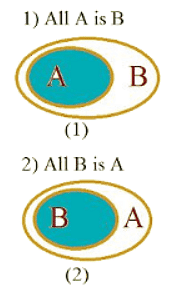
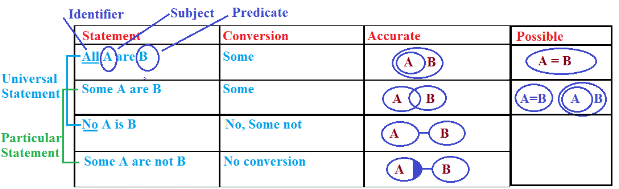
उदाहरण: कथन: सभी A B हैं।
निष्कर्ष: सभी A B हैं ✓ कुछ A B हैं ✓ कुछ B A हैं ✓ कुछ A B नहीं हैं ✘ कुछ B A नहीं हैं ✘ अब यहां हम देख सकते हैं कि A में संख्याओं का एक सेट है। इसलिए हम इसे सेट A कहते हैं और B के लिए 'सेट B' कहते हैं। A में सभी संख्याएँ B में शामिल हैं, इसलिए सभी A B हैं, यह सत्य है। लेकिन सभी B A में नहीं हैं या A द्वारा शामिल नहीं हैं, इसलिए सभी B A → गलत है। अब समझते हैं कि कैसे सभी A B → सत्य है लेकिन सभी B A → गलत है। मान लीजिए बॉक्स A और बॉक्स B हैं। यहां हम देख सकते हैं कि बॉक्स B बॉक्स A के अंदर है। इसलिए बॉक्स B को बॉक्स A में फिट किया जा सकता है लेकिन बॉक्स A को बॉक्स B में फिट नहीं किया जा सकता।
केस # कुछ - कुछ नहीं

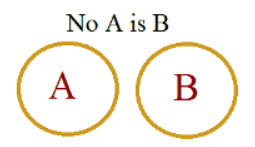

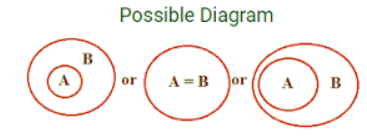
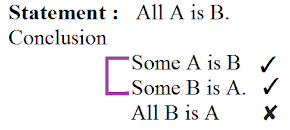
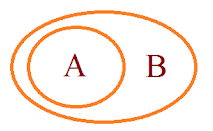

केस # कुछ - कुछ नहीं
मान लें कि आपने परीक्षा दी है और आप कुछ अंक प्राप्त करने में सफल रहे हैं, जिसका अर्थ है कि आपको कुछ अंक मिले हैं और कुछ नहीं। भले ही आप 99% अंक के साथ परीक्षा पास कर लें, फिर भी आप 1% अंक चूक गए हैं। इसलिए 99% भी उसी मामले में आता है, और 1% भी कुछ मामलों में गिना जाता है। इस प्रकार 'कुछ' मामले में 'कुछ नहीं' सत्य है।

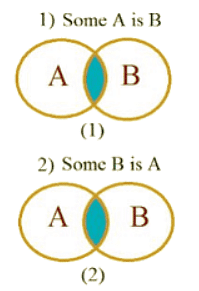
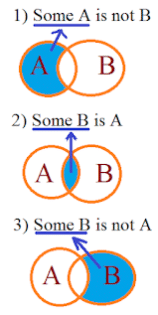
बयान: कुछ A, B हैं
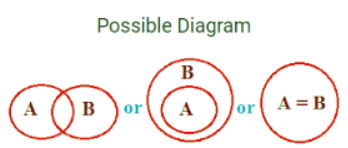
निष्कर्ष: सभी B, A हैं ✘ कुछ B, A हैं ✓ कोई A, B नहीं है ✘
बयान: कुछ A, B नहीं हैं
व्याख्या: यहाँ हम देखते हैं कि सेट A और सेट B में कुछ सामान्य मान हैं, इसलिए हम कह सकते हैं कि कुछ A, B हैं और कुछ B, A हैं। लेकिन वहाँ कुछ मान भी हैं जो A और B दोनों में सामान्य नहीं हैं। इसलिए हम यह भी कह सकते हैं कि कुछ A, B नहीं हैं और कुछ B, A नहीं हैं।

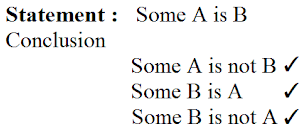
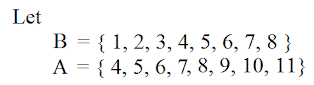
केस # नहीं - कुछ नहीं
केस # संख्या - कुछ नोट्स
मान लीजिए आपके पास जेब में कोई पैसा नहीं है। तो यदि आपके पास पैसा नहीं है, इसका अर्थ भी यह है कि कुछ पैसा आपकी जेब में नहीं है। "नहीं" होना का अर्थ भी "कुछ नहीं" है।

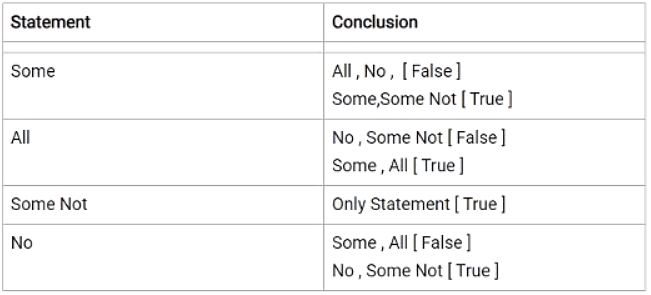
सिलोजिज़्म हल करते समय याद रखने योग्य बातें
- किसी भी कथन में कुछ भी संभव है। जैसे कि कुछ पेन फैन हैं। कोई फैन हीटर नहीं है। नकारात्मक उत्तर कभी नहीं होगा।
सरल मामला
उदाहरण
उदाहरण 1: कथन: कुछ A B हैं, कुछ B C हैं, सभी C D हैं

निष्कर्ष: कुछ A D नहीं हैं ✘ कुछ B D हैं ✓ कुछ A C नहीं हैं ✘
उदाहरण 2: कथन: कुछ A B हैं, कुछ B C हैं, कोई C D नहीं है

निष्कर्ष: कुछ B D नहीं हैं ✘ कुछ D B नहीं हैं ✘ कुछ A C नहीं हैं ✘
उदाहरण 3: कथन: सभी A B हैं, सभी A C हैं, सभी A D हैं, कोई D E नहीं है
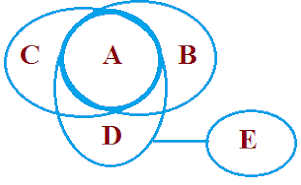
निष्कर्ष: कुछ B E नहीं हैं ✓ कुछ A E नहीं हैं ✓ कोई C E नहीं है ✓ कोई A E नहीं है ✓ कोई E A नहीं है ✓
उदाहरण 4: कथन: कुछ A B हैं, कुछ B C हैं, कुछ C D हैं, कुछ D E हैं
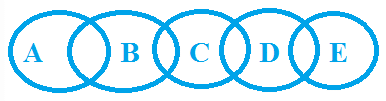
निष्कर्ष: कुछ C A नहीं हैं ✘ कुछ B D नहीं हैं ✘ कुछ A E हैं ✘ सभी B D हैं ✘ कोई A E नहीं है ✘ कुछ C A हैं ✘ सभी B E हैं ✘ कोई B E नहीं है ✘
'या या' और 'न तो न'
पूरक जोड़ी
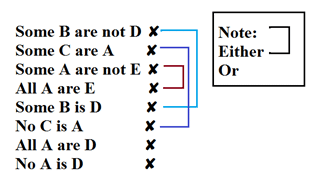
- यदि एक निष्कर्ष सकारात्मक है और दूसरा नकारात्मक है। नहीं - कुछ कुछ - कुछ नहीं सभी - कुछ नहीं
- एक ही विषय और एक ही विशेषण मौजूद हैं
- और दोनों निष्कर्ष खींचने में असमर्थ हैं तो उत्तर होगा या या
उदाहरण 1: कथन: सभी A B हैं, सभी A C हैं, सभी A D हैं, कोई D E नहीं है, कुछ F C हैं। निष्कर्ष
उदाहरण 2: कथन: कुछ A B हैं, कुछ B C हैं, कुछ C D हैं, कुछ D E हैं
अपवाद
- सार्वभौमिक निष्कर्ष (जैसे 'सभी और कोई नहीं') के मामले में पूरक जोड़ी काम नहीं करती है।
- इस प्रकार के प्रश्न में "न तो न" होता है।
उदाहरण 3: कथन: कुछ A B हैं, सभी B C हैं, कोई C D नहीं है।
निष्कर्ष: कुछ A D नहीं हैं ✘ कोई B D नहीं है ✘ कुछ A C हैं ✘ कुछ D B हैं ✘
उदाहरण 4: कथन: सभी A B हैं, कोई B C नहीं है, सभी C D हैं।
निष्कर्ष: कुछ A D नहीं हैं ✘ कोई D B नहीं है ✘ कोई A C नहीं है ✓ कोई A D नहीं है ✓ कोई D A नहीं है ✘
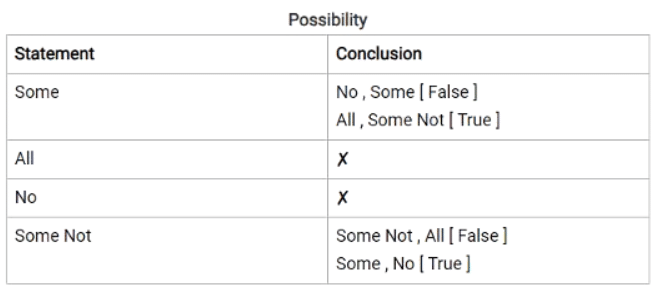
संभावना
उदाहरण: कथन: कुछ A B हैं, कुछ B C हैं। निष्कर्ष: व्याख्या (सरल मामला A, B और C): मान लीजिए A, B और C तीन व्यक्ति हैं। A और B एक-दूसरे को जानते हैं। B और C एक-दूसरे को जानते हैं, लेकिन B दोनों को जानता है। अब, क्या A C के बारे में बात करेगा? उत्तर है 'नहीं! न तो सकारात्मक और न ही नकारात्मक' क्योंकि वह उसे नहीं जानता। इसलिए निष्कर्ष C गलत है। संभावना के मामले (निष्कर्ष: D, E और F): अब निष्कर्ष E पर ध्यान दें। मान लीजिए कि आपके घर के बाहर बारिश हो रही है और कोई आपके पास आता है और कहता है कि आज बारिश होने की संभावना है। आप उससे क्या कहेंगे, 'पागल!'। वही स्थिति यहाँ है। चित्र देखकर यह स्पष्ट है कि कुछ B A हैं, तो हम इसे 'संभावित' कैसे कह सकते हैं, जो वास्तव में है। इसलिए संभावना निष्कर्ष को गलत या झूठा बनाती है। इसलिए निष्कर्ष E गलत है। अब निष्कर्ष F के बारे में बात करें जो कहता है कि कुछ A C नहीं हैं, जिसे हम नहीं जानते लेकिन यह कहता है कि यह 'संभावना' है, इसलिए कुछ भी संभव हो सकता है, जो हमारे कथन को गलत या विरोधाभासी नहीं बनाता। अगर हम इसे नीचे की तरह बनाते हैं:
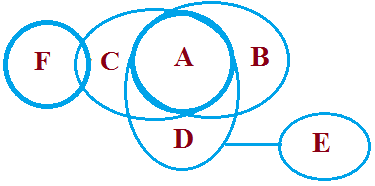

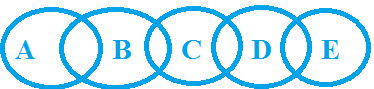

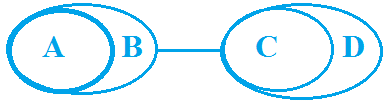

यहाँ हम संभावनाओं के बारे में बात कर रहे हैं, जो कुछ भी हो सकती हैं, विशेष रूप से जो हमारे कथन के विपरीत नहीं हैं। इसलिए F जो साधारण मामले में False था, लेकिन जब हम संभावनाओं के बारे में बात करते हैं तो यह true होने लगती है। आइए इसके लिए एक और उदाहरण लें।
मान लीजिए कि आपके घर के बाहर आसमान में बादल हैं। कोई आपसे कहता है, "आज बारिश होने की संभावना है।" अब आपके पास यह जानने का कोई तरीका नहीं है कि आज बारिश होगी या नहीं। तो आप कह सकते हैं, "भाई! यह संभव है।" यहाँ आप नकारात्मकता के बारे में बात नहीं कर सकते हैं क्योंकि सिलोगिज्म में नकारात्मक उत्तर कभी नहीं होता।
एक कथन में ऐसे शब्द जिन्हें संभावनाएँ कहा जाता है:
- हो सकता है
- शायद / संभवतः
- अवसर
- घटित होता है
- संभावित है
एक कथन में ऐसे शब्द जिन्हें निश्चितताएँ कहा जाता है:
- कभी नहीं हो सकता
- हो सकता है
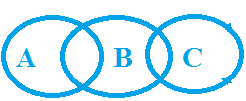
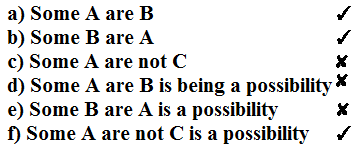


|
127 docs|197 tests
|




















