महत्वपूर्ण सूत्र: द्विघात समीकरण | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA PDF Download
क्वाड्रेटिक समीकरण की परिभाषा
क्वाड्रेटिक समीकरण एक एकल चर में बहुपद समीकरण का एक रूप है, जिसे सामान्यतः \"x\" के रूप में दर्शाया जाता है, और इसे निम्नलिखित सामान्य रूप में प्रस्तुत किया जा सकता है: ax² + bx + c = 0। इस प्रतिनिधित्व में, \"a,\" \"b,\" और \"c\" स्थिरांक हैं, जिसमें यह शर्त है कि \"a\" 0 के बराबर नहीं होना चाहिए।
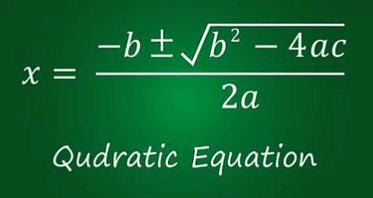
क्वाड्रेटिक समीकरण का सूत्र और परिभाषाएँ
- एक समीकरण जिसमें चर का उच्चतम घातांक वर्ग होता है।
- क्वाड्रेटिक समीकरण का सामान्य रूप है: ax² + bx + c = 0
- जहाँ, x अज्ञात चर है और a, b, c संख्या गुणांक हैं।
क्वाड्रेटिक समीकरण के सूत्र
- यदि ax² + bx + c = 0 एक क्वाड्रेटिक समीकरण है, तो x का मान निम्नलिखित सूत्र द्वारा दिया गया है।
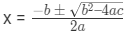
क्वाड्रेटिक समीकरण का सूत्र और क्वाड्रेटिक प्रश्नों की विधि
1. फैक्टराइजेशन
यह क्वाड्रेटिक समीकरणों को हल करने का एक बहुत सरल तरीका है। फैक्टराइजेशन से 2 रेखीय समीकरण मिलते हैं।
उदाहरण के लिए: x² - 3x - 4 = 0 यहाँ, a = 1, b = -3 और c = -4। अब, दो संख्याओं को खोजें जिनका गुणनफल -4 और योग 3 है। इसलिए, संख्याएँ 4 और -1 हैं। इसलिए, दो गुणांक होंगे 4 और -1।
2. स्क्वायर पूरा करने की विधि
हर क्वाड्रेटिक प्रश्न में हमेशा एक वर्गीय पद होता है। यदि हम समानता के चिन्ह के साथ दो वर्गीय पद प्राप्त कर सकते हैं, तो हम रेखीय समीकरण प्राप्त कर सकते हैं। मध्य पद को ‘b’ कहा जाता है और इसे (b/2)² द्वारा विभाजित किया जाता है। उदाहरण के लिए: - x² + 4x + 4 यहाँ x² = 1, b = 4 (x - 2)² = 3, दोनों पक्षों का वर्ग लें।
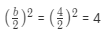
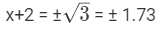
इसलिए, x = -0.27 या -3.73
गुणात्मक समीकरणों के सूत्र और याद रखने के लिए मुख्य बिंदु
गुणात्मक समीकरणों को हल करते समय याद रखने के लिए अन्य मूलभूत अवधारणाएँ हैं:
1. जड़ों का स्वभाव
- जड़ों का स्वभाव निर्धारित करता है कि समीकरण की दी गई जड़ें वास्तविक, काल्पनिक, सांकेतिक या अवास्तविक हैं। मूल सूत्र है b² – 4ac। इस सूत्र को डिस्क्रिमिनेंट या D भी कहा जाता है। जड़ों का स्वभाव D के मान पर निर्भर करता है। जड़ों के स्वभाव को निर्धारित करने के लिए शर्तें हैं:
- यदि D < />, तो दी गई जड़ें काल्पनिक हैं।
- यदि D = 0, तो दी गई जड़ें वास्तविक और समान हैं।
- यदि D > 0, तो जड़ें वास्तविक और असमान हैं।
- इसके अलावा, यदि D > 0 है और समीकरण एक पूर्ण वर्ग है, तो दी गई जड़ें सांकेतिक हैं, अन्यथा वे अवास्तविक हैं।
2. जड़ों का योग और गुणनफल
- किसी भी दी गई समीकरण के लिए जड़ों का योग हमेशा (Α + Β) होगा और जड़ों का गुणनफल (Α * Β) होगा। इस प्रकार, मानक गुणात्मक समीकरण को इस प्रकार भी लिखा जा सकता है: x² – (Α + Β)x + (Α * Β) = 0
3. गुणात्मक समीकरण बनाना
- जब समीकरण की जड़ें दी जाती हैं या जड़ों का गुणनफल और योग दिए जाते हैं, तब समीकरण बनाया जा सकता है।
गुणात्मक समीकरणों पर प्रश्न
प्रश्न 1: निम्नलिखित में से गुणात्मक समीकरण का सामान्य रूप कौन सा है? (a) x² + 3x – 2 = 0 (b) 3x + 2 = 5 (c) 2x – 4 = 0 (d) 5x² – 7x = 3 उत्तर: (a) गुणात्मक समीकरण का सामान्य रूप ax² + bx + c = 0 है, जहाँ “a,” “b,” और “c” स्थिरांक हैं। विकल्प A इस प्रारूप का पालन करता है, जो एक गुणात्मक समीकरण का प्रतिनिधित्व करता है।
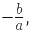
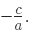
प्रश्न 2: निम्नलिखित में से कौन सा विधि द्विघात समीकरण x² – 6x + 9 = 0 को हल करने के लिए सबसे उपयुक्त है? (क) गुणन (ख) द्विघात सूत्र (ग) वर्ग पूरा करना (घ) ग्राफिकल विश्लेषण उत्तर: (ग) द्विघात समीकरण x² – 6x + 9 = 0 एक पूर्ण वर्ग त्रैणम है, और वर्ग पूरा करना इसे हल करने का सबसे प्रभावी तरीका है। इस विधि में समीकरण को एक वर्ग बाइनोमियल में परिवर्तित करना शामिल है, जिससे समाधान खोजना आसान हो जाता है।
प्रश्न 3: निम्नलिखित में से कौन सा द्विघात समीकरण जटिल मूल (complex roots) रखता है? (क) 2x² + 4x + 5 = 0 (ख) x² + 6x + 9 = 0 (ग) 3x² – 6x + 3 = 0 (घ) 5x² – 10x + 5 = 0 उत्तर: (क) एक द्विघात समीकरण का विभाजक (discriminant) (Δ) इसके मूल (roots) की प्रकृति को निर्धारित करता है। यदि Δ < 0,="" तो="" समीकरण="" के="" जटिल="" मूल="" होते="" हैं।="" विकल्प="" (क)="" के="" लिए,="" विभाजक="" 4²="" –="" 4(2)(5)="16" –="" 40="-24" है,="" जो="" नकारात्मक="" है।="" इसलिए,="" द्विघात="" समीकरण="" 2x²="" +="" 4x="" +="" 5="0" के="" जटिल="" मूल="" />
प्रश्न 4: द्विघात समीकरण 2x² – 5x + 3 = 0 का विभाजक क्या है? (क) 1 (ख) -11 (ग) -19 (घ) 11 उत्तर: (ग) एक द्विघात समीकरण ax² + bx + c = 0 का विभाजक (Δ) इस अभिव्यक्ति द्वारा दिया जाता है: Δ = b² – 4ac। दिए गए समीकरण के गुणांक को प्रतिस्थापित करते हुए, हमें Δ = (-5)² – 4(2)(3) = 25 – 24 = 1 मिलता है। इसलिए, विभाजक 1 है।
प्रश्न 5: द्विघात समीकरण 2x² + 5x – 3 = 0 के मूल क्या हैं? (क) x = -3 और x = 1/2 (ख) x = 3 और x = -1/2 (ग) x = -3 और x = -1/2 (घ) x = 3 और x = 1/2 उत्तर: (क) द्विघात समीकरण को इस प्रकार गुणित किया जा सकता है: (2x – 3)(x + 1) = 0। प्रत्येक गुणांक को शून्य के बराबर रखने पर हमें 2x – 3 = 0 और x + 1 = 0 मिलता है। प्रत्येक समीकरण में “x” के लिए हल करते हुए, हमें x = 3/2 और x = -1 मिलता है। इसलिए, मूल हैं x = -3 और x = 1/2।
|
142 videos|172 docs|185 tests
|















