संक्षेप: संख्याओं की गणना | General Intelligence & Reasoning for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA PDF Download

आकृतियों की गिनती

आकृतियों की गिनती में, आपके पास एक आकार या आकृति होती है। दिए गए आकार से आपको एक ज्ञात आकृति की पहचान करनी होती है और यह गिनना होता है कि वह आकृति कितनी बार मौजूद है। उदाहरण के लिए, निम्नलिखित आकृति पर विचार करें:

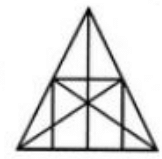
एक सामान्य आकृतियों की गिनती का प्रश्न आपसे पूछेगा कि आप यहाँ कितने त्रिकोण पहचान सकते हैं? यह आसान लग सकता है लेकिन जैसे कि आप देखेंगे, यह बहुत जटिल हो सकता है! चलिए त्रिकोण के विभिन्न शीर्ष बिंदुओं का नाम देते हैं और आकृति के भीतर या त्रिकोण पर हर इंटरसेक्शन बिंदु को भी नामित करते हैं। इससे हमें आकृति में त्रिकोणों की संख्या पहचानने और ट्रैक करने में मदद मिलेगी।

एक आसान तरीका

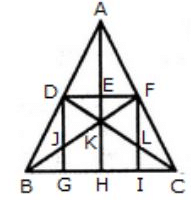
कुछ त्रिकोण ऐसे हैं जो आसानी से पहचाने जा सकते हैं। ये त्रिकोण हैं (A D E), (A E F), (D E K), (E F K), (D J K), (F L K), (D J B), (F L C), (B J G), और (L I C) जैसा कि आप आकृति में देख सकते हैं। इन त्रिकोणों की संख्या दस है। अन्य त्रिकोण हैं जो दो भागों या दो घटकों से मिलकर बने हैं। ये त्रिकोण हैं (A D F), (A F K), (D F K), (A D K), (D K B), (F C K), (B K H), (K H C), (D G B), और (F I C)। इसी प्रकार, हम उन त्रिकोणों को भी ढूंढ सकते हैं जो तीन घटकों से बने हैं। वे त्रिकोण हैं (D F J), और (D F L)। इसके अलावा, चार घटकों वाले त्रिकोण हैं (A B K), (A C K), (B F I), (C D G), (D F B), (D F C) और (B K C)। इस प्रकार, इनकी संख्या सात है। पांच घटकों वाले कोई त्रिकोण नहीं हैं। अब हम उन त्रिकोणों को भी पहचान सकते हैं जो छह घटकों से बने हैं। वे त्रिकोण हैं (A B H), (A C H), (A B F), (A C D), (B F C), और (C D B)। इस प्रकार, उनकी संख्या छह है। अंत में, हम देखते हैं कि सात, आठ, नौ, दस या ग्यारह घटकों वाले कोई त्रिकोण नहीं हैं। और केवल एक त्रिकोण है जिसमें सभी बारह घटक हैं यानी त्रिकोण A B C। इसलिए, उपरोक्त आकृति में कुल त्रिकोणों की संख्या है 10 + 10 + 2 + 7 + 6 + 1 = 36।

हल किए गए उदाहरण

उदाहरण 1: निम्नलिखित चित्र में त्रिकोणों की संख्या क्या है?

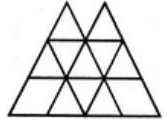
उत्तर: पहले कदम के रूप में, हमें हर एक शीर्ष बिंदु और रेखाओं के इंटरसेक्शन बिंदुओं को निम्नलिखित चित्र के अनुसार लेबल करना चाहिए:

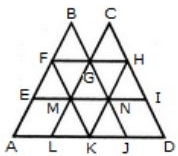
अब हम उन त्रिकोणों को देखेंगे जो चित्र में एकल घटक द्वारा बनते हैं। ये त्रिकोण हैं (B F G), (C G H), (E F M), (F M G), (G M N), (G H N), (H N I), (L M K), (M N K), और (K N J)। इनकी संख्या दस है। दो घटकों को जोड़ने पर त्रिकोण नहीं बनेगा, इसलिए ऐसे कोई त्रिकोण नहीं हैं। तीन घटकों वाले त्रिकोण हैं (F A K) और (H K D)। ये दो हैं। चार भागों वाले त्रिकोण हैं (B E N), (C M I), (G L J), और (F H K), इस प्रकार ये चार हैं। इसी तरह, हम देखते हैं कि पांच, छह, और सात घटक त्रिकोण नहीं बनाएंगे। अब हम आठ घटकों से बने त्रिकोणों की संख्या की गणना करते हैं। ये हैं (B A J), और (O L D)। यहाँ घटकों की अधिकतम संख्या है। इसलिए यहाँ कुल त्रिकोणों की संख्या है 10 + 2 + 4 + 2 = 18। इस प्रकार, ऊपर दिए गए चित्र में 18 त्रिकोण हैं।

उदाहरण 2: निम्नलिखित चित्र में त्रिकोणों की संख्या क्या है?

उत्तर: पहले कदम के रूप में, हमें दिए गए चित्र में हर एक शीर्ष बिंदु और इंटरसेक्शन बिंदुओं को निम्नलिखित चित्र के अनुसार लेबल करना चाहिए:

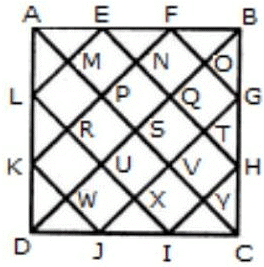
अब जब हमने लेबलिंग का ध्यान रखा है, तो आइए गणना पर ध्यान दें। यहाँ हमारे पास बड़े वर्ग के किनारों पर छोटे त्रिकोणीय आकार हैं और बीच में छोटे वर्ग हैं। जो त्रिकोण आसानी से देखे जा सकते हैं वे हैं (A M L), (L R K), (K W D), (D W J), (J X I), (I Y C), (C Y H), (H T G), (G O B), (B O F), (F N E) और त्रिकोण (E M A)। इनकी संख्या बारह है। अब दो घटकों से बने त्रिकोणों की गणना करें। ये हैं त्रिकोण (A E L), (K D J), (H I C) और (F B G)। इनकी संख्या चार है। इसके अतिरिक्त हम तीन घटकों से बने त्रिकोणों की संख्या गिन सकते हैं। ये हैं (A P F), (E Q B), (B Q H), (G V C), (C V J), (I U D), (D U L) और (K P A)। इनकी संख्या आठ है। इसी तरह हम देखते हैं कि त्रिकोण (A S B), (B S G), (C S D), (D S A), (A K F), (E B H), (G C J) और (I D L) छह घटकों से बने हैं। और त्रिकोण (A D B), (A B C), (B C D) और (C D A) बारह घटकों से बने हैं। इस प्रकार चित्र में कुल त्रिकोणों की संख्या है 12 + 4 + 8 + 8 + 4 = 36।

अभ्यास प्रश्न

प्रश्न 1: निम्नलिखित आकृति बनाने के लिए उपयोग की जाने वाली सीधी रेखा खंडों की न्यूनतम संख्या क्या है?

(क) 36 (ख) 46 (ग) 66 (घ) 14 (च) 21 उत्तर: (घ) 14