संख्याओं की श्रेणियों के प्रकार | General Intelligence & Reasoning for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA PDF Download

परिचय

संख्याओं की श्रृंखला एक प्रकार का अनुक्रम है, जिसमें कुछ संख्याएँ गलती से संख्याओं की श्रृंखला में डाल दी जाती हैं और कुछ संख्या उस श्रृंखला में गायब होती है। हमें पहले निरीक्षण करना होता है और फिर उस श्रृंखला के लिए सही संख्या को ढूंढना होता है।

एक अनुक्रम उन संख्याओं की सूची है जो एक विशेष क्रम में लिखी जाती हैं। उदाहरण: 1, 4, 9, 16, 25, 36……..

संख्याओं की श्रृंखला पर प्रश्न अधिकांश MBA प्रवेश परीक्षाओं में सामान्य होते हैं। इस विषय पर प्रश्न उन संख्यात्मक अनुक्रमों पर आधारित होते हैं जो एक तार्किक पैटर्न का पालन करते हैं। ये पैटर्न बुनियादी गणितीय अवधारणाओं पर आधारित होते हैं। विभिन्न प्रकार की श्रृंखलाएँ और उनके उदाहरण नीचे दिए गए हैं:

(क) प्राइम नंबर श्रृंखला

यह एक श्रृंखला है जो प्राइम संख्याओं पर आधारित होती है और सामान्यतः एक संख्या गायब होती है या गलत स्थान पर होती है।

उदाहरण 1: श्रृंखला 3, 5, 7, 11, 13, ……... का अगला पद खोजें। समाधान:

► उपरोक्त श्रृंखला में सभी संख्याएँ विषम हैं, लेकिन 7 के बाद 9 नहीं है। ► इसलिए, हमें किसी अन्य पैटर्न की खोज करनी होगी। ► हम देखते हैं कि सभी संख्याएँ प्राइम हैं; इसलिए यह एक प्राइम नंबर श्रृंखला है; इसलिए अगला पद 17 होगा।

उदाहरण 2: प्रश्न चिह्न के स्थान पर पद ढूंढें 8, 10, 13, 18, 25, ? समाधान: यहाँ लगातार पदों के बीच का अंतर:

• 10 – 8 = 2
• 13 – 10 = 3
• 18 – 13 = 5
• 25 – 18 = 7

इसलिए, अंतर 2, 3, 5, 7 एक प्राइम नंबर श्रृंखला बनाते हैं। इसलिए अगला अंतर 7 के बाद की अगली प्राइम संख्या होनी चाहिए, जो 11 है।

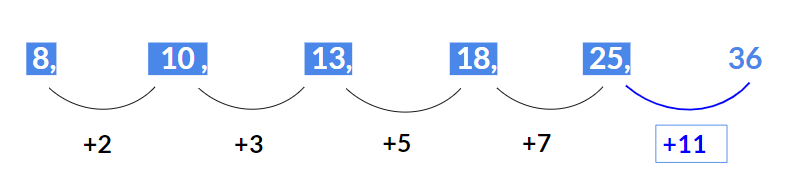
इसलिए, अगला गायब पद होगा 25 + 11 = 36।

(क) सही वर्ग श्रृंखला

एक श्रृंखला जो सही वर्गों पर आधारित होती है और सामान्यतः एक संख्या गायब होती है या गलत स्थान पर होती है।

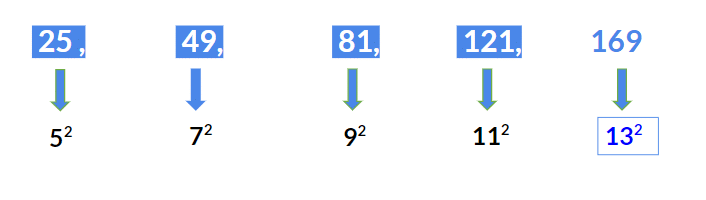
उदाहरण 1: दिए गए श्रृंखला 25, 49, 81, 121, …… का अगला पद खोजें। हल: उपरोक्त श्रृंखला 5 से शुरू होने वाले लगातार विषम संख्याओं के सही वर्गों की श्रृंखला है अर्थात:

• 25 = 5²
• 49 = 7²
• 81 = 9²
• 121 = 11²

इसलिए अगला पद 13² = 169 होगा।

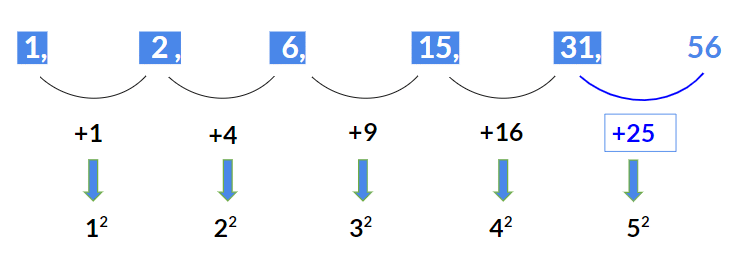
उदाहरण 2: दिए गए श्रृंखला 1, 2, 6, 15, 31…….. में अगला पद खोजें। हल: यहाँ लगातार पदों के बीच का अंतर है:

• 2 – 1 = 1
• 6 – 2 = 4
• 15 – 6 = 9
• 31 – 15 = 16

हम देखते हैं कि अंतर 1, 4, 9, 16 सही वर्ग हैं।

इसलिए अगला पद 31 + 25 = 31 + 52 = 56 होना चाहिए।

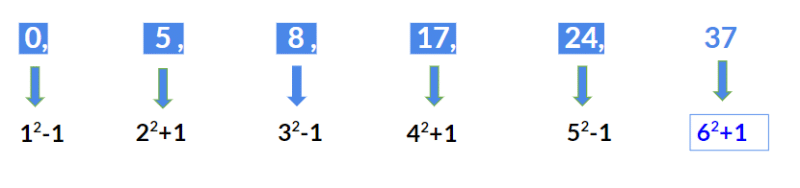
उदाहरण 3: 0, 5, 8, 17, 24, ? हल: उपरोक्त श्रृंखला में, जो पैटर्न पालन किया जा रहा है वह नीचे दिया गया है:

• पहला पद 0 = 1² – 1
• दूसरा पद 5 = 2² + 1
• तीसरा पद 8 = 3² – 1
• चौथा पद 17 = 4² + 1
• पांचवां पद 24 = 5² – 1

हम देखते हैं कि श्रृंखला वैकल्पिक रूप से [(प्राइम)2 – 1] और [(प्राइम)2 + 1] है।

इसलिए अगला पद 6² + 1 = 37 होना चाहिए।

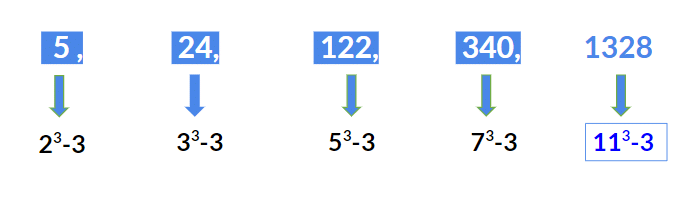
(ख) सही घन श्रृंखला

यह श्रृंखला एक विशेष क्रम में सही घनों पर आधारित होती है और सामान्यतः एक संख्या गायब होती है या गलत स्थान पर होती है।

अध्याय नोट्स

अध्याय में संख्याओं की श्रृंखलाओं के विभिन्न प्रकारों पर चर्चा की गई है। ये श्रृंखलाएँ गणित के महत्वपूर्ण भाग हैं। नीचे कुछ उदाहरण और उनके समाधान दिए गए हैं:

1. पूर्ण घन श्रृंखला:

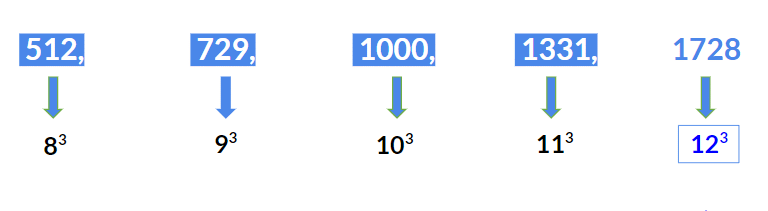
उदाहरण 1: अगली संख्या खोजें 512, 729, 1000, 1331, ?

• पहली संख्या 512 = 8³
• दूसरी संख्या 729 = 9³
• तीसरी संख्या 1000 = 10³
• चौथी संख्या 1331 = 11³

इसलिए अगली संख्या 12³ = 1728 होगी।

2. अंकगणितीय श्रृंखला:

यह एक श्रृंखला है जिसमें अगली संख्या पिछले संख्या में एक निश्चित संख्या जोड़कर या घटाकर प्राप्त की जाती है।

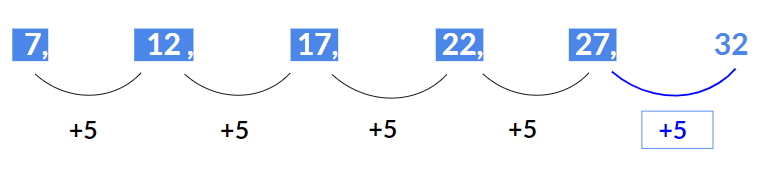
उदाहरण 1: अगली संख्या खोजें 7, 12, 17, 22, 27, ?

यह श्रृंखला एक अंकगणितीय श्रृंखला है जहां प्रत्येक संख्या में 5 जोड़ा जाता है।

• 12 = 7 + 5
• 17 = 12 + 5
• 22 = 17 + 5
• 27 = 22 + 5

इसलिए अगली संख्या 27 + 5 = 32 होगी।

उदाहरण 2: गायब संख्या लिखें 29, 23, 17, 11, ?

यह श्रृंखला एक अंकगणितीय श्रृंखला है जहां प्रत्येक संख्या से 6 घटाया जाता है।

• 29 – 6 = 23
• 23 – 6 = 17
• 17 – 6 = 11

इसलिए अगली संख्या 11 - 6 = 5 होगी।

3. ज्यामितीय श्रृंखला:

यह एक श्रृंखला है जहाँ प्रत्येक अगली संख्या को पिछले संख्या को एक निश्चित संख्या से गुणा या विभाजित करके प्राप्त किया जाता है।

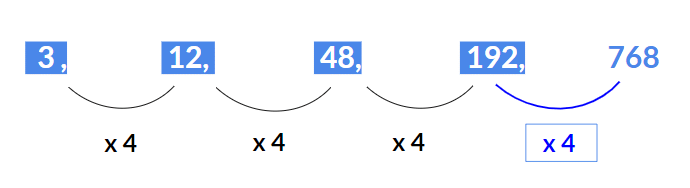
उदाहरण 1: गायब संख्या खोजें 3, 12, 48, 192, ?

यहाँ प्रत्येक संख्या को 4 से गुणा किया जाता है।

12 = 3 x 448 = 12 x 4192 = 48 x 4

• इसलिए अगला पद होगा 192 x 4 = 768.

उदाहरण 2: अगले पद को खोजें 729, 243, 81, 27, ? समाधान: यहाँ प्रत्येक संख्या को 3 से विभाजित किया गया है ताकि अगली संख्या प्राप्त की जा सके.

• 729/3 = 243
• 243/3 = 81
• 81/3 = 27

इसलिए अगला पद होगा 27/3 = 9.

(f) मिश्रित श्रृंखला A series where more than one pattern is arranged in a single series.

उदाहरण 1: लापता पद को खोजें 2, 8, 26, 80, 242, ? समाधान: यहाँ पैटर्न है (x 3 2).

• 2 x 3 2 = 8
• 8 x 3 2 = 26
• 26 x 3 2 = 80
• 80 x 3 2 = 242

इसलिए लापता पद होगा 242 x 3 2 = 728

उदाहरण 2: अगले पद को खोजें 5, 12, 27, 59, ? समाधान: यहाँ प्रत्येक पद को 2 से गुणा किया जाता है और लगातार prime numbers जोड़े जाते हैं.

• 5 x 2 + 2 = 12
• 12 x 2 + 3 = 27
• 27 x 2 + 5 = 59

इसलिए अगला पद होगा 59 x 2 + 7 = 125.

(g) अंकगणितीय – ज्यामितीय श्रृंखला

एक श्रृंखला जो अंकगणितीय और ज्यामितीय श्रृंखला का संयोजन है.

उदाहरण: अगले पद को खोजें 3, 5, 10, 12, 24, 26, ? समाधान: यहाँ पैटर्न है ( 2, x 2, 2, x 2 …..)

• 3 + 2 = 5
• 5 x 2 = 10
• 10 + 2 = 12
• 12 x 2 = 24
• 24 + 2 = 26

इसलिए अगला पद होगा 26 x 2 = 52.

(h) वैकल्पिक श्रृंखला

एक श्रृंखला जहाँ दो श्रृंखलाएँ एकल श्रृंखला में संयोजित होती हैं.

उदाहरण 1: अगले पद को खोजें 2, 3, 5, 8, 8, 13, 11, ? समाधान: यहाँ वैकल्पिक पद जो 2 से शुरू होते हैं, एक अंकगणितीय श्रृंखला बनाते हैं जिसमें सामान्य अंतर 3 है. (2, 5, 8, 11) ► इसके अलावा, वैकल्पिक पद जो 3 से शुरू होते हैं, एक अन्य अंकगणितीय श्रृंखला बनाते हैं जिसमें सामान्य अंतर 5 है. (3, 8, 13,..)

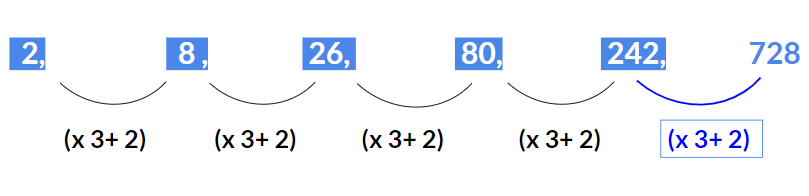
अतः अगला पद 18 होगा।

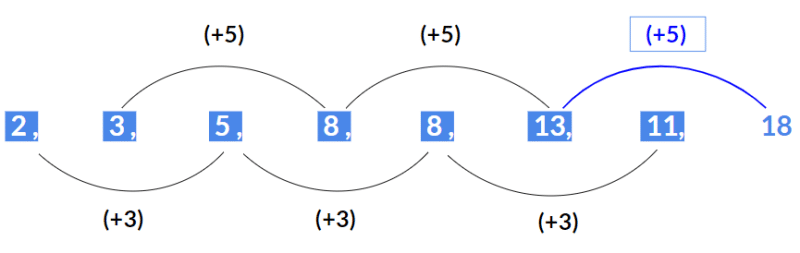
उदाहरण 2: अगला पद खोजें 3, 5, 7, 10, 11, 15, 15, ? समाधान: यहां वैकल्पिक पद, जो 3 से शुरू होते हैं, एक गणितीय श्रेणी बनाते हैं जिसमें सामान्य अंतर 4 है। (3, 7, 11, 15) साथ ही, 5 से शुरू होने वाले वैकल्पिक पद एक ज्यामितीय श्रेणी बनाते हैं जिसमें सामान्य अनुपात 2 है। (5, 10, 15) अतः अगला पद 20 होगा।

किसी भी MBA प्रवेश परीक्षा में, संख्या श्रृंखलाओं पर प्रश्नों को तीन प्रकारों में वर्गीकृत किया जा सकता है, जो नीचे चर्चा की गई हैं:

➢ प्रकार 1: एक संख्या श्रृंखला जिसमें एक विशेष संख्या गायब है। इसलिए, हमें गायब पद या अगला पद खोजना है।

उदाहरण 1: अगला पद खोजें 4, 6, 9, 13, 18, ? समाधान: यहां जो पैटर्न अनुसरण किया जा रहा है वह है (2, 3, 4, 5 आदि)

• 4 + 2 = 6
• 6 + 3 = 9
• 9 + 4 = 13
• 13 + 5 = 18

अतः अगला पद 18 + 6 = 24 होगा।

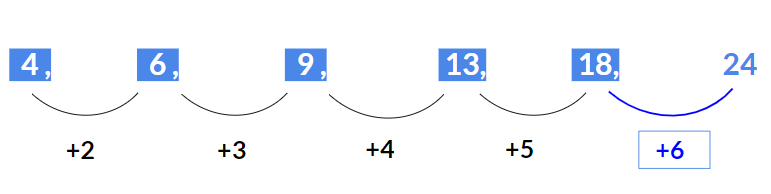
उदाहरण 2: गायब पद खोजें 8, 24, 12, ?, 18, 54 समाधान: यहां पैटर्न है (x 3 ; ÷ 2, x 3, ÷ 2 आदि)

• 8 x 3 = 24
• 24 ÷ 2 = 12
• 12 x 3 = 36
• 36 ÷ 2 = 18
• 18 x 3 = 54

अतः गायब पद 12 x 3 = 36 होगा।

➢ प्रकार 2

एक संख्या श्रृंखला जिसमें एक संख्या गलत स्थान पर है।

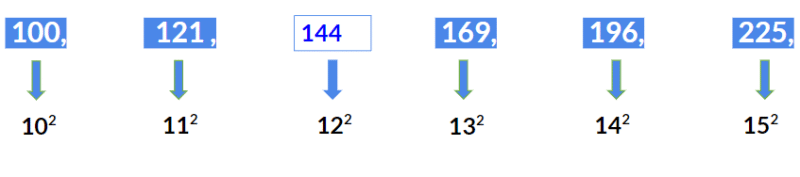
उदाहरण 1: गलत पद खोजें 100, 121, 143, 169, 196, 225। समाधान: उपरोक्त श्रृंखला एक पूर्णांक वर्ग श्रृंखला है जो 10 से शुरू होती है।

• 10² = 100
• 11² = 121
• 12² = 144
• 13² = 169
• 14² = 196
• 15² = 225

अतः 143 गलत स्थान पर है। इसके बजाय यह 12² = 144 होना चाहिए।

उदाहरण 2: गलत पद खोजें 2, 2, 4, 12, 50, 240 समाधान: उपरोक्त श्रृंखला में जो पैटर्न अनुसरण किया जा रहा है वह है (x1, x2, x3, x4, x5)।

• 2 x 1 = 2
• 2 x 2 = 4
• 2 x 3 = 6
• 2 x 4 = 8
• 2 x 5 = 10

इसलिए गलत जगह पर रखा गया नंबर 50 है। इसके बजाय यह 12 x 4 = 48 होना चाहिए।

➢ प्रकार 3

➢ प्रकार 3

➢ प्रकार 3

एक पूर्ण संख्यात्मक श्रृंखला दी गई है जिसके बाद एक अधूरी संख्यात्मक श्रृंखला है।

उदाहरण 1: [67, 84, 95] : [?, 133, 144] समाधान: पहले सेट में संख्याएँ [67, 84, 95] हैं: 84 – 67 = 17 95 – 84 = 11 इसलिए दूसरे सेट में भी वही अंतर बनाए रखना आवश्यक है। 116 – 133 = 17 144 – 133 = 11

इसलिए गायब संख्या 116 होनी चाहिए।

उदाहरण 2: [3, 6, 12] : [4, ?, 16] समाधान: पहले सेट में संख्याएँ पिछले नंबर को दोगुना करके प्राप्त की जाती हैं: 3 x 2 = 6 6 x 2 = 12 इसलिए दूसरे सेट में भी वही पैटर्न बनाए रखना आवश्यक है। 4 x 2 = 8 8 x 2 = 16 इसलिए गायब संख्या 4 x 2 = 8 होगी।