Open App

RRB NTPC/ASM/CA/TA Exam > RRB NTPC/ASM/CA/TA Notes > General Awareness & Knowledge for RRB NTPC (Hindi) > सतही तनाव

सतही तनाव | General Awareness & Knowledge for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA PDF Download

सतह तनाव

जब थोड़ी मात्रा में पानी एक साफ कांच की प्लेट पर डाला जाता है, तो यह पतली परत में फैलता है।
पारा (Mercury) जब कांच की प्लेट पर डाला जाता है, तो यह फैलने के बजाय गोल बूँद बनाता है।
चिकनी कांच की प्लेट पर पानी, पारे की तरह छोटे-छोटे बूँदों में बदल जाता है।
यह व्यवहार दिखाता है कि गुरुत्वाकर्षण के अलावा, एक और बल है जो तरल पदार्थों के आकार को प्रभावित करता है, जो वे जिस सतह को छूते हैं।
जब तरल बहुत हल्का होता है, तो यह बारिश की बूँदों या साबुन के बुलबुले की तरह एक आदर्श गेंद के आकार में बन जाता है।
एक निश्चित मात्रा के तरल के लिए, एक गोला का सबसे छोटा सतह क्षेत्र होता है।
तरल पदार्थ सतह तनाव के कारण अपने सतह क्षेत्र को न्यूनतम करने की प्रवृत्ति रखते हैं।

सतह तनाव की परिभाषा

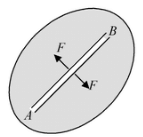
सतही तनाव | General Awareness & Knowledge for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA

कल्पना कीजिए कि एक तरल सतह पर एक काल्पनिक रेखा AB है। इस रेखा के दोनों ओर की सतह दूसरी ओर पर खींचने वाला बल लगाती है, जो सतह के तल में होती है और AB पर लंबवत होती है। तरल का सतह तनाव रेखा AB की एकाई लंबाई पर बल के द्वारा मापा जाता है। यदि F रेखा AB की लंबाई l के दोनों ओर कुल बल है, तो सतह तनाव T को T=F/l के रूप में दिया जाता है। इस प्रकार, सतह तनाव को उस काल्पनिक रेखा पर सतह के तल में लंबवत कार्यरत बल के एकाई लंबाई के रूप में परिभाषित किया जाता है। इसकी इकाई न्यूटन/मीटर है, जिसमें आयाम [MT-2] होते हैं।

सतह तनाव का मान तरल के तापमान और सतह के दूसरी ओर के माध्यम पर निर्भर करता है। यह तापमान बढ़ने पर घटता है और критिकल तापमान पर शून्य हो जाता है।

सतह ऊर्जा

एक तरल के सतह क्षेत्र को बढ़ाने के लिए अणुओं के बीच आकर्षण बल के खिलाफ कार्य की आवश्यकता होती है, जो नए सतह में संभावित ऊर्जा के रूप में संग्रहीत होती है। इसके अलावा, सतह क्षेत्र के बढ़ने के कारण ठंडा होना होता है, इसलिए स्थिर तापमान बनाए रखने के लिए आस-पास से गर्मी जोड़ी जाती है। सतह के क्षेत्र के प्रति एकाई इस अतिरिक्त ऊर्जा को सतह ऊर्जा कहा जाता है।

सतह तनाव और सतह क्षेत्र बढ़ाने में किए गए कार्य के बीच संबंध

एक मुड़ी हुई तार ABC और एक सीधी, चलने योग्य तार PQ के बीच एक तरल फिल्म पर विचार करें। जैसे ही फिल्म संकुचन की प्रवृत्ति करती है, PQ ऊपर की ओर बढ़ता है, जिससे इसे संतुलन में बनाए रखने के लिए नीचे की ओर एक बल F की आवश्यकता होती है। F, PQ के साथ संपर्क में फिल्म की लंबाई l के सीधे अनुपात में है। चूंकि दो स्वतंत्र सतहें हैं, इसलिए F∝2l या F=T×2l, जहाँ T सतह तनाव है।

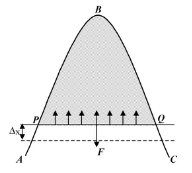
यदि PQ को एक छोटे दूरी Δx द्वारा नीचे की ओर ले जाया जाता है, जिससे फिल्म का सतह क्षेत्र बढ़ता है, तो बल F द्वारा किया गया कार्य W = F × Δx = T × 2l × Δx है। चूंकि 2l × Δx कुल क्षेत्र में वृद्धि (ΔA) है, इसलिए W = T × ΔA। इस प्रकार, सतह तनाव T उस कार्य के बराबर है जो तरल फिल्म के सतह क्षेत्र को एकता से बढ़ाने के लिए आवश्यक है, जिसे स्थिर तापमान पर जूल प्रति वर्ग मीटर में व्यक्त किया जाता है।

एक बूँद के अंदर अतिरिक्त दबाव

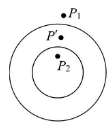
हम एक गोलाकार तरल बूँद पर विचार करते हैं जिसका त्रिज्या R है। यदि बूँद छोटी है, तो गुरुत्वाकर्षण का प्रभाव नजरअंदाज किया जा सकता है और आकृति गोलाकार मानी जा सकती है। यदि सतह के ठीक बाहर दबाव P1 है और सतह के ठीक अंदर दबाव P2 है। तो P2 - P1 = 2T/R। सतह के अंदर का दबाव सतह के बाहर के दबाव से अधिक है।

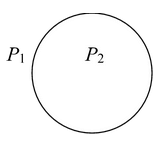
नोट: अवतल पक्ष पर दबाव उत्तल पक्ष पर दबाव से अधिक है। यदि तरल के अंदर एक वायु बुलबुला है जैसा कि चित्र में दिखाया गया है, तो एकल सतह का निर्माण होता है। अवतल पक्ष पर वायु है और उत्तल पक्ष पर तरल है। अवतल पक्ष का दबाव उत्तल पक्ष के दबाव से 2T/R द्वारा अधिक है। P2 - P1 = 2T/R

साबुन के बुलबुले के भीतर अत्यधिक दबाव

मान लें कि बुलबुले के बाहर का वायु दबाव P1 है, साबुन के घोल के भीतर P′ है और बुलबुले के भीतर वायु का दबाव P2 है।

P′ - P1 = 2T/R इसी तरह, आंतरिक सतह को देखते हुए, P2 - P′ = 2T/R। इन दोनों समीकरणों को जोड़ने पर, P2 - P1 = 4T/R।

संपर्क का कोण

ठोस सतह पर स्पर्श बिंदु पर ठोस सतह के टेंजेंट और तरल सतह के टेंजेंट के बीच का कोण संपर्क का कोण कहलाता है। उन तरल पदार्थों के लिए जो ठोस को भिगोते हैं, कोण तीव्र होता है; और जो नहीं भिगोते, उनका कोण obtuse होता है। उदाहरण के लिए, शुद्ध पानी और साफ कांच का संपर्क कोण शून्य होता है, सामान्य पानी और कांच का लगभग 8°, और पारा और कांच का 135° होता है। पानी और चांदी के लिए यह 90° होता है, जब पानी की सतह चांदी के बर्तन में क्षैतिज होती है।

कैपिलैरिटी

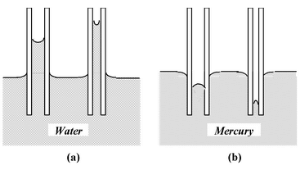
जब एक कांच की कैपिलरी ट्यूब, जो दोनों अंत में खुली होती है, पानी में ऊर्ध्वाधर रखी जाती है, तो पानी ट्यूब में बाहर के पानी के स्तर से एक विशेष ऊँचाई तक चढ़ता है। ट्यूब जितनी संकीर्ण होती है, पानी उतनी ही ऊँचाई पर चढ़ता है। इसके विपरीत, जब ट्यूब को पारे में रखा जाता है, तो पारा बाहर के स्तर से नीचे धकेल दिया जाता है। कैपिलरी ट्यूब में तरल पदार्थों के उठने या गिरने की घटना को कैपिलैरिटी कहा जाता है।
जो तरल कांच पर चिपकते हैं (जहां संपर्क का कोण तीव्र होता है) वे कैपिलरी ट्यूब में ऊपर की ओर बढ़ते हैं, जबकि जो कांच पर चिपकते नहीं हैं (जहां संपर्क का कोण चौड़ा होता है) वे कैपिलरी में नीचे की ओर बढ़ते हैं।

व्याख्या:

कैपिलैरिटी की घटना तरल पदार्थों की सतही तनाव के कारण उत्पन्न होती है। जब एक कैपिलरी ट्यूब को पानी में डुबाया जाता है, तो ट्यूब के भीतर पानी का मेनिस्कस आंतरिक रूप से अवतल होता है। मेनिस्कस के ठीक नीचे का दबाव मेनिस्कस के ठीक ऊपर के दबाव से 2T/R कम होता है, जहां T पानी की सतही तनाव है और R मेनिस्कस की वक्रता का व्यास है।

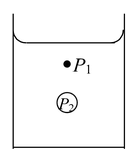
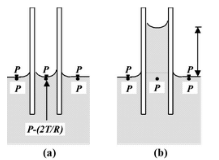
पानी की सतह का दबाव वायुमंडलीय दबाव P है। ट्यूब के बाहर पानी की समतल सतह के ठीक नीचे का दबाव भी P है, लेकिन ट्यूब के अंदर मेनिस्कस के ठीक नीचे का दबाव P - (2T/R) है। हम जानते हैं कि पानी की एक ही स्तर पर सभी बिंदुओं पर दबाव समान होना चाहिए।

इसलिए, मेनिस्कस के नीचे दबाव की कमी 2T/R की भरपाई करने के लिए, पानी बाहर से ट्यूब में बहने लगता है। कैपिलरी में उठने वाली पानी की शक्ति एक निश्चित ऊँचाई h पर रुक जाती है। इस स्थिति में, ऊँचाई h की पानी की स्तंभ का दबाव 2T/R के बराबर हो जाता है, अर्थात्,

hρg = 2T/R

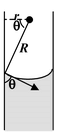
जहाँ ρ पानी का घनत्व है और g गुरुत्वाकर्षण का त्वरण है। यदि r कैपिलरी ट्यूब का व्यास है और θ पानी- कांच का सम्पर्क कोण है, तो मेनिस्कस की वक्रता का व्यास R = r/cosθ है। ∴ hρg = 2T/r/cosθ या h = 2Tcos θ/rρg

यह दिखाता है कि जैसे-जैसे r घटता है, h बढ़ता है, अर्थात्, ट्यूब जितनी संकीर्ण होगी, तरल उतनी ही ऊँचाई तक ट्यूब में उठेगा।

अपर्याप्त लंबाई की कैपिलरी ट्यूब में तरल का उठना: मान लीजिए कि घनत्व ρ और सतही तनाव T वाला तरल एक कैपिलरी ट्यूब में ऊँचाई h तक उठता है। तब hρg = 2T/R जहाँ R ट्यूब में तरल मेनिस्कस की वक्रता का व्यास है। इससे हम लिख सकते हैं hR = 2T/ρg = constant (किसी दिए गए तरल के लिए)

जब ट्यूब की लंबाई h से अधिक होती है, तो तरल ट्यूब में ऐसी ऊँचाई तक उठता है ताकि उपरोक्त संबंध को संतोषजनक बना सके। लेकिन यदि ट्यूब की लंबाई h से कम हो, मान लीजिए h′, तो तरल ट्यूब के शीर्ष तक उठता है और फिर फैलता है जब तक कि इसकी वक्रता R बढ़कर R′ नहीं हो जाती, इस प्रकार h′R′ = hR = 2T/ρg। यह स्पष्ट है कि तरल एक छोटे कैपिलरी ट्यूब के ऊपरी सिरे से फव्वारे के रूप में बाहर नहीं आ सकता।

The document सतही तनाव | General Awareness & Knowledge for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA is a part of the RRB NTPC/ASM/CA/TA Course General Awareness & Knowledge for RRB NTPC (Hindi).

All you need of RRB NTPC/ASM/CA/TA at this link: RRB NTPC/ASM/CA/TA

	General Awareness & Knowledge for RRB NTPC (Hindi) 464 docs\|420 tests

General Awareness & Knowledge for RRB NTPC (Hindi)

464 docs|420 tests

Join Course for Free

About this Document

Oct 19, 2025 Last updated

Related Exams

RRB NTPC/ASM/CA/TA Police SI Exams SSC CGL

Document Description: सतही तनाव for RRB NTPC/ASM/CA/TA 2025 is part of General Awareness & Knowledge for RRB NTPC (Hindi) preparation. The notes and questions for सतही तनाव have been prepared according to the RRB NTPC/ASM/CA/TA exam syllabus. Information about सतही तनाव covers topics like and सतही तनाव Example, for RRB NTPC/ASM/CA/TA 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for सतही तनाव.

Introduction of सतही तनाव in English is available as part of our General Awareness & Knowledge for RRB NTPC (Hindi) for RRB NTPC/ASM/CA/TA & सतही तनाव in Hindi for General Awareness & Knowledge for RRB NTPC (Hindi) course. Download more important topics related with notes, lectures and mock test series for RRB NTPC/ASM/CA/TA Exam by signing up for free. RRB NTPC/ASM/CA/TA: सतही तनाव | General Awareness & Knowledge for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA

Description

Full syllabus notes, lecture & questions for सतही तनाव | General Awareness & Knowledge for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA - RRB NTPC/ASM/CA/TA | Plus excerises question with solution to help you revise complete syllabus for General Awareness & Knowledge for RRB NTPC (Hindi) | Best notes, free PDF download

Information about सतही तनाव

In this doc you can find the meaning of सतही तनाव defined & explained in the simplest way possible. Besides explaining types of सतही तनाव theory, EduRev gives you an ample number of questions to practice सतही तनाव tests, examples and also practice RRB NTPC/ASM/CA/TA tests

	General Awareness & Knowledge for RRB NTPC (Hindi) 464 docs\|420 tests

General Awareness & Knowledge for RRB NTPC (Hindi)

464 docs|420 tests

Join Course for Free

Download as PDF

Explore Courses for RRB NTPC/ASM/CA/TA exam

सतही तनाव | General Awareness & Knowledge for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA

Sample Paper

practice quizzes

mock tests for examination

Semester Notes

past year papers

study material

Viva Questions

ppt

Previous Year Questions with Solutions

Extra Questions

video lectures

pdf

shortcuts and tricks

Important questions

Summary

Exam

MCQs

Objective type Questions

Free

सतही तनाव | General Awareness & Knowledge for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA

;

Additional Information about सतही तनाव for RRB NTPC/ASM/CA/TA Preparation

सतही तनाव Free PDF Download

The सतही तनाव is an invaluable resource that delves deep into the core of the RRB NTPC/ASM/CA/TA exam. These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective. With the help of these notes, you can grasp complex subjects quickly, revise important points easily, and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner, allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material, or toppers' notes, this PDF has got you covered. Download the सतही तनाव now and kickstart your journey towards success in the RRB NTPC/ASM/CA/TA exam.

Importance of सतही तनाव

The importance of सतही तनाव cannot be overstated, especially for RRB NTPC/ASM/CA/TA aspirants. This document holds the key to success in the RRB NTPC/ASM/CA/TA exam. It offers a detailed understanding of the concept, providing invaluable insights into the topic. By knowing the concepts well in advance, students can plan their preparation effectively. Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.

सतही तनाव Notes

सतही तनाव Notes offer in-depth insights into the specific topic to help you master it with ease. This comprehensive document covers all aspects related to सतही तनाव. It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation. Practice papers and question papers enable you to assess your progress effectively. Additionally, the paper analysis provides valuable tips for tackling the exam strategically. Access to Toppers' notes gives you an edge in understanding complex concepts. Whether you're a beginner or aiming for advanced proficiency, सतही तनाव Notes on EduRev are your ultimate resource for success.

सतही तनाव RRB NTPC/ASM/CA/TA Questions

The "सतही तनाव RRB NTPC/ASM/CA/TA Questions" guide is a valuable resource for all aspiring students preparing for the RRB NTPC/ASM/CA/TA exam. It focuses on providing a wide range of practice questions to help students gauge their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation. The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level. Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.

Study सतही तनाव on the App

Students of RRB NTPC/ASM/CA/TA can study सतही तनाव alongwith tests & analysis from the EduRev app, which will help them while preparing for their exam. Apart from the सतही तनाव, students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc. The EduRev App will make your learning easier as you can access it from anywhere you want. The content of सतही तनाव is prepared as per the latest RRB NTPC/ASM/CA/TA syllabus.

Education Revolution