Origins of Deviation from Ideal Gas Behaviour | Additional Documents & Tests for Civil Engineering (CE) PDF Download
Origins of Deviation from Ideal Gas Behaviour
The ideal gas EOS is given by eqn. 1.12. While this is a relationship between the macroscopic intensive properties there are two assumptions about the microscopic behaviour of molecules in an ideal gas state:
i. The molecules have no extension in space (i.e., they posses zero volume)
ii. The molecules do not interact with each other
In particular, the second assumption is relatively more fundamental to explaining deviations from ideal gas behavior; and indeed for understanding thermodynamic behavior of real fluids (pure or mixtures) in general. For this, one needs to understand the interaction forces that exist between molecules of any substance, typically at very short intermolecular separation distances (~ 5 – 20A0 (where 1A0 = 10-8m).
Uncharged molecules may either be polar or non-polar depending on both on their geometry as well as the electro-negativity of the constituent atoms. If the centre of total positive and negative charges in a molecule do not coincide (for example, for water), it results in a permanent dipole, which imparts a polarity to the molecule. Conversely, molecules for which the centres of positive and negative charge coincide (for example, methane) do not possess a permanent dipole and are termed non-polar. However, even a so-called non-polar molecule, may possess an instantaneous dipole for the following reason. At the atomic level as electrons oscillate about the positively charged central nucleus, at any point of time a dipole is set up. However, averaged over time, the net dipole moment is zero.
When two polar molecules approach each other closely the electric fields of the dipoles overlap, resulting in their re-orientation in space such that there is a net attractive force between them. If on the other hand a polar molecule approaches a non-polar molecule, the former induces a dipole in the latter (due to displacement of the electrons from their normal position) resulting once again in a net attractive interaction between them. Lastly when two non-polar molecules are close enough their instantaneous dipoles interact resulting in an attractive force. Due to these three types of interactions (dipole-dipole, dipole-induced dipole, and induced dipole-induced dipole) molecules of any substance or a mixture are subjected to an attractive force as they approach each other to very short separation distances.
However, intermolecular interactions are not only attractive. When molecules approach to distances even less than ~ 5 A0 or so, a repulsive interaction force comes into play due to overlap of the electron clouds of each molecule, which results in a repulsive force field between them. Thus if one combines both the attractive and repulsive intermolecular interactions the overall interaction potential U resembles the schematic shown in fig. 2.5.
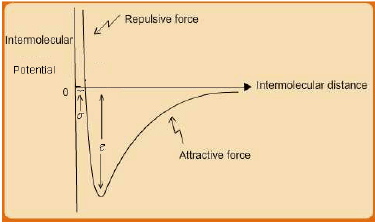
Fig. 2.5 Schematic of Intermolecular potential energy U for a pair of uncharged molecules
Many expressions have been proposed for the overall interaction potential U [see, J.M. Prausnitz, R.N Lichtenthaler and E.G. Azevedo, Molecular Thermodynamics of Fluid Phase Equilibria, (3rd ed.), 1999, Prentice Hall, NJ (USA)]. These are essentially empirical, although their functional forms often are based on fundamental molecular theory of matter. The most widely used equation in this genre is the Lennard-Jones (LJ) 12/6 pair-potential function which is given by eqn. 2.1:
Where, r = intermolecular separation distance; ε, σ = characteristic L-J parameters for a substance.
The r −12 term represents the repulsive interaction, whereas the r−6 term corresponds to the attractive interaction potential. As already indicated, the domain of intermolecular interactions is limited to relatively low range of separation distances. In principle they are expected to be operative over r = 0 −∞; but for practical purposes they reduce to insignificant magnitudes for separations exceeding about 10 times the molecular diameter.
The L-J parameters ε, σ are representative of the molecular interaction and size respectively. Typical values of the L-J equation parameters for various substances may be found elsewhere (G. Maitland, M. Rigby and W. Wakeham, 1981, Intermolecular Forces: Their Origin and Determination, Oxford, Oxford University Press.)
Since gases behave ideally at low pressures, intermolecular separation distances therein are typically much higher than the range over which intermolecular interactions are significant. This is the reason why such interactions are negligible in case of ideal gas, which essentially is one of the assumptions behind the definition of ideal gas state. Indeed while the ideal gas EOS is expressed in macroscopic terms in eqn. 1.12, the same equation may be derived from microscopic (thermodynamic) theory of matter.
The root of non-ideal gas behavior, which typically obtains at higher pressure, thus is due to the fact that at elevated pressures, the intermolecular separations tend to lie within the interactive range and hence the ideal gas assumption is no longer valid. Thus, the ideal gas EOS is insufficient to describe the phase behavior of gases under such conditions.
Intermolecular interactions also help explain the behavior of fluids in other states. Gases can condense when compressed, as molecules are then brought within the separations where the attractive forces constrain the molecules to remain within distances typical of liquid phase. It follows that a pure component liquid phase cannot be ideal in the same sense as a gas phase can be. Further, the fact that liquids are far less compressible also is due to the repulsive forces that operate at close intermolecular distances. Obviously these phenomena would not be observed unless there were interactions between molecules. Thus, it follows that while properties of the ideal gas depend only on those of isolated, non-interacting moleclues, those of real fluids depends additionally on the intermolecular potential. Properties which are determined by the intermolecular interaction are known as configurational properties, an example of which is the energy required for vapourization; this is because during the process of vapourization energy has to be provided so as to overcome the intermolecular attractive force between molecules in the liquid phase and achieve the gas state where the seprations are relatively larger.
FAQs on Origins of Deviation from Ideal Gas Behaviour - Additional Documents & Tests for Civil Engineering (CE)
| 1. What is ideal gas behaviour and why is it important in civil engineering? |  |
| 2. What factors can cause deviation from ideal gas behavior in civil engineering applications? |  |
| 3. How can the deviation from ideal gas behavior be quantified in civil engineering calculations? |  |
| 4. What are some common applications of understanding deviation from ideal gas behavior in civil engineering? |  |
| 5. How can engineers account for deviation from ideal gas behavior in civil engineering design and analysis? |  |





















