Problem Solving on DC Machines | Basic Electrical Technology - Electrical Engineering (EE) PDF Download
| Table of contents |

|
| Introduction |

|
| Shunt Motor Problems |

|
| Problems on Series Motor |

|
| D.C Generator Problems |

|
Introduction
In this lecture, some typical problems on D.C machines are worked out not only to solve the problems but also to bring out important features of the motors involving its performance. To begin with, few problems on d.c motors have been solved and then problems on the generator are taken up. 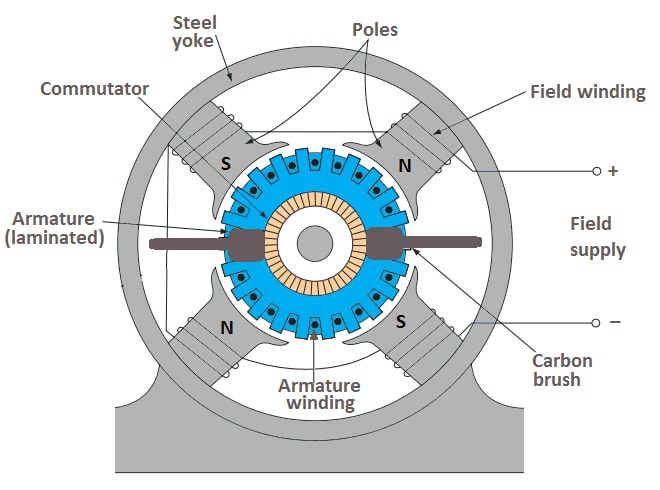 D.C MotorFor a beginner, it is suggested to follow the following guidelines for successful completion of the problem.
D.C MotorFor a beginner, it is suggested to follow the following guidelines for successful completion of the problem.
- Read the problem and note down the information provided about the motor.
- In general, some initial steady operating conditions are given in terms of armature current, field current, speed etc.
- Draw a circuit diagram showing the initial variable values.
- Write down the back emf equation and the torque equation for the initial operating point, it is reiterated here that these two equations hold the key for the gateway of the correct solution.
- In the statement of the problem, with respect to the initial operating point, some variables (like armature resistance, field resistance, load torque, armature applied voltage etc.) will be changed and you will be asked perhaps to calculate new armature current, speed etc.
- Assume the variables to be calculated and write down once again the back emf equation and the torque equation for the new operating point.
- You have now four equations – 2 correspondings to the initial operating point and the other 2 correspondings to the new operating point.
- Take the ratio of the torque equations and the ratio of back emf equations.
- Solve from the above equations the unknown.
Shunt Motor Problems
Q.1. A 220 V shunt motor has armature and field resistance of 0.2 Ω and 220 Ω respectively. The motor is driving a constant load torque and running at 1000 rpm drawing 10 A current from the supply. Calculate the new speed and armature current if an external armature resistance of value 5 Ω is inserted in the armature circuit. Neglect armature reaction and saturation.
Solution: The circuit diagram of the shunt motor is:
For initial operating point: IL1 = 10 A, ra = 0.2 Ω and supply voltage V = 220 V.
Field cur rent If1 = 220/220 A = 1A
Armature cur rent Ia1 = 10A – 1A = 9A
Now we write down the expressions for the torque and back emf.
Since field resistance remains unchanged If2 = If1 = 1 A. Let the new steady armature current be Ia2 and the new speed is n2. In this new condition, the torque and back emf equations are
Taking the ratios of Te2 and Te1 we get,
Now taking the ratio EMFs
we get,
It may be noted that for constant load torque the steady-state armature current does not change with change in the value of the armature resistance. Let us consider the next problem whose data are similar to the first problem except for the fact that load torque is a function of speed.
Q.2. A 220 V shunt motor has armature and field resistances of 0.2 Ω and 220 Ω respectively. The motor is driving load torque, TL ∝ n2 and running at 1000 rpm drawing 10 A current from the supply. Calculate the new speed and armature current if an external armature resistance of value 5 Ω is inserted in the armature circuit. Neglect armature reaction and saturation.
Solution: The field current and armature currents corresponding to the initial operating point are
If1 = 1 A and Ia1 = 9 A
Now torque and back emf equations are:
Let the new steady-state armature current be Ia2 and the new speed is n2. In this new condition, the torque and back emf equations are
Taking the ratios of Te2 and Te1 we get,
Taking the ratios of Eb2 and Eb1 we get,
simplification results into the following quadratic equation:
Q.3. Initially, a d.c shunt motor having ra = 0.5 Ω and Rf = 220 Ω is running at 1000 rpm drawing 20 A from 220 V supply. If the field resistance is increased by 5%, calculate the new steady-state armature current and speed of the motor. Assume the load torque to be constant.
Solution: As usual, let us begin the solution by drawing the shunt motor diagram.
For initial operating point: IL1 = 20 A, ra = 0.5 Ω and supply voltage V = 220 V.
Field cur rent If1 = 220/220 A = 1 A
Armature cur rent Ia1 = 20 A – 1 A = 19 A
Now we write down the expressions for the torque and back emf corresponding to the initial condition.
In this problem, the field Resistance is changed and the new value of field resistance is Rf2 = 1.05 × 220 = 231 Ω. So new field current is If2 = 222/301 = 0.95 A. Let the new steady-state armature current be Ia2 and the new speed is n2. Since load torque remains constant, we have:
To calculate the new speed n2, we have to calculate the new back emf:
Problems on Series Motor
The steps to solve a series motor problem are δ similar to that of solving a shunt motor problem. One has to write down the torque equations and back emf equations corresponding to steady state operating points as before.
However, the following points, which distinguish a series motor from a shunt motor should be carefully noted.
- Field coil being in series with the armature, in general field current If and armature current Ia are same.
- The field coil resistance rse of a series motor is low and is of the order of armature resistance ra.
- The back emf can be calculated as Eb = V – Ia(rse + ra)
- The back emf Eb is also given by: Eb = kφn = k gIfn if saturation is neglected. = k gIan
- Torque developed by the motor is given by: Te = kφIa = k ′If Ia if saturation is neglected. KtIa2
- One should be careful for situations when field current and armature current may not be same. One such situation occurs when a diverter resistance is connected across the field coil for controlling speed.
Q.1. A 220 V d.c series motor has armature and field resistances of 0.15 Ω and 0.10 Ω respectively. It takes a current of 30 A from the supply while running at 1000 rpm. If an external resistance of 1 Ω is inserted in series with the motor, calculate the new steady-state armature current and the speed. Assume the load torque remains constant.
Solution: The problem has first been be pictured in the following figure 41.3.
Figure 41.3:
Since the load torque remains constant in both the cases, we have:
Now equations involving back emfs:
In the second case:
Thus taking the ratio of Eb2 and Eb1 we get:
Q.2. A 220 V d.c series motor has armature and field resistances of 0.15 Ω and 0.10 Ω respectively. It takes a current of 30 A from the supply while running at 1000 rpm. If an external resistance of 1 Ω is inserted in series with the motor, calculate the new steady state armature current and the speed. Assume the load torque is proportional to the square of the speed i.e., TL ∝ n2.
Solution: This problem is same as the first one except for the fact load torque is not constant but proportional to the square of the speed. Thus:
Ratio of back emfs give:
Next let us solve a problem when a diverter resistance is connected across the field coil.
Q.3. A 220 V d.c series motor has armature and field resistances of 0.15 Ω and 0.10 Ω respectively. It takes a current of 30 A from the supply while running at 1000 rpm. If a diverter resistance of 0.2 Ω is connected across the field coil of the motor, calculate the new steady state armature current and the speed. Assume the load torque remains constant.
Solution: Following figure 41.4 shows the 2 cases in which the motor operate.
Figure 41.4:
In the second case it may be noted that If2 ≠ Ia2. In fact, If2 is a fraction of Ia2. Since the field coil and diverter are connected in parallel we have:
Since load torque remains constant, we have:
Now we calculate the back emfs:
In the second case:
Thus taking the ratio of Eb2 and Eb1 we get:
D.C Generator Problems
Q.1. The following data refer to the O.C.C of a D.C separately excited generator at 1000 rpm. 
The machine is now connected as a shunt generator with a total field resistance of 200 Ω and driven at 1000 rpm. Estimate graphically: (i) the voltage to which the generator will build up at no load. (ii) the armature, field and load currents when the terminal voltage is found to be 150 V. Neglect the effect of armature reaction and brush drop and assume armature resistance ra to be 0.8 Ω. (iii) Finally estimate the steady state armature current when the machine terminals are shorted.
Solution: First of all the OCC of the generator is plotted in a graph paper as shown in figure 41.5.
(i) The total field circuit resistance is given to be Rf = 200 Ω. The Rf line is now drawn on the same graph paper passing through the origin. The point of intersection of the Rf line and the OCC decides the final no load voltage and can be read from the graph as 192 V and the corresponding field current is 0.96 A.
(ii) Since the terminal voltage V is 150 V(= BM), field current If is OM = 0.77 A. Generated voltage E is given by AM. But we know E = Iara + V. Hence Iara = E – V = AM – BM = AB. Now from the graph AB = 25 V. ∴Ia = 25/0.8 = 31.25 A. So load current IL = Ia – If = 31.25 – 0.77 = 30.48 A. Various currents are shown in the circuit diagram (figure 41.6).
Operation of D.C. Machine Connected to D.C. Bus (Fixed D.C. Voltage)
- Generally, a d.c machine connected to a fixed voltage source is expected to operate as a motor drawing current from the source as shown in figure 41.7 (a).
- However, the same machine may operate as a generator as well as feeding power to the d.c bus as shown in figure 41.7 (b). That it will act as a motor or generator is decided by the fact whether the generated emf E of the machine is less than or more than the supply voltage V.
- In figure 41.7 (a), E < V so armature will draw current given by Ia = (V – E)/ra and the machine acts as a motor.
- However by some means, if E could be made greater than the supply voltage V, the direction of armature current will be reversed and its value is given by Ia = (E – V)/ra i.e., a current IL = Ia – If will be fed to the supply and the machine will act as a generator.
- Of course to achieve this, one has to remove the mechanical load from the shaft and run it at a higher speed with a prime mover to ensure E > V.
- Remember E being equal to kg If n and If held constant, one has to increase speed so as to make E more than V.
The following problem explains the above operation:
Q.2. A 200 V, d.c shunt machine has an armature resistance of 0.5 Ω and field resistance of 200 Ω. The machine is running at 1000 rpm as a motor drawing 31 A from the supply mains. Calculate the speed at which the machine must be driven to achieve this as a generator.
Solution: First draw the circuit diagrams showing the motoring and generating mode of operation indicating the currents and their directions as in figure 41.8.
For motor mode:
Current drawn from supply, IL = 31 A
Figure 41.8
Field current, If = 200/200 = 1A
Armature current, Ia1 = 31 – 1 = 30 A
Back emf, Eb = 200 – 30 × 0.5
or, kIf n1 = 185 V
Since speed, n1 = 1 000 rpm
so, k × 1 × 1000 = 185 V
Similarly for generator mode:
Current fed to supply, IL = 31 A
Field current, If = 200/200 = 1A
Armature, Ia2 = 31 + 1 = 3 2 A
Generated emf, Eg = 200 + 32 × 0.5
or, k If n2 = 216V where n2 is the unknown speed
Now taking the ratio of Eg and Eb we get:
|
74 docs|62 tests
|
FAQs on Problem Solving on DC Machines - Basic Electrical Technology - Electrical Engineering (EE)
| 1. What are some common problems with shunt motors? |  |
| 2. What are some problems that can occur with series motors? |  |
| 3. What are some common problems that can occur with DC generators? |  |
| 4. How can I solve problems with DC machines? |  |
| 5. What are some tips for troubleshooting DC machines? |  |
















