Eigenvalues, eigenvectors of tensors
The scalar λi characterize eigenvalues (or principal values) of A if there exist corresponding nonzero normalized eigenvectors 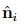 (or principal directions or principal axes) of A, so that
(or principal directions or principal axes) of A, so that
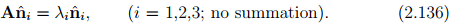
To identify the eigenvectors of a tensor, we use subsequently a hat on the vector quantity concerned, for example, 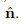 .
.
Thus, a set of homogeneous algebraic equations for the unknown eigenvalues λi , i = 1,2,3, and the unknown eigenvectors 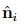 , i = 1,2,3, is
, i = 1,2,3, is
(A − λi1)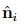 = o, (i = 1,2,3; no summation). (2.137)
= o, (i = 1,2,3; no summation). (2.137)
For the above system to have a solution 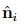 ≠ o the determinant of the system must vanish. Thus,
≠ o the determinant of the system must vanish. Thus,
det(A − λi1) = 0 (2.138)
where
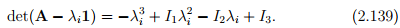
This requires that we solve a cubic equation in λ, usually written as
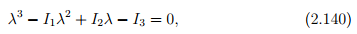
called the characteristic polynomial (or equation) for A, the solutions of which are the eigenvalues λi , i = 1,2,3. Here, Ii , i = 1,2,3, are the so-called principal scalar invariants of A and are given by
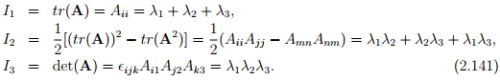
If A is invertible then we can compute I2 using the expression I2 = tr(A−1 ) det(A). A repeated application of tensor A to equation (2.136) yields 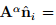
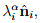 i = 1,2,3, for any positive integer α. (If A is invertible then α can be any integer; not necessarily positive.) Using this relation and (2.140) multiplied by
i = 1,2,3, for any positive integer α. (If A is invertible then α can be any integer; not necessarily positive.) Using this relation and (2.140) multiplied by 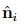 , we obtain the well-known Cayley-Hamilton equation:
, we obtain the well-known Cayley-Hamilton equation:
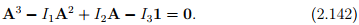
It states that every second order tensor A satisfies its own characteristic equation. As a consequence of Cayley-Hamilton equation, we can express Aα in terms of A2 , A, 1 and principal invariants for positive integer, α > 2. (If A is invertible, the above holds for any integer value of α positive or negative provided α ≠ {0, 1, 2}.)
For a symmetric tensor S the characteristic equation (2.140) always has three real solutions and the set of eigenvectors form a orthonormal basis {nˆi} (the proof of this statement is omitted). Hence, for a positive definite symmetric tensor A, all eigenvalues λi are (real and) positive since, using (2.136), we have λi =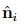 �
� 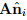 > 0, i = 1,2,3.
> 0, i = 1,2,3.
Any symmetric tensor S may be represented by its eigenvalues λi , i = 1,2,3, and the corresponding eigenvectors of S forming an orthonormal basis {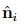 }. Thus, S can be expressed as
}. Thus, S can be expressed as
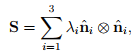 (2.143)
(2.143)
called the spectral representation (or spectral decomposition) of S. Thus, when orthonormal eigenvectors are used as the Cartesian basis to represent S then
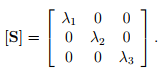 (2.144)
(2.144)
The above holds when all the three eigenvalues are distinct. On the other hand, if there exists a pair of equal roots, i.e., λ1 = λ2 ≠ λ3, with an unique eigenvector 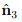 associated with λ3, we deduce that
associated with λ3, we deduce that
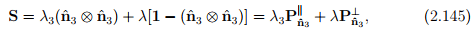
where 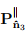 and
and 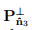 denote projection tensors introduced in (2.109) and (2.110) respectively. Finally, if all the three eigenvalues are equal, i.e., λ1 = λ2 = λ3 = λ, then
denote projection tensors introduced in (2.109) and (2.110) respectively. Finally, if all the three eigenvalues are equal, i.e., λ1 = λ2 = λ3 = λ, then
S = λ1, (2.146)
where every direction is a principal direction and every set of mutually orthogonal basis denotes principal axes.
It is important to recognize that eigenvalues characterize the physical nature of the tensor and that they do not depend on the coordinates chosen.
Square root theorem Let C be symmetric and positive definite tensor. Then there is a unique positive definite, symmetric tensor U such that
U2 = C. (2.147)
We write 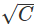 for U. If spectral representation of C is:
for U. If spectral representation of C is:
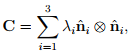 (2.148)
(2.148)
then the spectral representation for U is:
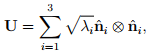 (2.149)
(2.149)
where we have assumed that the eigenvalues of C, λi are distinct. On the other hand if λ1 = λ2 = λ3 = λ then
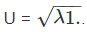 (2.150)
(2.150)
If λ1 = λ2 = λ ≠ λ3, with an unique eigenvector 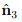 associated with λ3 then
associated with λ3 then
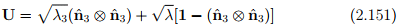
(or principal directions or principal axes) of A, so that
.
, i = 1,2,3, is
= o, (i = 1,2,3; no summation). (2.137)
≠ o the determinant of the system must vanish. Thus,
i = 1,2,3, for any positive integer α. (If A is invertible then α can be any integer; not necessarily positive.) Using this relation and (2.140) multiplied by
, we obtain the well-known Cayley-Hamilton equation:
�
> 0, i = 1,2,3.
}. Thus, S can be expressed as
(2.143)
(2.144)
associated with λ3, we deduce that
and
denote projection tensors introduced in (2.109) and (2.110) respectively. Finally, if all the three eigenvalues are equal, i.e., λ1 = λ2 = λ3 = λ, then
for U. If spectral representation of C is:
(2.148)
(2.149)
(2.150)
associated with λ3 then
























