Strain Tensors
Now, we shall look at the concept of strain. This is some quantity defined by us and hence there are various definitions of the same. Also, as we shall see later, we can develop the constitutive relation independent of these definitions. Experimental observations show that relative displacement of particles alone gives raise to stress. A measure of this relative displacement is the stretch ratio. However, this measure has the drawback that when the body is not deformed the stretch ratio is 1 (by virtue of the deformed length being same as the original length) and hence thought to be inconvenient to formulate constitutive relations. Consequently, another measure of relative displacement is sought which would be 0 when the body is not deformed and less than zero when compressed and greater than zero when stretched. This measure is called as the strain, ∈(A) . There is no unique way of obtaining the strain from the stretch ratio. The following functions satisfy the requirement of the strain:
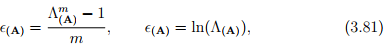
where m is some real number and ln stands for natural logarithm. Thus, if m = 1 in (1.5a) then the resulting strain is called as the engineering strain, if m = −1, it is called as the true strain, if m = 2 it is Cauchy-Green strain. The second function wherein ∈(A) = ln(λ(A)), is called as the Hencky strain or the logarithmic strain. Let us start by looking at the case when m = 2 in equation (3.81), that is the case,

Substituting (3.60) in (3.82) we obtain

where, E = 0.5[C − 1], is called the Cauchy-Green strain tensor. Thus, Cauchy-Green strain tensor carries information about the strain in the material fibers initially oriented along a given direction. Substituting Lagrangian displacement gradient, defined in (3.33), for deformation gradient in the expression for E, we obtain
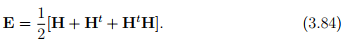
If tr(HHt ) << 1, i.e., each of the components of H is close to zero4 , then we can compute E approximately as

4Realize that tr(HHt ) = 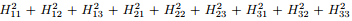 |
∈L is called as the Lagrangian linearized strain and will be used extensively while studying linearized elasticity.
Next, we examine the case when m = 1, in equation (3.81), that is the case,

Substituting (3.60) in (3.86) we obtain

Substituting Lagrangian displacement gradient, defined in (3.33), for deformation gradient in the expression for C and using the definition (3.85) for Lagrangian linearized strain, equation (3.87) evaluates to
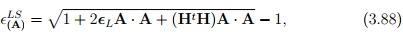
which when the components of the Lagrangian displacement gradient are small could be approximately computed as
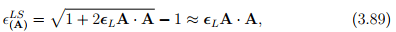
where we have approximately evaluated the square root using Taylor’s series5 . Thus, Lagrangian linearized strain carries the information on changes in length of material fibers initially oriented along a given direction when the changes in length are small. Instead of studying the strain in fibers oriented initially along a given direction, one can also study strains in fibers finally oriented along a given direction, a. Now, again the following functions satisfy the requirement of the strain:
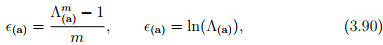
where m is some real number and ln stands for natural logarithm. We study the case when m = −2 in equation (3.90), that is the case,

Substituting (3.64) in (3.91) and rearranging we obtain
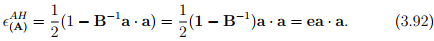
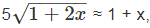 when x is small. when x is small. |
where, e = 0.5[1 − B−1 ], is called the Almansi-Hamel strain tensor and carries information about the strain in the material fibers finally oriented along a given direction. Substituting Eulerian displacement gradient, defined in (3.34), for F−1 in the expression for e, we obtain

If tr(hht ) << 1, then we can compute e approximately as

∈E is called as the Eulerian linearized strain. The Lagrangian and Eulerian displacement gradients are related through the equation
H = h + hH, (3.95)
obtained from the requirement that FF−1 = 1 and substituting the expressions (3.33) and (3.34) for F and F−1 respectively. It immediately transpires that when each of the components of H and h are close to zero then H ≈ h and hence both the Lagrangian and Eulerian linearized strain are numerically the same. Hence, when the distinction is not important the subscript, L or E would be dropped and the linearized strain denoted as ∈
There are other strain measures called the Hencky strain tensor in the Lagrangian and Eulerian form defined as ln(U) and ln(V) respectively. This strain tensor corresponds the case where the strain along a given direction is defined as the natural logarithm of the corresponding stretch ratio. Hencky strain is also sometimes called as the logarithmic strain.



















