Yield Line Theory for Slabs - Civil Engineering (CE) PDF Download

Yield Line Theory for Slabs
» Loads and load effects

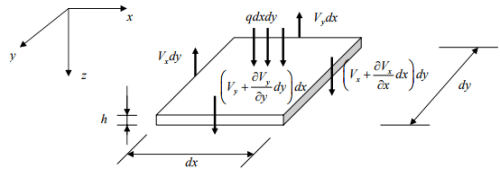
                       Surface and shear forces


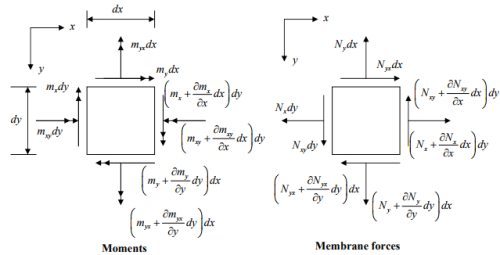
o Load effects to be solved: V_x ,V_y , m_x , m_y , m_xy , m_yx  , N_x , N_y , N_xy , N_yx ,
→ Ten unknowns and six equations
→ Indeterminate problem: We need to include stress-strain relation for complete elastic solution.

o The relative importance of the load effects is related to the thickness of the slab. Most reinforced and prestressed concrete floor slabs fall within “medium-thick” class, i.e., plates are
→ thin enough that shear deformations are small, and
→ thick enough that in-plane or membrane forces are small.

» Analysis methods:
o Elastic theory
o Elastic-plastic analysis
– Finite element analysis (FEA)
o Approximate methods of analysis
o Limit analysis – Yield Line Theory
– Lower & upper bound analysis
 

» Elastic theory
o Lagrange’s fourth-order PDE governing equation of isotropic plates loaded normal to their plane:

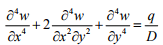
where w = deflection of plate in direction of loading at point ( x , y ).
q = loading imposed on plate per unit area, q ≈ f ( x , y )
D = flexural rigidity of plate,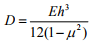
E = Young’s modulus
h = plate thickness
µ = Poisson’s ratio.

o Navier’s solution of Lagrange’s equation using doubly infinite Fourier series:

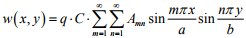
where
a,b = lengths of panel sides
m, n = integers ,
C, A_mn= constants – Boundary conditions.

» Finite difference (FD) method
o It replaces Lagrange’s fourth-order PDE with a series of simultaneous linear algebraic equations for the deflections of a finite number of points on the slab surface. Deflections, moments, and shears are computed.

» Finite element (FE) method
o It utilizes discretization of the physical system into elements. Displacement functions are chosen. Exact compatibility and approximate equilibrium considerations are used. ‰ Approximate methods
o Direct design method
o Equivalent frame method
o Assignment of moments
 

» Types of slabs
o According to the structural action

–– One-way slabs
–– Two-way slabs


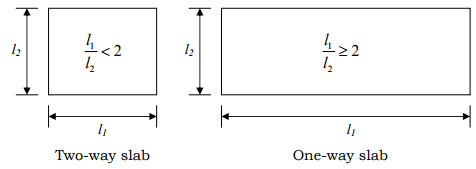
o According to the support and boundary conditions

» Choice of slab type
» Limit analysis – Yield Line Theory
o Ductility and Yield Line Theory
o Yield Line Analysis: Yield line theory permits prediction of the ultimate load of a slab system by postulating a collapse mechanism which is compatible with the boundary conditions. Slab sections are assumed to be ductile enough to allow plastic rotation to occur at critical section along yield lines.
1. Postulate a collapse mechanism compatible with the boundary conditions
2. Moment at plastic hinge lines ≈ Ultimate moment of resistance of the sections
3. Determine the ultimate load
4. Redistributions of bending moments are necessary with plastic rotations.

o Moment-curvature relationship
– Curvature ductility factor: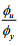 
– ε_E <<ε _Plastic 
– M_u ≈ constant at yield lines.

o Determinate structures → mechanism
o Indeterminate structures – moment redistribution
o Assumptions and guidelines for establishing axes of rotation and yield lines
o Determination of the ultimate load (or moment):
– Equilibrium method
– Analysis by Principle of Virtual Work

» Isotropic and orthotropic slabs
o Isotropic slabs A slab is said to be isotropically reinforced if it is reinforced identically in orthogonal directions and its ultimate resisting moment is the same in these two directions as it is along any line regardless of its direction.

o Orthotropic slabs A slab is said to be orthotropically reinforced if its ultimate strengths are different in two perpendicular directions. In such cases, yield lines will occur across these orthogonal directions.

o Determination of the moment capacity M_u for orthotropic slabs
Computation for the moment capacity M_u consistent with the yield line given the moment capacities M_x and M_y in the direction of the reinforcing bars:


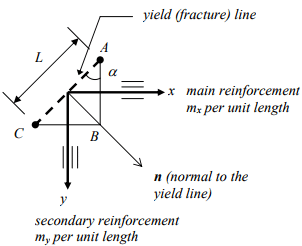
m_x = ultimate resisting moment per length along the x axis
m_y = ultimate resisting moment per length along the y axis
m_n = ultimate resisting moment per length along AC
m_nt = ultimate resisting moment per length along normal direction to the yield line (torsion)

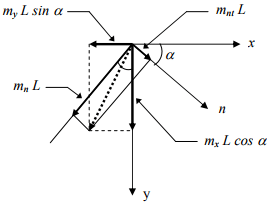
o Equilibrium in vector notation
  m_x (AB) = m_x L cos α
m_y (BC) = m_x L sin α
m_n (AC) = m_n L
m_nt (AC) = m_nt L

m_n L = ( mx L cos α ) cos α +
           ( m_y L sin α ) sin α
m_n = m_x cos² α + m_y sin² α
m_nt L = ( m_x L cos α ) sin α -
            ( m_y L sin α ) cos α
m_nt = ( m_x - m_y ) L sin α cos α

if α = 0 or π/2, then m_nt =0
if m_x = m_y = m, then
m_n = m (cos² α + sin² α ), m_nt =0
m_n = m

Square yield criterion (isotropic reinforcement)
if m_x ≠ m_y, then
orthogonally anisotropic or orthotropic

Orthotropic slabs can be reduced to equivalent isotropic cases by modifying the slab dimensions.

Buyukozturk Outline 11 In analyzing orthotropic plates it is usually easier to deal separately with the x and y direction components of the internal work done by the ultimate moments: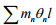
 

o Components of internal work done:


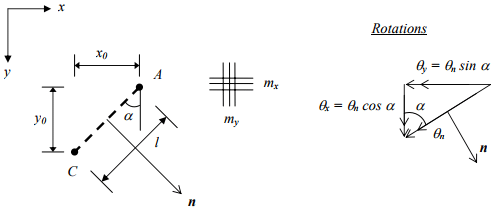
Equilibrium:


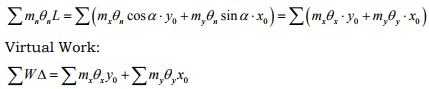
» Upper-Bound Solution (Energy Approach)
o Energy method, with an initial selection of a collapse mechanism, gives an upper bound solution, i.e., if failure mode (mechanism) is chosen incorrectly (still satisfying boundary condition) the solution for the ultimate load will be unconservative. The method involves:
• Select a failure (collapse) mechanism which satisfies the displacement boundary conditions everywhere (kinematic admissibility), and which satisfies the yield criterion at the yield line.
• Impose the condition that work done by the external loads must equal the work done by the resisting forces.
• If the correct mechanism is chosen the method leads to the correct value, otherwise, the predicted load is unconservative.
• This is explained with the following example: A fixed ended beam has a positive and negative moment capacity of M_u . Assume the following collapse mechanism,



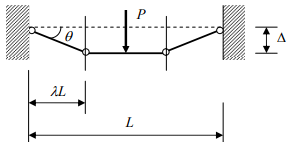
Conservation of energy:


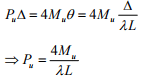
The correct collapse load is found for 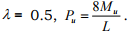   For any other value of λ < 0.5, P_u is unconservative.

» Comments on yield line theory:
1. In the equilibrium method, equilibrium of each individual segment of the yield pattern under the action of its bending and torsional moments, shear forces and external loads is considered.
2. In the virtual work method, shear force and torsional moment magnitudes and distribution need not be known because they do not work when summed over the whole slab when the yield line pattern is given a small displacement.

» Limitations on yield line theory:
1. Analysis is based on rotation capacity at the yield line, i.e., lightly reinforced slabs.
2. The theory focuses attention on the moment capacity of the slab. It is assumed an earlier failure would not occur due to shear, bond, etc.
3. The theory does not give any information on stresses, deflections, or service load conditions.