Rigid pavement as per IRC 58-2002
Rigid pavements are generally used in constructing airports and major highways, such as those in the interstate highway system. In addition, they commonly serve as heavy-duty industrial floor slabs, port and harbor yard pavements, and heavy-vehicle park or terminal pavements. Like flexible pavements, rigid highway pavements are designed as all-weather, long-lasting structures to serve modern day high-speed traffic. Offering high quality riding surfaces for safe vehicular travel, they function as structural layers to distribute vehicular wheel loads in such a manner that the induced stresses transmitted to the subgrade soil are of acceptable magnitudes.
Portland cement concrete (PCC) is the most common material used in the construction of rigid pavement slabs. The reason for its popularity is due to its availability and the economy. Rigid pavements must be designed to endure frequently repeated traffic loadings. The typical designed service life of a rigid pavement is between 30 and 40 years, lasting about twice as long as a flexible pavement.
One major design consideration of rigid pavements is reducing fatigue failure due to the repeated stresses of traffic. Fatigue failure is common among major roads because a typical highway will experience millions of wheel passes throughout its service life. In addition to design criteria such as traffic loadings, tensile stresses due to thermal energy must also be taken into consideration. As pavement design has progressed, many highway engineers have noted that thermally induced stresses in rigid pavements can be just as intense as those imposed by wheel loadings. Due to the relatively low tensile strength of concrete, thermal stresses are extremely important to the design considerations of rigid pavements.
Rigid pavements are generally constructed in three layers - a prepared subgrade, base or subbase, and a concrete slab. The concrete slab is constructed according to a designed choice of plan dimensions for the slab panels, directly influencing the intensity of thermal stresses occurring within the pavement. In addition to the slab panels, temperature reinforcements must be designed to control cracking behavior in the slab. Joint spacing is determined by the slab panel dimensions.
Three main types of concrete pavements commonly used are Jointed plain concrete pavement (JPCP), jointed reinforced concrete pavement (JRCP), and continuously reinforced concrete pavements (CRCP). JPCP‟s are constructed with contraction joints which direct the natural cracking of the pavement. These pavements do not use any reinforcing steel. JRCP‟s are constructed with both contraction joints and reinforcing steel to control the cracking of the pavement. High temperatures and moisture stresses within the pavement creates cracking, which the reinforcing steel holds tightly together. At transverse joints, dowel bars are typically placed to assist with transferring the load of the vehicle across the cracking. CRCP‟s solely rely on continuous reinforcing steel to hold the pavement‟s natural transverse cracks together. Prestressed concrete pavements have also been used in the construction of highways; however, they are not as common as the other three. Prestressed pavements allow for a thinner slab thickness by partly or wholly neutralizing thermally induced stresses or loadings.
Rigid Pavement Overlay Design
Near the end of a rigid pavement's service life, a decision must be made to either fully reconstruct the worn pavement, or construct an overlay layer. Considering an overlay can be constructed on a rigid pavement that has not reached the end of its service life, it is often more economically attractive to apply overlay layers more frequently. The required overlay thickness for a structurally sound rigid pavement is much smaller than for one that has reached the end of its service life. Rigid and flexible overlays are both used for rehabilitation of rigid pavements such as JPCP, JRCP, and CRCP.
There are three subcategories of rigid pavement overlays that are organized depending on the bonding condition at the pavement overlay and existing slab interface.
1. Bonded overlays
2. Unbonded overlays
3. Partially bonded overlays
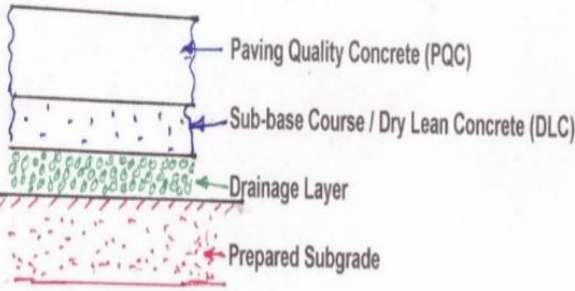
Rigid pavement
Rigid pavement- Westergaard‟s equations for load and temperature stresses- Examples- Design of slab thickness only as per IRC:58-2002.Rigid pavements have sufficient flexural strength to transmit the wheel load stresses to a wider area below. Compared to flexible pavement, rigid pavements are placed either directly on the prepared sub-grade or on a single layer of granular or stabilized material. Since there is only one layer of material between the concrete and the sub-grade, this layer can be called as base or sub-base course. In rigid pavement, load is distributed by the slab action, and the pavement behaves like an elastic plate resting on a viscous medium (Figure). Rigid pavements are constructed by Portland cement concrete (PCC) and should be analysed by plate theory instead of layer theory, assuming an elastic plate resting on viscous foundation. Plate theory is a simplified version of layer theory that assumes the concrete slab as a medium thick plate which is plane before loading and to remain plane after loading Bending of the slab due to wheel load and temperature variation and the resulting tensile and flexural stress Failure criteria of rigid pavements Fatigue cracking has long been considered as the ma jor, or only criterion for rigid pavement design. The allowable number of load repetitions to cause fatigue cracking depends on the stress ratio between flexural tensile stress and concrete modulus of rupture. Of late, pumping is identified as an important failure criterion. Pumping is the ejection of soil slurry through the joints and cracks of cement concrete pavement, caused during the downward movement of slab under the heavy wheel loads. Other major types of distress in rigid pavements include faulting, spalling, and deterioration.
Rigid pavement design As the name implies, rigid pavements are rigid i.e, they do not flex much under loading like flexible pavements. They are constructed using cement concrete. In this case, the load carrying capacity is mainly due to the rigidity ad high modulus of elasticity of the slab (slab action). H. M. Westergaard is considered the pioneer in providing the rational treatment of the rigid pavement analysis.
Modulus of sub-grade reaction
Westergaard considered the rigid pavement slab as a thin elastic plate resting on soil subgrade, which is assumed as a dense liquid. The upward reaction is assumed to be proportional to the deflection. Base on this assumption, Westergaard defined a modulus of sub-grade reaction K in kg/cm3 given by 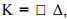 where Δ is the displacement level taken as 0.125 cm and p is the pressure sustained by the rigid plate of 75 cm diameter at a deflection of 0.125 cm.
where Δ is the displacement level taken as 0.125 cm and p is the pressure sustained by the rigid plate of 75 cm diameter at a deflection of 0.125 cm.
Relative stiffness of slab to sub-grade
A certain degree of resistance to slab deflection is offered by the sub-grade. The sub-grade deformation is same as the slab deflection. Hence the slab deflection is direct measurement of the magnitude of the sub-grade pressure. This pressure deformation characteristics of rigid pavement lead Westergaard to the define the term radius of relative stiffness l in cm is given by the equation below.
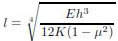
where E is the modulus of elasticity of cement concrete in kg/cm2 (3.0×105), μ is the Poisson‟s ratio of concrete (0.15), h is the slab thickness in cm and K is the modulus of subgrade reaction.
Critical load positions
Since the pavement slab has finite length and width, either the character or the intensity of maximum stress induced by the application of a given traffic load is dependent on the location of the load on the pavement surface. There are three typical locations namely the interior, edge and corner, where differing conditions of slab continuity exist. These locations are termed as critical load positions Equivalent radius of resisting section When the interior point is loaded, only a small area of the pavement is resisting the bending moment of the plate. Westergaard‟s gives a relation for equivalent radius of the resisting section in cm in the equation below.
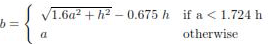
where a is the radius of the wheel load distribution in cm and h is the slab thickness in cm Wheel load stresses - Westergaard‟s stress equation The cement concrete slab is assumed to be homogeneous and to have uniform elastic properties with vertical sub-grade reaction being proportional to the deflection. Westergaard developed relationships for the stress at interior, edge and corner regions, denoted as σi , σe , σc in kg/cm2 respectively and given by the equations below.
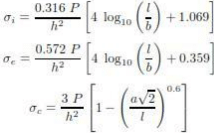
where h is the slab thickness in cm, P is the wheel load in kg, a is the radius of the wheel load distribution in cm, l the radius of the relative stiffness in cm and b is the radius of the resisting section in cm.

Critcal stress locations
Temperature stresses
Temperature stresses are developed in cement concrete pavement due to variation in slab temperature. This is caused by (i) daily variation resulting in a temperature gradient across the thickness of the slab and (ii) seasonal variation resulting in overall change in the slab temperature. The former results in warping stresses and the later in frictional stresses.
Warping Stress
The warping stress at the interior, edge and corner regions, denoted as σti , σte , σtc in kg/cm2 respectively and given by the equations.
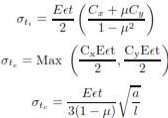
where E is the modulus of elasticity of concrete in kg/cm2 (3×105), is the thermal coefficient of concrete per o C (1×107) t is the temperature difference between the top and bottom of the slab, Cx and Cy are the coefficient based on Lx/l in the desired direction and Ly /l right angle to the desired direction, μ is the Poisson‟s ration (0.15), a is the radius of the contact area and l is the radius of the relative stiffness.
Warping Stress are developed in C C pavement at different location :
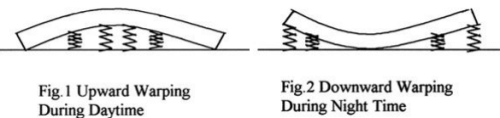
During the day time when the slab is warped with convex upwards (Fig.l), the foundation pulls the slab down by spring action, the characteristic of the Winkler foundation. The stresses caused by the hypothetical tension in the spring are assumed to represent the curling or warping stress caused by self-weight of the slab. If the foundation is stiffer, the curling stress is large because the restraining force of the hypothetical spring foundation is also large though weight of the slab remains the same. The greater the temperature difference between the top and the bottom of the slab, greater is the warping and a large tension in the spring causes higher stresses. During the night hours, the slab curls as shown in Fig. 2. This condition is critical during the early life of concrete when it is very weak. Curling stresses are sensitive to the stiffness of the idealised foundation. Author‟s analysis shows that a concrete a slab laid on a Dry Lean Concrete (DLC) sub-base warps up and leave the foundation even for a temperature difference of 10°C between the top and the bottom of the slab and the self weight of the slab is not large enough to deflect the slab to make it rest on the foundation. Any higher temperature difference causes additional warping but does not cause any additional curling stresses since the self-weight remains the same.
Frictional stresses
The frictional stress σf in kg/cm2 is given by the equation
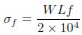
where W is the unit weight of concrete in kg/cm2 (2400), f is the coefficient of sub grade friction (1.5) and Lis the length of the slab in meters.
Combination of stresses
The cumulative effect of the different stress give rise to the following thee critical cases
• Summer, mid-day: The critical stress is for edge region given by σcritical = σe + σte − σf
• Winter, mid-day: The critical combination of stress is for the edge region given by σcritical = σe + σte + σf
• Mid-nights: The critical combination of stress is for the corner region given by σcritical = σc + σtc
where Δ is the displacement level taken as 0.125 cm and p is the pressure sustained by the rigid plate of 75 cm diameter at a deflection of 0.125 cm.






















