Introduction to Compressible Flow - 1 | Fluid Mechanics for Mechanical Engineering PDF Download
Introduction
- Compressible flow is often called as variable density flow. For the flow of all liquids and for the flow of gases under certain conditions, the density changes are so small that assumption of constant density remains valid.
- Let us consider a small element of fluid of volume
The pressure exerted on the element by the neighbouring fluid is p . If the pressure is now increased by an amount dp , the volume of the element will correspondingly be reduced by the amount d
The compressibility of the fluid K is thus defined as
However, when a gas is compressed, its temperature increases. Therefore, the above mentioned definition of compressibility is not complete unless temperature condition is specified. When the temperature is maintained at a constant level, the isothermal compressibility is defined as
(38.2)
- Compressibility is a property of fluids. Liquids have very low value of compressibility (for ex. compressibility of water is 5 ´ 10-10 m2/N at 1 atm under isothermal condition), while gases have very high compressibility (for ex. compressibility of air is 10-5 m2/N at 1 atm under isothermal condition).
- If the fluid element is considered to have unit mass and v is the specific volume (volume per unit mass) , the density is
In terms of density; Eq. (38.1) becomes
(38.3)
We can say that from Eqn (38.1) for a change in pressure, dp, the change in density is
If we also consider the fluid motion, we shall appreciate that the flows are initiated and maintained by changes in pressure on the fluid. It is also known that high pressure gradient is responsible for high speed flow. However, for a given pressure gradient dp , the change in density of a liquid will be much smaller than the change in density of a gas (as seen in Eq. (38.4))
So, for flow of gases, moderate to high pressure gradients lead to substantial changes in the density. Due to such pressure gradients, gases flow with high velocity. Such flows, where 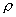 is a variable, are known as compressible flows.
is a variable, are known as compressible flows.
- Recapitulating Chapter 1, we can say that the proper criterion for a nearly incompressible flow is a small Mach number,
- In this chapter we shall treat compressible flows which have Mach numbers greater than 0.3 and exhibit appreciable density changes. The Mach number is the most important parameter in compressible flow analysis. Aerodynamicists make a distinction between different regions of Mach number.
Categories of flow for external aerodynamics.
- Ma < 0.3: incompressible flow; change in density is negligible.
- 0.3< Ma < 0.8: subsonic flow; density changes are significant but shock waves do not appear.
- 0.8< Ma < 1.2: transonic flow; shock waves appear and divide the subsonic and supersonic regions of the flow. Transonic flow is characterized by mixed regions of locally subsonic and supersonic flow
- 1.2 < Ma < 3.0: supersonic flow; flow field everywhere is above acoustic speed. Shock waves appear and across the shock wave, the streamline changes direction discontinuously.
- 3.0< Ma : hypersonic flow; where the temperature, pressure and density of the flow increase almost explosively across the shock wave.
- For internal flow, it is to be studied whether the flow is subsonic ( Ma < 1) or supersonic (Ma > 1). The effect of change in area on velocity changes in subsonic and supersonic regime is of considerable interest. By and large, in this chapter we shall mostly focus our attention to internal flows.
Perfect Gas
- A perfect gas is one in which intermolecular forces are neglected. The equation of state for a perfect gas can be derived from kinetic theory. It was synthesized from laboratory experiments by Robert Boyle, Jacques Charles, Joseph Gay-Lussac and John Dalton. For a perfect gas, it can be written
where p is pressure ( N/m2 ),is the volume of the system (m3 ), M is the mass of the system (kg), R is the characteristic gas constant (J/kg K) and T is the temperature ( K ). This equation of state can be written as
where v is the specific volume (m3/kg). Also,
where is the density (kg/m3 ).
- In another approach, which is particularly useful in chemically reacting systems, the equation of state is written as
where N is the number of moles in the system, and is the universal gas constant which is same for all gases
- Recall that a mole of a substance is that amount which contains a mass equal to the molecular weight of the gas and which is identified with the particular system of units being used. For example, in case of oxygen (O2), 1 kilogram-mole (or kg. mol) has a mass of 32 kg. Because the masses of different molecules are in the same ratio as their molecular weights; 1 mol of different gases always contains the same number of molecules, i.e. 1 kg-mol always contains 6.02 ×1026 molecules, independent of the species of the gas. Dividing Eq. (38.9) by the number of moles of the system yields
Vol. per unit mole
If Eq. (38.9) is divided by the mass of the system, we can write
where v is the specific volume as before and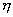 is the mole-mass ratio (kg- mol/kg). Also, Eq. (38.9) can be divided by system volume, which results in
is the mole-mass ratio (kg- mol/kg). Also, Eq. (38.9) can be divided by system volume, which results in
where C is the concentration (kg - mol/m3 )
- The equation of state can also be expressed in terms of particles. If NA is the number of molecules in a mole (Avogadro constant, which for a kilogram- mole is 6.02 ×1026 particles), from Eq. (38.12) we obtain
In the above equation, NAC is the number density, i.e. number of particles per unit volume andis the gas constant per particle, which is nothing but Boltzmann constant.
Finally, Eq. (38.13) can be written as
where n: number density
 : Boltzmann constant.
: Boltzmann constant.
- It is interesting to note that there exist a variety of gas constants whose use depends on the equation in consideration.
1.Universal gas constant- When the equation deals with moles, it is in use. It is same for all the gases.
= 8314 J/( Kg-mol-K)
2.Characteristic gas constant- When the equation deals with mass, the characteristic gas constant (R) is used. It is a gas constant per unit mass and it is different for different gases. As such , where M is the molecular weight. For air at standard conditions,
R = 287 J/(kg-K)
3.Boltzmann constant- When the equation deals with molecules, Boltzmann constant is used. It is a gas constant per unit molecule.
K = 1.38 X 10 -23J / K
Application of the perfect gas theory
a. It has been experimentally determined that at low pressures (1 atm or less) and at high temperature (273 K and above), the value of ( the well known compressibility z, of a gas) for most pure gases differs from unity by a quanity less than one percent ( the well known compressibility z, of a gas).
b. Also, that at very low temperatures and high pressures the molecules are densely packed. Under such circumstances, the gas is defined as real gas and the perfect gas equation of state is replaced by the famous Van-der-Waals equation which is
where a and b are constants and depend on the type of the gas.
In conclusion, it can be said that for a wide range of applications related to compressible flows, the temperatures and pressures are such that the equation of state for the perfect gas can be applied with high degree of confidence
Internal Energy and Enthalpy
- Microscopic view of a gas is a collection of particles in random motion. Energy of a particle consists of translational energy, rotational energy, vibrational energy and specific electronic energy. All these energies summed over all the particles of the gas, form the specific internal energy, e , of the gas.
- Imagine a gas in thermodynamic equilibrium,i.e., gradients in velocity, pressure, temperature and chemical concentrations do not exist.
Then the enthalpy, h , is defined as h = e + pu, where u is the specific volume.
If the gas is not chemically reacting and the intermolecular forces are neglected, the system can be called as a thermally perfect gas, where internal energy and enthalpy are functions of temperature only. One can write
For a calorically perfect gas,
Please note that in most of the compressible flow applications, the pressure and temperatures are such that the gas can be considered as calorically perfect.
- For calorically perfect gases, we assume constant specific heats and write
cp - cv = R (38.19)
- The specific heats at constant pressure and constant volume are defined as
Equation (38.19), can be rewritten as
Also So we can rewrite Eq. (38.21) as
In a similar way, from Eq. (38.19) we can write
First Law of Thermodynamics
- Let us imagine a control-mass system with a fixed mass of gas. If δq amount of heat is added to the system across the system-boundary and if δw is the work done on the system by the surroundings, then there will be an eventual change in internal energy of the system which is denoted by de and we can write
de = δq + δw
This is first law of thermodynamics. Here, de is an exact differential and its value depends only on initial and final states of the system. However, 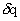 and
and 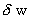 are dependent on the path of the process. A process signifies the way by which heat can be added and the work is done on/by the system. (Note that heat added to system is taken as positive and work done on the system is taken as positive)
are dependent on the path of the process. A process signifies the way by which heat can be added and the work is done on/by the system. (Note that heat added to system is taken as positive and work done on the system is taken as positive)
- In this chapter we are interested in isentropic process which is a combination of adiabatic (no heat is added to or taken away from the system) and reversible process (occurs through successive stages, each stage consists of an infinitesimal small gradient and is an equilibrium state). In an isentropic process, entropy of a system remains constant ( as seen in the following lecture).
|
56 videos|106 docs|75 tests
|
FAQs on Introduction to Compressible Flow - 1 - Fluid Mechanics for Mechanical Engineering
| 1. What is compressible flow in mechanical engineering? |  |
| 2. What are the key differences between compressible flow and incompressible flow? |  |
| 3. What are some applications of compressible flow in mechanical engineering? |  |
| 4. How is compressible flow analyzed and modeled in mechanical engineering? |  |
| 5. What are some challenges faced in dealing with compressible flow in mechanical engineering? |  |



















