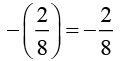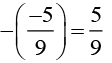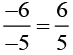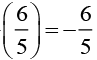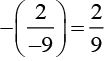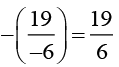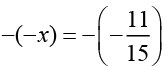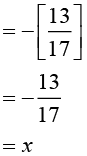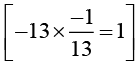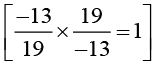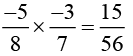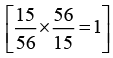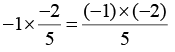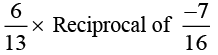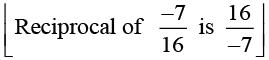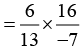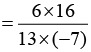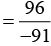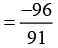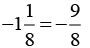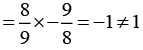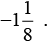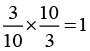NCERT Solutions for Class 8 Maths Chapter 1 - Rational Numbers (Exercise 1.1)
Rational numbers are numbers that can be expressed as the ratio or fraction of two integers, where the denominator is not zero. Examples of rational numbers include:
- 1/2
- 5/7
- -3/4
- 0 (since it can be expressed as 0/1)
Let's have a look at the NCERT Solutions of Class 8 Mathematics Chapter "Rational Numbers"

Exercise 1.1
Q1. Name the property under multiplication used in each of the following:
(i) -4/5 × 1 = 1 × (-4/5) = -4/5
Ans: Since, 1 is the multiplicative identity.
∴ 1 is the multiplicative identity and here, property of multiplicative identity is used.
(ii) -13/17 × (-2/7) = -2/7 × (-13/17)
Ans: The property of commutativity is used in the equation.
(iii) -19/29 × 29/-19 = 1
Ans: The multiplicative inverse is the property used in this equation.
Q2. Tell what property allows you to compute 1/3 × (6 × 4/3) as (1/3 × 6) × 4/3.
Ans: 1/3 × (6 × 4/3) = (1/3 × 6) × 4/3
Here, the way in which factors are grouped in a multiplication problem supposedly does not change the product.
Hence, the Associativity Property is used here.
Q3. The product of two rational numbers is always a _______.
Ans:The product of two rational numbers is always a rational number.
Let's consider two rational numbers: 1/2 and 3/4.
When we multiply these two rational numbers,
(1/2) * (3/4) = (1 * 3) / (2 * 4) = 3/8
Here, the product of 1/2 and 3/4 is 3/8, which is also a rational number. Therefore, this example demonstrates that the product of two rational numbers is always a rational number.
Deleted Questions from NCERT
Q.1. Using appropriate properties find:
(i) 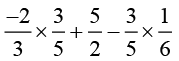
(ii) 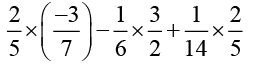
Difficulty Level: Easy
What is the known/given?
Rational numbers with addition subtraction and multiplication.
What is the unknown?
Result of addition, subtraction and multiplication of rational numbers.
Reasoning:By using commutativity of multiplication and addition getting the answer.
Solution (i):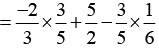
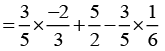 [By commutativity of multiplication]
[By commutativity of multiplication]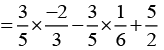 [Commutativity of addition]
[Commutativity of addition]
[Rearranging to take a common]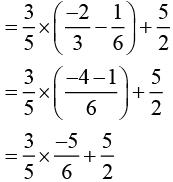
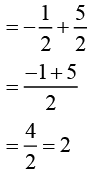
Answer (i): 2
Solution (ii):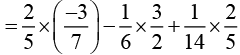
Rearranging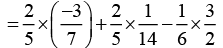
Taking 2/5 common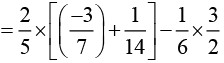 [by distributivity]
[by distributivity]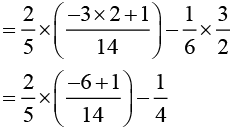
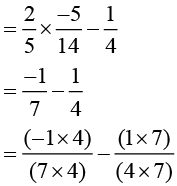
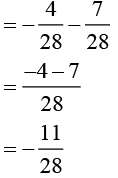
Answer (ii): 
Q.2. Write the additive inverse of each of the following
(i) 2/8
(ii) -5/9
(iii) -6/-5
(iv) 2/-9
(v) 19/-6
Difficulty Level: Easy
What is the known/given?
Rational numbers
What is the unknown?
Additive inverse
Reasoning:
The negative of a rational number is called additive inverse.
Solution:
(i) 2/8
Additive inverse of 2/8 is
(ii) -5/9
Additive inverse of -5/9 is
(iii) -6/-5
The rational number is
Additive inverse of -6/-5 is
(iv) 2/-9
Additive inverse of 2/-9 is
(v) 19/-6
Additive inverse of 19/-6 is
Q.3. Verify that − ( − x ) = x for
(i) x = 11/15
(ii) x =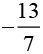
Difficulty Level: Easy
What is the known/given?
Rational number
What is the unknown?
The negative of the negative of a rational number.
Reasoning:
The negative of the negative of a rational number is that rational number of Self.
Solution:
(i) x = 11/15
= 11/15
= x
Proved.
(ii) x =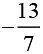
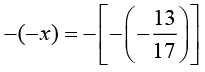
Proved.
Q.4. Find the multiplicative inverse of the following.
(i) −13
(ii) −13/19
(iii) 1/5
(iv) 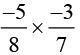
(v) 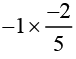
(vi) −1
Difficulty Level: Medium
What is the known/given?
Rational number
What is the unknown?
The multiplicative inverse.
Reasoning:The reciprocal of the given rational number is the multiplicative inverse. [the product of the rational number and its multiplicative inverse is 1]
Solution:
(i) −13
The Multiplicative inverse of −13 is -1/13
(ii) −13/19
The Multiplicative inverse of −13/19 is 19/-13
(iii) 1/5
The Multiplicative inverse of 1/5 is 5/1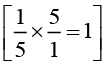
(iv) 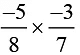
The Multiplicative inverse of 15/56 is 56/15
(v) 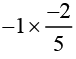
This can be simplified as:
= 2/5
The multiplicative inverse of 2/5 is 5/2
(vi) −1
The multiplicative inverse of −1 is −1.
(−1) x (-1) = 1
Q.5. Multiply 6/13 by the reciprocal of -7/16
Difficulty Level: Easy
What is the known/given?
Rational numbers
What is the unknown?
Product of the rational numbers.
Reasoning:
Reciprocal of a rational number is its multiplicative inverse.
Solution:
Answer:
Q6. Is 8/9 the multiplicative inverse of 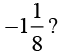 Why or why not?
Why or why not?
Difficulty Level: Medium
What is the known/given?
Rational numbers.
What is the unknown?
Multiplicative or not
Reasoning:The product of a rational number with its multiplicative inverse is 1.
Solution:
Now:
Answer:
So, 8/9 is not the multiplicative inverse of8/9 is not the multiplicative inverse of
because the product of 8/9 and
is -1, and it should be 1 to be a multiplicative inverse.
Q.7. Is 0.3 the multiplicative inverse of 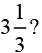 Why or why not?
Why or why not?
Difficulty Level: Medium
What is the known/given?
Rational number.
What is the unknown?
Multiplicative inverse or not?
Reasoning:The product of the rational number and its multiplicative inverse is 1.
Solution:0.3 can be written as 3/10
Given rational numbercan be written as 10/3
So,Answer:
Yes, 0.3 is the multiplicative inverse ofbecause their product is 1.
Q.8. Write:
(i) Rational number does not have a reciprocal
0 (zero) is the rational number which does not have a reciprocal.
(ii) The rational number that is equal to its reciprocals.
The rational numbers 1 and (–1) are equal to their own reciprocals.
(iii) The rational number that is equal to its negative.
Rational number 0 is equal to its negative.
Q.9. Fill in the blanks.
(i) Zero has ________ reciprocal.
Zero has no reciprocal
(ii) The numbers ________ and ________ are their own reciprocals
The numbers 1 and (–1) are their own reciprocals.
(iii) The reciprocal of –5 is ________.
The reciprocal of (–5) is 1/-5
(iv) Reciprocal of 1/x , where x ≠ 0 is ________.
Reciprocal of 1/x where x ≠ 0 is x .
(v) The reciprocal of a positive rational number is ________.
The reciprocal of a positive rational number is positive.
|
81 videos|413 docs|31 tests
|
FAQs on NCERT Solutions for Class 8 Maths Chapter 1 - Rational Numbers (Exercise 1.1)
| 1. What are rational numbers? |  |
| 2. What is the difference between rational and irrational numbers? |  |
| 3. How can you determine if a number is rational or irrational? |  |
| 4. How can rational numbers be used in real life? |  |
| 5. What is the importance of understanding rational numbers? |  |