NCERT Solutions for Class 8 Maths Chapter 2 - Ex 2.1 Linear Equations in One Variable
The linear equations in one variable is an equation which is expressed in the form of ax+b = 0 or ax+b= c, where x is a variable, a is the coefficient of x, b and c are constants
- For example, 2x+3=8 is a linear equation having a single variable in it. Therefore, this equation has only one solution, which is x = 5/2.
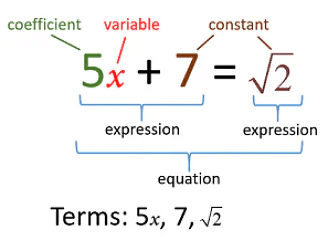
- Whereas if we speak about linear equations in two variables, it has two solutions.
Let's have a look at NCERT Solutions of Linear Equations in One Variable:
Solve the following equations
Q1. x – 2 = 7
Ans: Transposing (–2) to RHS, we have:
⇒ x = 7 + 2
∴ x = 9
Note: By transposing a term from one side to another side, we mean changing its sign and carrying it to the other side.
Q2. y + 3 = 10
Ans: Transposing 3 to RHS, we have:
⇒ y = 10 – 3
∴ y = 7
Q3. 6 = z + 2
Ans: Transposing 2 to LHS, we have:
⇒ 6 – 2 = z
⇒ 4 = z
∴ z = 4
Q4. (3/7) + x = (17/7)
Ans: Transposing 3/7 to RHS, we have: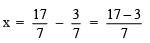
= 14/7
= 2
Q5. 6x = 12
Ans: Dividing both sides by 6, we have: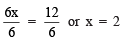
∴ x = 2
Q6. (t/5) = 10
Ans: Multiplying both sides by 5, we have:
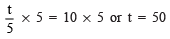
∴ t = 50
Q7. (2x/3) = 18
Ans: Multiplying both sides by 3, we have: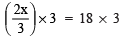
⇒ 2x = 54
Dividing both sides by 2, we have:
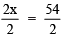
⇒ x = 54/2 = 27
∴ x = 27
Q8. 1.6 = (y/1.5)
Ans: Multiplying both sides by 1.5, we have:
⇒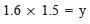
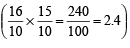
⇒ 2.4 = y
∴ y = 2.4
Q9. 7x – 9 = 16
Ans: Transposing (–9) to RHS, we have:
7x = 16 + 9 = 25
Dividing both sides by 7, we have:
∴ x = 25/7
Q10. 14y – 8 = 13
Ans: Transposing –8 to RHS, we have:
14y = 13 + 8 = 21
Dividing both sides by 14, we have:
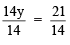
⇒
∴ y = 3/2
Q11. 17 + 6p = 9
Ans: Transposing 17 to RHS, we have:
6p = 9 – 17 = –8
Dividing both sides by 6, we have:
⇒
∴
Q12. (x/3) + 1 = (7/15)
Ans: Transposing 1 to RHS, we have:
⇒
Multiplying both sides by 3, we have:
∴ x = - 8/5
|
41 videos|48 docs|9 tests
|
FAQs on NCERT Solutions for Class 8 Maths Chapter 2 - Ex 2.1 Linear Equations in One Variable
| 1. What are linear equations in one variable? |  |
| 2. What are the methods to solve linear equations in one variable? |  |
| 3. How are linear equations in one variable used in real-life situations? |  |
| 4. What is the importance of learning linear equations in one variable? |  |
| 5. What are the common mistakes to avoid while solving linear equations in one variable? |  |






















