Points to Remember - Playing with Numbers | NCERT Textbooks & Solutions for Class 8 PDF Download
Points to Remember
• A two digit number can be written in generalized form as 10
• A three digit number can be written in generalized form as 100
• Generalized form of numbers are helpful in solving puzzles or number games.
• A number is divisible by 10, if its ones digits is 0.
• A number is divisible by 5, if its ones digits is 0 or 5.
• A number is divisible by 2, if its ones digits is 0, 2, 4, 6 or 8.
• A number is divisible by 9, if the sum of its digits is divisible by 9.
• A number is divisible by 3, if the sum of its digits is divisible by 3.
We Know That
Numbers are of various types such as natural numbers, whole numbers integers, fractional and rational numbers. They are full of fun and magic. We also know about the various divisibility tests of numbers. We can enjoy, the magic and wonder of numbers For example,
9 x 1 =
9 x 2 = 18 → 1 + 8 =
9 x 3 = 27 → 2 + 7 =
9 x 123 = 1107 → 1 + 1 + 0 + 7 =
1234 x 9 = 11106 → 1 + 1 + 1 + 0 + 6 =
12345 x 9 = 111105 → 1 + 1 + 1 + 1 + 0 + 5 =
123456 x 9 = 1111104 → 1 + 1 + 1 + 1 + 1 + 0 + 4 =
NUMBERS IN GENERAL FORM
We can express a number in general form using place value system, we may call it the expanded form of the number. Let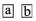 is a two digit number. We can write it in generalized form as
is a two digit number. We can write it in generalized form as Similarly, a 3-digit number
can be written as
Games with numbers
Reversing the digits (2-digit number)
Example: Sudaram considered any number of 2-digits.
Writing the given number in generalized form:
Reversing the digits and writing the new number in generalized form:
Adding, we get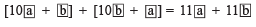
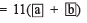
i.e. he got
11 x [Sum of the digits of the chosen number]
Reversing The Digits and Subtracting
Let Sundaram chooses a number
Generalised form =
Reversing the digits, new number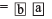
Generalised form =
Subtracting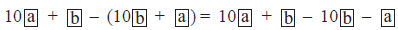 (when a > b)
(when a > b)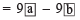
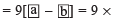 [Difference of the digits of the chosen number]
[Difference of the digits of the chosen number]
or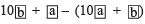 (when b > a)
(when b > a)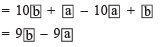
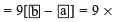 [Difference of the digits of the chosen number]
[Difference of the digits of the chosen number]
Reversing The Digits of A 3-Digit number
Note:
When we reverse the digits of a 3-digit number then the middle digit (i.e. tens digit) remains unchanged.
Letters for Digit
Note:
For problems of addition and multiplication, we follow the following rules while during various puzzles.
(i) Each letter in a puzzle must stand for just one digit and each must be represented by just one
letter.
(ii) The first digit of a number cannot be zero.
Example: Find A and B such that
Solution: We have to choose B such that B x 3 
It is possible for B = 0 or B = 5
Now, let us look for A,
If
A = 1, then AB x AB
10 x 13 = 130 For B = 0
or
15 x 13 = 195 For B = 5
which is less than 570 or 575
If A = 3, then
30 x 33 = 990 For B = 0
and
35 x 33 = 1155 For B = 5
which is greater than 570 or 575
If A = 2, then
20 x 23 = 460 For B = 0
and
25 x 23 = 575 For B = 5
The first possibility (20 x 23) fails but
The second one is correct
∴ The required values of A and B are
A = 2 and B = 5
Solve Examples:
Question 1. On multiplying 121 and its reverse, we get
a. 14641
b. 14541
c. 14441
d. None of the above.
Solution: A is the correct option. The reverse of 121 is 121, hence 121 × 121 = 14641.
Question 2. Which of the numbers are in general form?
a. 2 × 100 + 3 × 10 + 7
b. 2 × 10 + 3× 10 + 7
c. 2 × 100 + 2 × 100 + 7
d. 2 × 100 + 3 × 10 + 7
Solution: A is the correct option. The general form of any three digits is
abc = a× 100 + b × 10+ c
So, 237 = 2 × 100 + 3 × 10 + 7
So only one expression is in general form.
Question 3: The units digit of every prime number (other than 2 and 5 ) must be necessarily
a. 1, 3 0r 5
b. 1, 3, 7 or 9
c. 7 or 9
d. 1 or 7
Solution: B is the correct option.. All the even numbers are composite so prime numbers cannot end with any of the digits 0, 2, 4, 6, 8. Therefore units digit of every prime number (other than 2 and 5) must be necessarily 1, 3, 7 0r 9.
Question 4: Which of the following numbers is divisible by 14?
a. 4683
b. 7321
c. 1428
d. 5631
Solution: C is the correct option. The divisibility rule for 14 is that if the number is divisible by both 2 and 7 then the number is exactly divisible by 14. Here the last digit is, even so, the number 1428 is divisible by 2. 1428 is multiple of 7 so this number is also divisible by 7.
Question 5. Three common multiples of 18 and 16 are
a. 18, 6, 9
b. 18, 36, 6
c. 36, 54, 72
d. None
Solution: C is the correct option. The multiple of 18 is 18, 36 and 54. Multiples of 6 are 6, 12 and 18. Here the first common multiple will be 18. the next common multiple will be multiples of 18. The first three common multiples of 18 and 6 are 18, 36 and 54.
FAQs on Points to Remember - Playing with Numbers - NCERT Textbooks & Solutions for Class 8
| 1. What is the concept of playing with numbers in Class 8? |  |
| 2. What are some important topics covered in the Playing with Numbers chapter of Class 8? |  |
| 3. How can divisibility rules be used to determine if a number is divisible by another number? |  |
| 4. What is the importance of prime factorization in playing with numbers? |  |
| 5. How can playing with numbers concepts be applied in real-life situations? |  |














