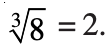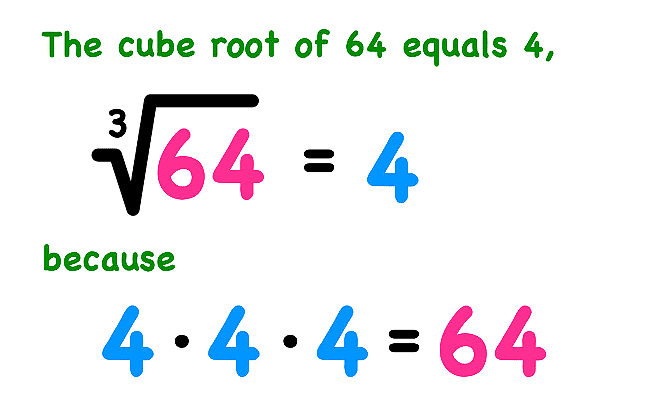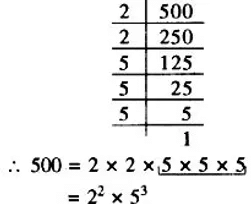 Cube of a number
Cube of a number
A natural number multiplied by itself three times gives a cube of that number, e.g.
1 × 1 × 1 = 1
2 × 2 × 2 = 8
3 × 3 × 3 = 27
4 × 4 × 4 = 64
The numbers 1, 8, 27, 64, … are called cube numbers or perfect cubes.
Perfect Cube: A number is a perfect cube if it can be expressed as n3 for some integer n.
Prime Factor Test: In the prime factorization of a perfect cube, every prime factor appears in groups of three.
Cube Root of a Number
The cube root of a number is the side length of a cube whose volume is that number.
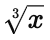
is the inverse operation of cubing x.
For example :
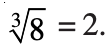
This means the cube root of 8 is 2.
Prime Factorization Method: Factorize the number, group identical factors in threes, and multiply one factor from each triplet to get the cube root.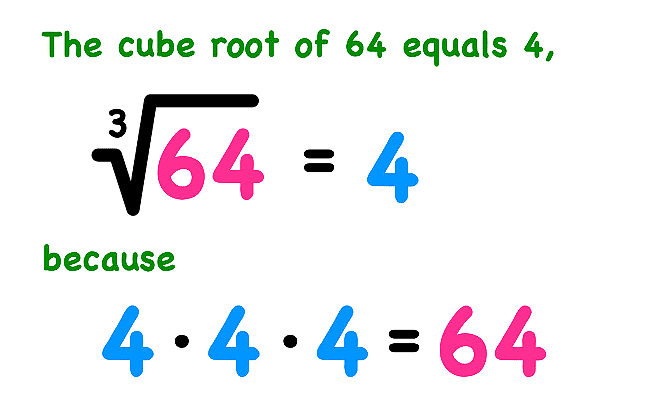
Steps to Calculate Cube Root
1. Prime Factorize the Number
Break the number down into its prime factors.
For example: Prime Factorize 8000
8000 = 2 × 2 × 2 × 2 × 2 × 2 × 5 × 5 × 5
2. Group the Factors in Threes
Arrange identical factors into sets of three.
8000 = (2 × 2 × 2) (2 × 2 × 2) (5 × 5 × 5)
3. Multiply One Factor from Each Triplet
From each group of three identical primes, take one prime and multiply them together.
8000 = (2 × 2 × 2) (2 × 2 × 2) (5 × 5 × 5)
Picking one prime from each triplet: 2 × 2 × 5 = 20
4. Result
The product you get in Step 3 is the cube root of the original number.
Therefore, cube root of 8000 is 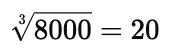
Question for Points to Remember - Cubes and Cube Roots
Try yourself:Which of the following statements is true about perfect cubes?
Explanation
- The statement in Option A is false. The cube of a negative number is always negative.
- The statement in Option B is false. The cube of an even number is always even.
- The statement in Option C is true. If the digit in the one's place of a number is 2, then the ending digit of its cube will be 8.
- The statement in Option D is false. The cube of a number ending in 5 will end in 5.
Therefore, the correct answer is Option C.
Report a problem
Properties of Perfect Cubes
(a) Property 1
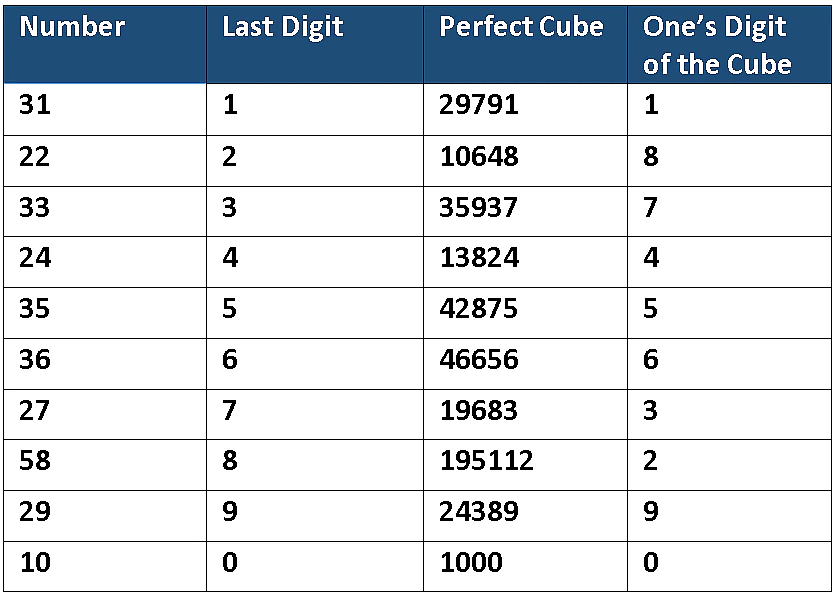
If the digit in the one’s place of a number is 0, 1, 4, 5, 6 or 9, then the digit in the one’s place of its cube will also be the same digit.
(b) Property 2
If the digit in the one’s place of a number is 2, the digit in the one’s place of its cube is 8, and vice-versa.
(c) Property 3
If the digit in the one’s place of a number is 3, the digit in the one’s place of its cube is 7 and vice-versa.
Examples of Properties 1, 2 & 3
(d) Property 4
Cubes of even natural numbers are even.
Examples of Property 4
(e) Property 5
Cubes of odd natural numbers are odd.
Examples of Property 5

(f) Property 6
Cubes of negative integers are negative.
Examples of Property 6
Some Interesting Patterns in Cubes
1. Adding consecutive odd numbers
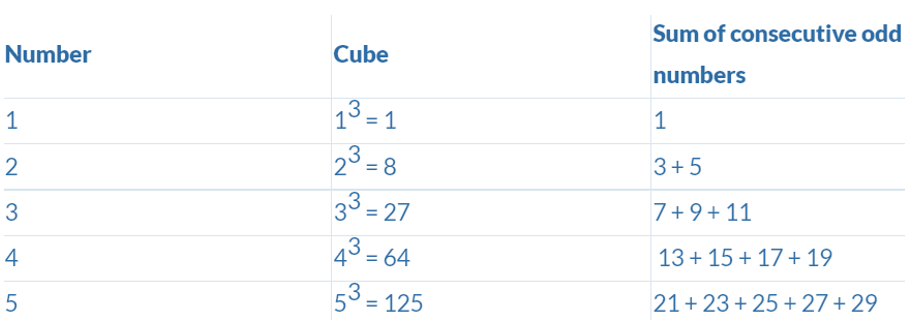
Note that we start with [n * (n – 1) + 1] odd number.
2. Difference of two consecutive cubes:
23 – 13 = 1 + 2 * 1 * 3
33 – 23 = 1 + 3 * 2 * 3
43 – 33 = 1 + 4 * 3 * 3
53 – 43 = 1 + 5 * 4 * 3
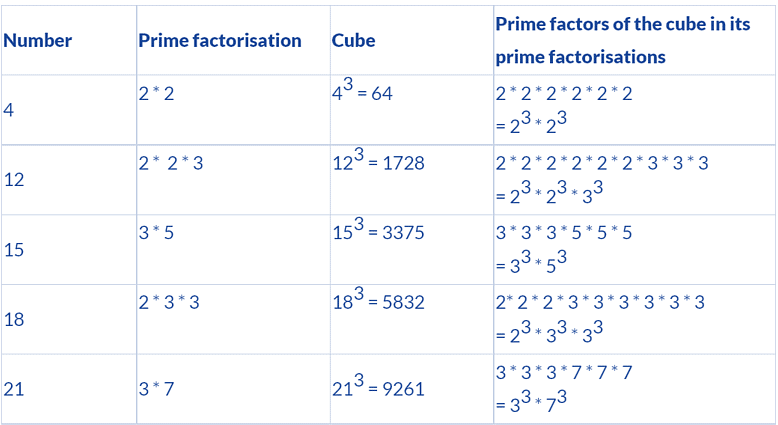
3. Cubes and their prime factor
Each prime factor of the number appears three times in its cube.
Facts That Matter
- If we multiply a number by itself three times, the product so obtained is called the perfect cube of that number.
- There are only 10 perfect cubes from 1 to 1000.
- Cubes of even numbers are even and those of odd numbers are odd.
- The cube of a negative number is always negative.
- If the prime factors of a number cannot be made into groups of 3, it is not a perfect cube.
Question for Points to Remember - Cubes and Cube Roots
Try yourself:
Which property states that the cubes of even natural numbers are even?Explanation
- Property 1 states that the digit in the one's place of a number and its cube will be the same.
- Property 2 states that if the digit in the one's place of a number is 2, the digit in the one's place of its cube is 8, and vice-versa.
- Property 4 states that cubes of even natural numbers are even.
- Property 6 states that cubes of negative integers are negative.
- Among these properties, Property 4 specifically mentions that cubes of even natural numbers are even.
Report a problem
Solved Examples
Example 1: Is 500 a perfect cube?
Solution:
500 = 5 * 5 * 5 * 2 * 2
∵ In the above prime factorisation 2 * 2 remain after grouping the prime factors in triples.
∴ 500 is not a perfect cube.
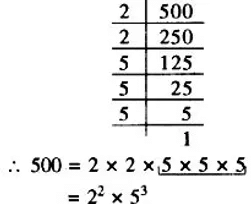
Example 2: Is 1372 a perfect cube? If not, find the smallest natural number by which 1372 must be multiplied so that the product is a perfect cube.
Solution:
We have 1372 = 2 * 2 * 7 * 7 * 7
Since, the prime factor 2 does not appear in a group of triples.
∴ 1372 is not a perfect cube.
Obviously, to make it a perfect cube we need one more 2 as its factor.
i.e. [1372] * 2 = [2 * 2 * 7 * 7 * 7] * 2
or
2744 = 2 * 2 * 2 * 7 * 7 * 7
which is a perfect cube.
Thus, the required smallest number = 2.

Example 3: Is 31944 a perfect cube? If not then by which smallest natural number should 31944 be divided so that the quotient is a perfect cube?
Solution:
We have 31944 = 2 * 2 * 2 * 3 * 11 * 11 * 11
Since, the prime factors of 31944 do not appear in triples as 3 is left over.
∴ 31944 is not a perfect cube. Obviously, 31944 / 3 will be a perfect cube
i.e. [31944] ÷3 = [2 * 2 * 2 * 3 * 11 * 11 * 11] /3
or
10648 = 2 * 2 * 2 * 11 * 11 * 11
∴ 10648 is a perfect cube.
Thus, the required least number = 3.

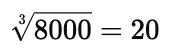


 Cube of a number
Cube of a number 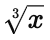 is the inverse operation of cubing x.
is the inverse operation of cubing x.