Model-Oriented Vs. Property-Oriented Approach
Formal methods are usually classified into two broad categories – model – oriented and property – oriented approaches. In a model-oriented style, one defines a system’s behaviour directly by constructing a model of the system in terms of mathematical structures such as tuples, relations, functions, sets, sequences, etc. In the property-oriented style, the system's behaviour is defined indirectly by stating its properties, usually in the form of a set of axioms that the system must satisfy.
Example
Let us consider a simple producer/consumer example. In a property-oriented style, we would probably start by listing the properties of the system like: the consumer can start consuming only after the producer has produced an item, the producer starts to produce an item only after the consumer has consumed the last item, etc. Examples of property-oriented specification styles are axiomatic specification and algebraic specification. In a modeloriented approach, we start by defining the basic operations, p (produce) and c (consume). Then we can state that S1 + p → S, S + c → S1. Thus the model-oriented approaches essentially specify a program by writing another, presumably simpler program. Examples of popular model-oriented specification techniques are Z, CSP, CCS, etc.
In the property-oriented style, the system's behaviour is defined indirectly by stating its properties, usually in the form of a set of axioms that the system must satisfy.
Model-oriented approaches are more suited to use in later phases of life cycle because here even minor changes to a specification may lead to drastic changes to the entire specification. They do not support logical conjunctions (AND) and disjunctions (OR). Property-oriented approaches are suitable for requirements specification because they can be easily changed. They specify a system as a conjunction of axioms and you can easily replace one axiom with another one.
Operational Semantics
Informally, the operational semantics of a formal method is the way computations are represented. There are different types of operational semantics according to what is meant by a single run of the system and how the runs are grouped together to describe the behaviour of the system. Some commonly used operational semantics are as follows:
Linear Semantics
In this approach, a run of a system is described by a sequence (possibly infinite) of events or states. The concurrent activities of the system are represented by non-deterministic inter-leavings of the automatic actions. For example, a concurrent activity a║b is represented by the set of sequential activities a;b and b;a. This is a simple but rather unnatural representation of concurrency. The behaviour of a system in this model consists of the set of all its runs. To make this model realistic, usually justice and fairness restrictions are imposed on computations to exclude the unwanted interleaving.
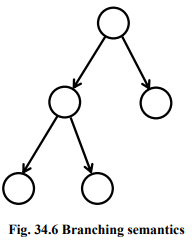
Branching Semantics
In this approach, the behaviour of a system is represented by a directed graph as shown in the fig. 34.6. The nodes of the graph represent the possible states in the evolution of a system. The descendants of each node of the graph represent the states which can be generated by any of the atomic actions enabled at that state. Although this semantic model distinguishes the branching points in a computation, still it represents concurrency by interleaving.
Maximally Parallel Semantics
In this approach, all the concurrent actions enabled at any state are assumed to be taken together. This is again not a natural model of concurrency since it implicitly assumes the availability of all the required computational resources.
Partial Order Semantics
Under this view, the semantics ascribed to a system is a structure of states satisfying a partial order relation among the states (events). The partial order represents a precedence ordering among events, and constrains some events to occur only after some other events have occurred; while the occurrence of other events (called concurrent events) is considered to be incomparable. This fact identifies concurrency as a phenomenon not translatable to any interleaved representation.
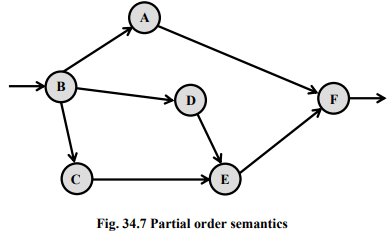
For example, Fig. 34.7 shows that we can compare node B with node D, but we can't compare node D with node A. A B C D E F Fig. 34.7 Partial order semantics
Merits of Formal Requirements Specification
Formal methods possess several positive features, some of which are discussed below.
• Formal specifications encourage rigour. Often, the very process of construction of a rigorous specification is more important than the formal specification itself. The construction of a rigorous specification clarifies several aspects of system behaviour that are not obvious in an informal specification.
• Formal methods usually have a well-founded mathematical basis. Thus, formal specifications are not only more precise, but also mathematically sound and can be used to reason about the properties of a specification and to rigorously prove that an implementation satisfies its specifications.
• Formal methods have well-defined semantics. Therefore, ambiguity in specifications is automatically avoided when one formally specifies a system.
• The mathematical basis of the formal methods facilitates automating the analysis of specifications. For example, a tableau-based technique has been used to automatically check the consistency of specifications. Also, automatic theorem proving techniques can be used to verify that an implementation satisfies its specifications. The possibility of automatic verification is one of the most important advantages of formal methods.
• Formal specifications can be executed to obtain immediate feedback on the features of the specified system. This concept of executable specifications is related to rapid prototyping. Informally, a prototype is a “toy” working model of a system that can provide immediate feedback on the behaviour of the specified system, and is especially useful in checking the completeness of specifications.
Limitations of Formal Requirements Specification
It is clear that formal methods provide mathematically sound frameworks using which systems can be specified, developed and verified in a systematic manner. However, formal methods suffer from several shortcomings, some of which are the following:
• Formal methods are difficult to learn and use.
• The basic incompleteness results of first-order logic suggest that it is impossible to check absolute correctness of systems using theorem proving techniques.
• Formal techniques are not able to handle complex problems. This shortcoming results from the fact that, even moderately complicated problems blow up the complexity of formal specification and their analysis. Also, a large unstructured set of mathematical formulae is difficult to comprehend.
Axiomatic Specification
In axiomatic specification of a system, first-order logic is used to write the pre and postconditions to specify the operations of the system in the form of axioms. The pre-conditions basically capture the conditions that must be satisfied before an operation can successfully be invoked. In essence, the pre-conditions capture the requirements on the input parameters of a function. The post-conditions are the conditions that must be satisfied when a function completes execution and the function is considered to have been executed successfully. Thus, the postconditions are essentially the constraints on the results produced for the function execution to be considered successful.
Steps to Develop an Axiomatic Specification
The following are the sequence of steps that can be followed to systematically develop the axiomatic specifications of a function:
• Establish the range of input values over which the function should behave correctly. Also find out other constraints on the input parameters and write them in the form of a predicate.
• Specify a predicate defining the conditions which must hold on the output of the function if it behaved properly.
• Establish the changes made to the function’s input parameters after execution of the function. Pure mathematical functions do not change their input and therefore this type of assertion is not necessary for pure functions.
• Combine all of the above into pre and post conditions of the function.
Examples
Example 1
Specify the pre- and post-conditions of a function that takes a real number as argument and returns half the input value if the input is less than or equal to 100, or else returns double the value.
f (x : real) : real
pre : x ∈ R
post : {(x≤100) ∧ (f(x) = x/2)} ∨ {(x>100) ∧ (f(x) = 2∗x)}
Example 2
Axiomatically specify a function named search which takes an integer array and an integer key value as its arguments and returns the index in the array where the key value is present.
search(X : IntArray, key : Integer) : Integer
pre : ∃ i ∈ [Xfirst….Xlast], X[i] = key
post : {(X′[search(X, key)] = key) ∧ (X = X′)}
Here, the convention that has been followed is that, if a function changes any of its input parameters, and if that parameter is named X, then it has been referred that after the function completes execution as X′.
Algebraic Specification
In the algebraic specification technique an object class or type is specified in terms of relationships existing between the operations defined on that type. It was first brought into prominence by Guttag [1980, 1985] in specification of abstract data types. Various notations of algebraic specifications have evolved, including those based on OBJ and Larch languages.
Representation of Algebraic Specification
Essentially, algebraic specifications define a system as a heterogeneous algebra. A heterogeneous algebra is a collection of different sets on which several operations are defined. Traditional algebras are homogeneous. A homogeneous algebra consists of a single set and several operations; {I, +, -, *, /}. In contrast, alphabetic strings together with operations of concatenation and length {A, I, con, len}, is not a homogeneous algebra, since the range of the length operation is the set of integers. To define a heterogeneous algebra, we first need to specify its signature, the involved operations, and their domains and ranges. Using algebraic specification, we define the meaning of a set of interface procedure by using equations. An algebraic specification is usually presented in four sections.
1. Types section
In this section, the sorts (or the data types) being used are specified.
2. Exceptions section
This section gives the names of the exceptional conditions that might occur when different operations are carried out. These exception conditions are used in the later sections of an algebraic specification.
3. Syntax section
This section defines the signatures of the interface procedures. The collection of sets that form input domain of an operator and the sort where the output is produced are called the signature of the operator. For example, PUSH takes a stack and an element and returns a new stack.
stack x element → stack
4. Equations section
This section gives a set of rewrite rules (or equations) defining the meaning of the interface procedures in terms of each other. In general, this section is allowed to contain conditional expressions.
Operators
By convention, each equation is implicitly universally quantified over all possible values of the variables. Names not mentioned in the syntax section such ‘r’ or ‘e’ are variables. The first step in defining an algebraic specification is to identify the set of required operations. After having identified the required operators, it is helpful to classify them as basic constructor operators, extra constructor operators, basic inspector operators, or extra inspection operators. The definition of these categories of operators is as follows:
1. Basic construction operators: These operators are used to create or modify entities of a type. The basic construction operators are essential to generate all possible element of the type being specified. For example, ‘create’ and ‘append’ are basic construction operators.
2. Extra construction operators: These are the construction operators other than the basic construction operators. For example, the operator ‘remove’ is an extra construction operator, because even without using ‘remove’ it is possible to generate all values of the type being specified.
3. Basic inspection operators: These operators evaluate attributes of a type without modifying them, e.g., eval, get, etc. Let S be the set of operators whose range is not the data type being specified. The set of the basic operators S1 is a subset of S, such that each operator from S-S1 can be expressed in terms of the operators from S1.
4. Extra inspection operators. These are the inspection operators that are not basic inspectors.
Writing Algebraic Specifications
A good rule of thumb while writing an algebraic specification, is to first establish which are the constructor (basic and extra) and inspection operators (basic and extra). Then write down an axiom for composition of each basic construction operator over each basic inspection operator and extra constructor operator. Also, write down an axiom for each of the extra inspector in terms of any of the basic inspectors. Thus, if there are m1 basic constructors, m2 extra constructors, n1 basic inspectors, and n2 extra inspectors, we should have m1 × (m2+n1) + n2 axioms are the minimum required and many more axioms may be needed to make the specification complete. Using a complete set of rewrite rules, it is possible to simplify an arbitrary sequence of operations on the interface procedures.
The first step in defining an algebraic specification is to identify the set of required operations. After having identified the required operators, it is helpful to classify them as basic constructor operators, extra constructor operators, basic inspector operators, or extra inspector operators. A simple way to determine whether an operator is a constructor (basic or extra) or an inspector (basic or extra) is to check the syntax expression for the operator. If the type being specified appears on the right hand side of the expression then it is a constructor, otherwise it is an inspection operator. For example, in case of the following example, create is a constructor because point appears on the right hand side of the expression and point is the data type being specified. But, xcoord is an inspection operator since it does not modify the point type.
Example
Let us specify a data type point supporting the operations create, xcoord, ycoord, and isequal where the operations have their usual meaning.
Types:
defines point
uses boolean, integer
Syntax:
create : integer × integer → point
xcoord : point → integer
ycoord : point → integer
isequal : point × point → Boolean
Equations:
xcoord(create(x, y)) = x
ycoord(create(x, y)) = y
isequal(create(x1, y1), create(x2, y2)) = ((x1 = x2) and (y1 = y2))
In this example, we have only one basic constructor (create), and three basic inspectors (xcoord, ycoord, and isequal). Therefore, we have only 3 equations.
Properties of Algebraic Specifications
Three important properties that every good algebraic specification should possess are:
Completeness: This property ensures that using the equations, it should be possible to reduce any arbitrary sequence of operations on the interface procedures. There is no simple procedure to ensure that an algebraic specification is complete.
Finite termination property: This property essentially addresses the following question: Do applications of the rewrite rules to arbitrary expressions involving the interface procedures always terminate? For arbitrary algebraic equations, convergence (finite termination) is undecidable. But, if the right hand side of each rewrite rule has fewer terms than the left, then the rewrite process must terminate.
Unique termination property: This property indicates whether application of rewrite rules in different orders always result in the same answer. Essentially, to determine this property, the answer to the following question needs to be checked: Can all possible sequence of choices in application of the rewrite rules to an arbitrary expression involving the interface procedures always give the same number? Checking the unique termination property is a very difficult problem.
Structured Specification
Developing algebraic specifications is time consuming. Therefore efforts have been made to device ways to ease the task of developing algebraic specifications. The following are some of the techniques that have successfully been used to reduce the effort in writing the specifications. Incremental specification: The idea behind incremental specification is to first develop the specifications of the simple types and then specify more complex types by using the specifications of the simple types. Specification instantiation: This involves taking an existing specification which has been developed using a generic parameter and instantiating it with some other sort.
Pros and Cons of Algebraic Specifications
Algebraic specifications have a strong mathematical basis and can be viewed as heterogeneous algebra. Therefore, they are unambiguous and precise. Using an algebraic specification, the effect of any arbitrary sequence of operations involving the interface procedures can automatically be studied. A major shortcoming of algebraic specifications is that they cannot deal with side effects. Therefore, algebraic specifications are difficult to interchange with typical programming languages. Also, algebraic specifications are hard to understand.
Executable Specification Language (4GL)
If the specification of a system is expressed formally or by using a programming language, then it becomes possible to directly execute the specification. However, executable specifications are usually slow and inefficient, 4GLs3 (4th Generation Languages) are examples of executable specification languages. 4GLs are successful because there is a lot of commonality across data processing applications. 4GLs rely on software reuse, where the common abstractions have been identified and parameterized. Careful experiments have shown that rewriting 4GL programs in higher level languages results in up to 50% lower memory usage and also the program execution time can reduce by ten folds. Example of a 4GL is Structured Query Language (SQL).





















