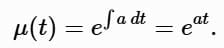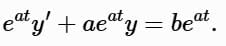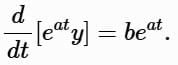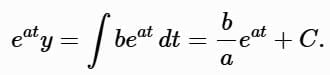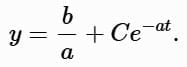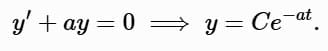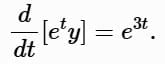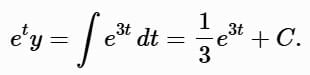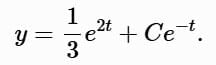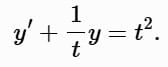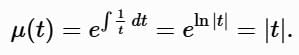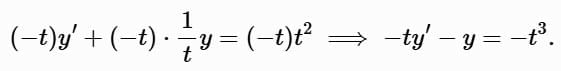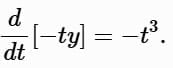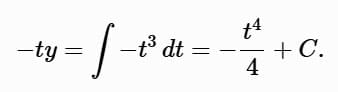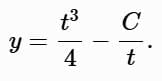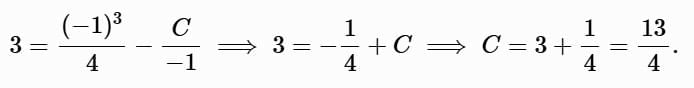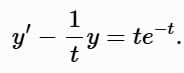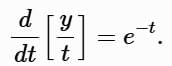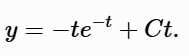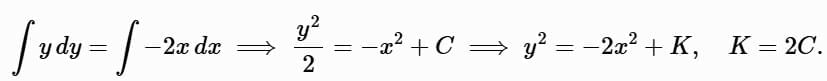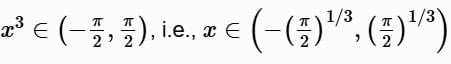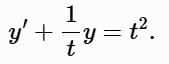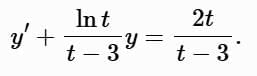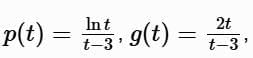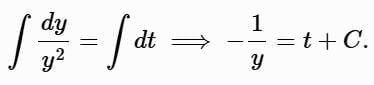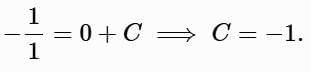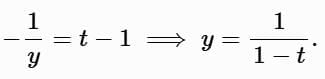Linear Ordinary Differential Equations of First and Second Order - 1 | Physics for IIT JAM, UGC - NET, CSIR NET PDF Download
First-order differential equations involve the first derivative of an unknown function y (t). They are of the form:
y′ = f(t, y),
where y′ = dy/dt, and f (t, y) is a given function. These notes cover two main types: linear and separable equations, with a focus on solution methods and exam-relevant techniques.
Linear First-Order Differential Equations
A linear first-order differential equation has the form:
y′ + p(t)y = g(t),
where p (t) and g (t) are functions of t. The solution method is the integrating factor technique.
Method of Integrating Factors
Multiply both sides of the equation by an integrating factor μ (t): μ(t)y′ + μ(t)p(t)y = μ(t)g(t).
Choose μ (t) such that the left-hand side is the derivative of a product: By the product rule, d/dt [μ (t) y] = μ (t) y ′ + μ ′ (t) y . Equate coefficients of y:
By the product rule, d/dt [μ (t) y] = μ (t) y ′ + μ ′ (t) y . Equate coefficients of y:
μ′(t)y = μ(t)p(t)y ⟹ μ′(t) = μ(t)p(t).
This simplifies to: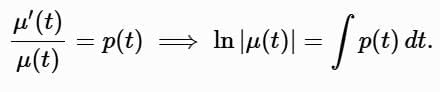 Thus, the integrating factor is:
Thus, the integrating factor is: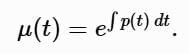 The constant of integration can be omitted, as any μ (t) of this form works. The equation becomes:
The constant of integration can be omitted, as any μ (t) of this form works. The equation becomes:
Integrate both sides: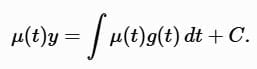
Solve for y: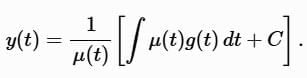
Examples
Example 1: Solve y ′ + ay = b , where a ≠ 0 , with no initial condition
Here, p (t) = a , g (t) = b. The integrating factor is:
Multiply through:
The left-hand side is:
Integrate:
Solve for y :
For the homogeneous case (b = 0 ):
The general solution combines the homogeneous and particular solutions, confirming the result.
Example 2: Solve y ′ + y = e2t
Here, p (t) = 1 , g (t) = e2t . The integrating factor is:
Multiply through:
The left-hand side is:
Integrate:
Solve for y:
Verify by substituting back to ensure correctness (a good exam practice).
Example 3: Solve ty ′ + y = t3, y ( − 1 ) = 3
Rewrite in standard form (t ≠ 0):
Here, p(t) = 1/t, g (t) = t2. The integrating factor is:
Since y (− 1) = 3 implies t < 0 , use μ (t) = − t for t < 0 . Multiply through:
The left-hand side is:
Integrate:
Solve for y:
Apply the initial condition y (− 1) = 3:
Thus:
The solution is valid for t < 0 , as t = 0 makes the denominator undefined.
Example 4: Solve t y ′ − y = t2e − t, t > 0
Rewrite in standard form:
Here, p(t) = -1/t, g (t) = te−t. The integrating factor is:
Multiply through:
The left-hand side is:
Integrate:
Solve for y :
No initial condition is provided, so this is the general solution for t > 0.
Separable Equations
A separable equation is of the form: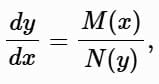
where M (x) and N (y) depend only on x and y , respectively.
Rewrite as: N(y)dy = M(x)dx.
Integrate both sides to find the solution, often implicitly:
Examples
Example 1: Solve y ′ = − 2x/y, y (π) = 2
Rewrite: y dy = −2x dx.
Integrate:Apply the initial condition y (π) = 2:
4 = −2π2 + K ⟹ K = 4 + 2π2.
Thus,
y2 = −2x2 + 4 + 2π2.
Solve explicitly:Since y (π) = 2, take the positive root. The solution is valid where − 2x2 + 4 + 2π2 > 0.
Example 2: Solve y ′ = 3x2(1 + y2) , y (0) = 0
Rewrite:
Integrate:
Apply the initial condition y (0) = 0:
arctan 0 = 0 + C ⟹ C = 0.
Thus:
arctan y = x3 ⟹ y = tan(x3).
The solution is defined where
Example 3: Solve 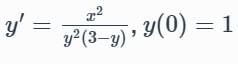
Rewrite: y2(3 − y)dy = x2dx.
Integrate: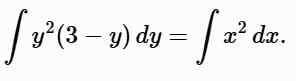 Left-hand side:
Left-hand side: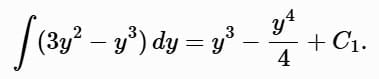 Right-hand side:
Right-hand side: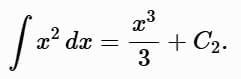
Thus: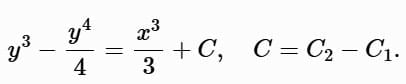
Apply the initial condition y (0) = 1: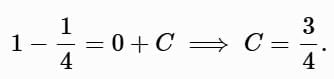 Thus:
Thus: To find the valid interval, note that y ′ is undefined at y = 0 or y = 3 . Check for x values:
To find the valid interval, note that y ′ is undefined at y = 0 or y = 3 . Check for x values:
At y = 0:
At y = 3: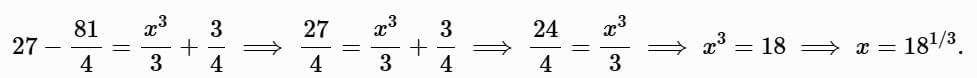
Since y (0) = 1 , the solution is valid between these points: − (9/4)1/3 < x < 181/3.
Existence and Uniqueness
For a linear equation y ′ + p (t) y = g (t), y (t0) = y0:
- If p (t) and g (t) are continuous on an open interval containing t0, the solution exists and is unique on that interval.
For a nonlinear equation y′ = f(t, y), y (t0) = y0:
- If f and ∂f/∂y are continuous in a rectangle around (t0, y0), a unique solution exists in some interval around t0.
Examples
Example 1: Largest interval for ty′ + y = t3, y (− 1) = 3
Standard form:
Here, p (t) = 1/t , g (t) = t2, undefined at t = 0 . Since t0 = − 1 , the solution is valid for t < 0.
Example 2: Largest interval for (t − 3) y ′+ (ln t) y = 2 t , y (1) = 2
Standard form:
Here,
undefined at t = 0 (due to ln t ) and t = 3. Since t0 = 1 , the interval is 0 < t < 3.
Example 3: Blow-up for y ′ = y2, y ( 0 ) = 1
Separate variables:
Apply y(0) = 1:
Thus:
The solution blows up at t = 1 , undefined beyond this point.
FAQs on Linear Ordinary Differential Equations of First and Second Order - 1 - Physics for IIT JAM, UGC - NET, CSIR NET
| 1. What is a linear ordinary differential equation of first order? |  |
| 2. How do you solve a linear ordinary differential equation of first order? |  |
| 3. What is a linear ordinary differential equation of second order? |  |
| 4. Can linear ordinary differential equations of second order have non-constant coefficients? |  |
| 5. What are the applications of linear ordinary differential equations in physics? |  |