Introduction: Cubes & Cuboids | CAT Preparation Course for Working Professionals PDF Download
Introduction
- In a cube or a cuboid, there are six faces in each.
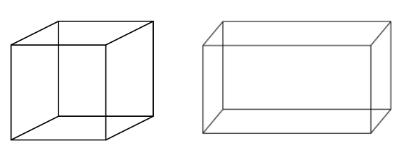 Cube & Cuboid
Cube & Cuboid - In a cube length, breadth and height are the same while in a cuboid these are different.
- In a cube the number of unit cubes = (side)3.
- In cuboid the number of unit cube = (l x b x h).
Basic Structure of a Cube
A cube is a 3-dimensional structure with three sides (length, width, and height) where all the sides equal (length = width= height).
The word cube is derived from the Arabic word ”Kaba” a large cube-shaped structure.
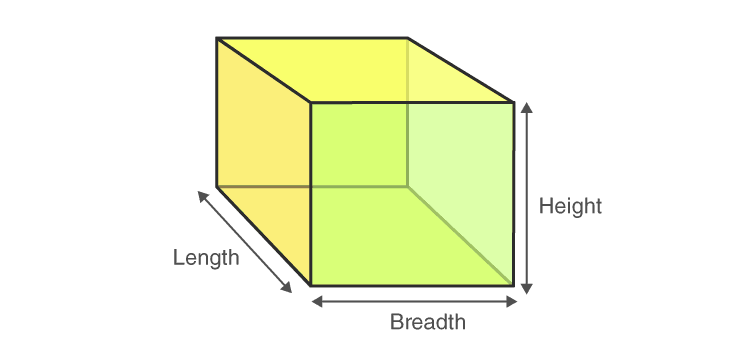
- A cube has 6 faces: The faces appear at front, back, right, left, top and bottom.
- Cube has 8 vertices: The corner points are called vertices. There are four vertices on the top face and four more at the bottom face.
- Cube has 12 Edges: The line which connects the two vertices is called edges. There are twelve edges in a cube. Four on the top surface and four at the bottom and four more verticle lines connecting the opposite vertices of top and bottom face.

Net of a Cube
- The net of a solid is a diagram drawn on paper which when cut and folded along the lines can be used to construct a solid shape.
- Net of a Cube is a two-dimensional shape that can be folded into a three dimensional figure is a Cube.
- A Cube consists of 6 square faces, 12 edges, and 8 vertices.
- When the square faces of a cube are separated at the edges and laid out flat, they make a two-dimensional figure called a net.
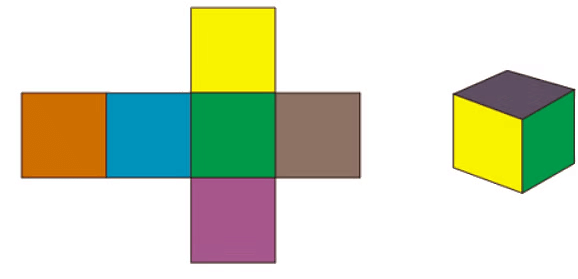
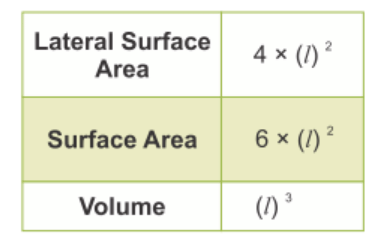
Formulas of a Cube
1. Lateral Surface Area of a Cube:
Consider a Cube of edge length ‘a′ , then, the area of each face of a square = a2
So, the Lateral Surface Area of a Cube = Sum of the area of all 4 side faces Lateral Surface Area(LSA) = 4a2 square units
2. Total Surface of a Cube
We know the cube consists of 6 square faces. Let us consider if each side of a cube is a , then the total surface area of the Cube is = 6a2.
Total Surface Area (TSA) = 6a2 square units
3. Volume of a Cube
The volume of a cube can be found by multiplying the edge length three times. If each edge length is “a” , then the Volume of a Cube is a3.
V = a3 cubic units
Visualising the Opening and Closing of Cubes
The accompanying figures represent open cubes, and the accompanying text specifies which faces would align opposite each other when the cube is folded into a closed box.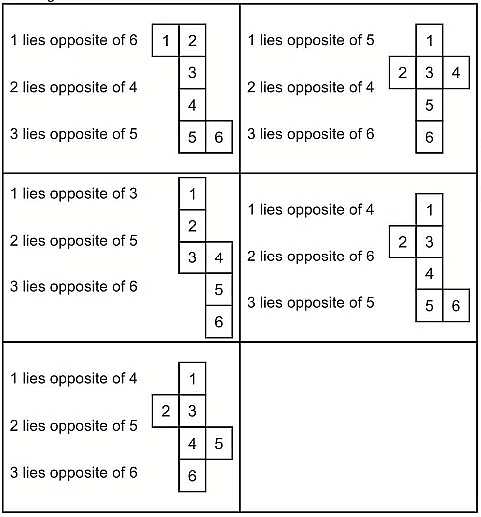
Painting and Cutting a cube
When confronted with the task of visualizing the distribution of painted faces on a cube after making cuts along its axes, specific formulae come in handy. Although it is beneficial to memorize these formulae, it is equally important to develop the ability to mentally picture these outcomes when faced with a real problem.1. Cutting equidistant along each axis with an equal number of cuts
Consider a cube painted black, and if we make n cuts along each axis, the distribution of smaller cubes with varying numbers of painted faces can be determined using specific formulas:Number of cubes with 3 faces painted black: 8 (corresponding to all corner cubes).
Number of cubes with 2 faces painted black: (n - 1) × 12.
Number of cubes with 1 face painted black: (n - 1)² × 6.
Number of cubes with no face painted black: (n - 1)³.
For instance, if we make two equidistant cuts on each edge of the cube (n = 2), we would obtain 27 smaller cubes. Out of these 27 cubes, 8 would have three sides painted black, 12 would have two sides painted black ((n - 1) × 12 = (2 - 1) × 12 = 12), 6 would have one side painted black ((n - 1)² × 6 = (2 - 1)² × 6 = 6), and 1 cube would have no sides painted ((n - 1)³ = (2 - 1)³ = 1).
For n = 3, resulting in 64 smaller cubes, the distribution would be as follows:
Cubes with 3 sides painted: 8.
Cubes with 2 sides painted: (n - 1) × 12 = (3 - 1) × 12 = 24.
Cubes with 1 side painted: (n - 1)² × 6 = 24.
Cubes with no side painted: (n - 1)³ = (3 - 1)³ = 8.
Visualizing these cases aids in better understanding and mastery of the problem.
2. Cutting equidistant along each axis with an unequal number of cuts
In scenarios where the number of cuts differs, for instance, "a" cuts on the X-axis, "b" cuts on the Y-axis, and 'c' cuts on the Z-axis, the resulting smaller pieces are not cubes but cuboids. Consequently, questions may inquire about determining the number of cuboids with specific painted face configurations.
Number of cuboids with 3 faces painted: Consists of all corner cuboids, totaling 8 cuboids.
Number of cuboids with exactly 2 faces painted: (a - 2) × 4 + (b - 2) × 4 + (c - 2) × 4.
Number of cuboids with exactly 1 face painted: 2 × [(a - 2)(b - 2) + (b - 2)(c - 2) + (a - 2)(c - 2)].
Number of cuboids with 0 faces painted: Corresponds to the inner cuboid and equals (a - 2) × (b - 2) × (c - 2).
It's important to visualize a scenario where the faces of the cuboids are not uniformly painted but have different colors, with each color used to paint two faces.
Basic Structure of a Cuboid
A cuboid is also a polyhedron having six faces, eight vertices and twelve edges. The faces of the cuboid are parallel. But not all the faces of a cuboid are equal in dimensions.
A cuboid is a closed 3-dimensional geometrical figure bounded by six rectangular plane regions.
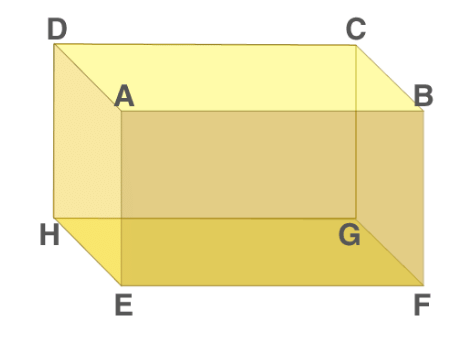 Cuboid Shape
Cuboid Shape
Properties of a Cuboid
Below are the properties of cuboid, its faces, base and lateral faces, edges and vertices.
1. Faces of Cuboid
- A Cuboid is made up of six rectangles, each of the rectangles is called the face. In the figure above, ABFE, DAEH, DCGH, CBFG, ABCD and EFGH are the 6 faces of cuboid.
- The top face ABCD and bottom face EFGH form a pair of opposite faces. Similarly, ABFE, DCGH, and DAEH, CBFG are pairs of opposite faces. Any two faces other than the opposite faces are called adjacent faces.
- Consider a face ABCD, the adjacent face to this are ABFE, BCGF, CDHG, and ADHE.
2. Base and lateral faces
- Any face of a cuboid may be called the base of the cuboid. The four faces which are adjacent to the base are called the lateral faces of the cuboid. Usually, the surface on which a solid rests on is known to be the base of the solid.
In Figure above, EFGH represents the base of a cuboid.
3. Edges
- The edge of the cuboid is a line segment between any two adjacent vertices.
- There are 12 edges, they are AB, AD, AE, HD, HE, HG, GF, GC, FE, FB, EF and CD and the opposite sides of a rectangle are equal.
- Hence, AB = CD = GH = EF, AE = DH = BF = CG and EH = FG = AD = BC.
4. Vertices of Cuboid
- The point of intersection of the 3 edges of a cuboid is called the vertex of a cuboid.
- A cuboid has 8 vertices A, B, C, D, E, F, G and H represents vertices of the cuboid in fig 1.
- By observation, the twelve edges of a cuboid can be grouped into three groups, such that all edges in one group are equal in length, so there are three distinct groups and the groups are named as length, breadth and height.
- A solid having its length, breadth, height all to be equal in measurement is called a cube. A cube is a solid bounded by six square plane regions, where the side of the cube is called edge.
Net of a Cuboid
- A cuboid consists of 6 rectangular faces, 12 edges, and 8 vertices.
- When the rectangular faces of a cuboid are separated at the edges and laid out flat, they make a two-dimensional figure called a net of a Cuboid.
- A cuboid shape is like that of a rectangular shoe box.
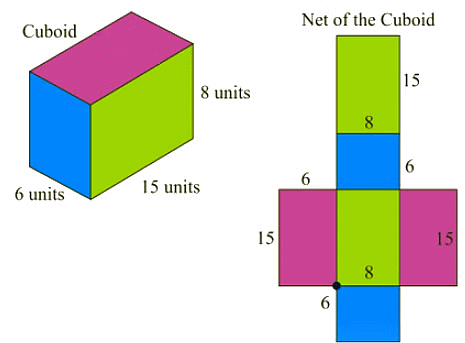
Formulas of a Cuboid
1. Lateral Surface Area of a Cuboid
- Lateral Surface Area of a cuboid = Sum of four vertical sides
- Lateral Surface Area (LSA) = 2h(l + b) square units
2. Total Surface of a Cuboid
We know the cuboid consists of 6 rectangular faces.
Total Surface Area (TSA) =2(lb+bh+hl) square units
Where, l= length, b= breadth, h= height
3. Volume of a Cuboid
Volume of a cuboid is V = length × breadth × height
V = (l × b × h) Cubic units
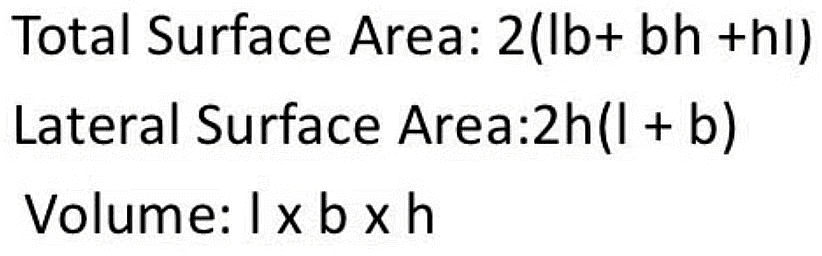
Difference Between Cube and Cuboid
- The sides of the cube are equal but for cuboid they are different.
- The sides of the cube are square in shape but for cuboid, they are in a rectangular shape.
- All the diagonals of the cube are equal but a cuboid has equal diagonals for only parallel sides.
Cube and Cuboid Formulas
Table: The formulas for cube and cuboid are defined based on their surface areas, lateral surface areas and volume.
Tips and Tricks to Solve Questions Based on Cube and Dice
Candidates can find various tips and tricks from below for solving the questions related to the Cube and Dice reasoning section.- Tip # 1: In a cube we find Length = width = height. Altogether there are six surfaces, twelve edges and eight corners
- Tip # 2: Cuboid = in a cuboid length and breadth is not as same as its height.
- Tip # 3: Types of dice are Ordinary Dice and Standard Dice
- Tip # 4: It is a regular cube with its six sides numbered with dots from 1 to 6 with opposite sides adding up to 7.
- Tip # 5: In standard dice, always “6 is opposite to 1”, “5 is opposite to 2” and “4 is opposite to 3”.
- Tip # 6: In ordinary dice, Sum of any two number of the adjacent surface is = 7
Solved Questions
Q1: Observe the cube shown. It has been divided into ¼ of its original side length. Hence the total number of smaller or unit cubes formed will be 64.
(a) How many unit cubes have only three sides painted?

Solution: The cubes with three of their sides painted lie at the vertices of the cubes (The cubes coloured in red). There are eight such cubes. Hence the answer is eight.
(b) How many cubes have only two sides painted?
Solution: The cubes with two sides painted lie at the edges (the cubes coloured in blue). Evaluate such cubes for one tip and multiply the result by 12. (as there are 12 edges in a cube). From the figure, it is clear that there are two blue cubes at an edge. Hence the total number of such cubes will be 2*12 = 24.
Alternate solution:
The value of n for the given cube 4. Substituting it in the formula we get 12 x(4-2) = 24.
(c) How many cubes have only one side painted?
Solution: The cubes with only one side painted always lie at the surface. Evaluate the number of such faces at each surface and multiply the result by six. As there are six faces in a cube. From the figure, it is clear that there are four white cubes at the surface. Hence the total number of such cubes will be 6*4 = 24.
(d) How many cubes have no side painted?
Solution: The cubes at the inner core part of the cube will not have any side painted. Evaluating it every time for different cubes is a tedious task. The simple and easiest approach is by analyzing the pattern.
In 2*2*2 cube there are zero cubes that have no side painted. Whereas in 3*3*3 cube there is only one cube at the core part which has no sides painted.
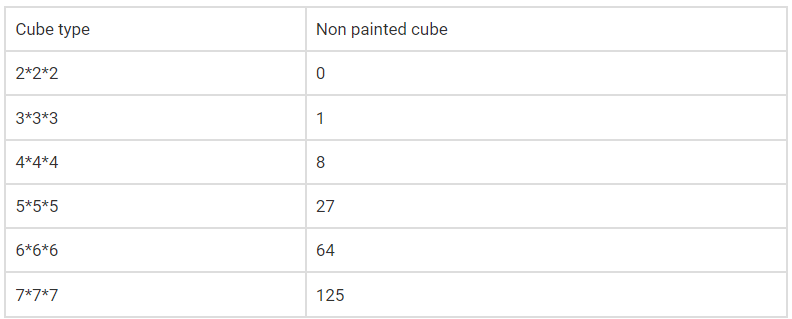
The logical pattern from the table follows that the total number of cubes with no side painted will always be equal to the cube of natural numbers.
Q2: Directions: A cube of side 10 cm is coloured red with a 2 cm wide green strip along all the sides on all the faces. The cube is divided into 125 smaller cubes of equal size. Answer the following questions based on this statement.
- How many cubes have three green faces each?
- How many cubes have one face red and an adjacent face green?
- How many cubes have at least one face coloured?
- How many cubes have at least two green faces each?
Solution:
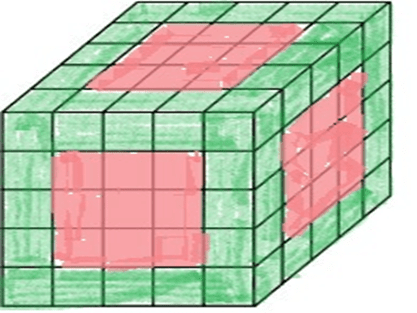
- All the corner cubes are painted green. So there are 8 cubes with 3 sides painted green.
- There is no cube having one face red and an adjacent face green as all the green painted cubes got paint on at least 2 faces.
- Let us calculate the number of cubes with no painting. By formula, = = 27
Therefore, there are 125 – 27 = 98 cubes having at least one face coloured.
- From the total cubes, Let us subtract the cubes with red painting, cubes with no painting.125 – (9 x 6) – 27 = 44
Q3: Directions: One hundred and twenty-five cubes of the same size are arranged in the form of a cube on a table. Then a column of five cubes is removed from each of the four corners. All the exposed faces of the rest of the solid (except the face touching the table) are coloured red. Now, answer these questions based on the above statement:
- How many small cubes are there in the solid after the removal of the columns?
- How many cubes do not have any coloured face?
- How many cubes have only one red face each?
- How many cubes have two coloured faces each?
- How many cubes have more than 3 coloured faces each?
Solution:
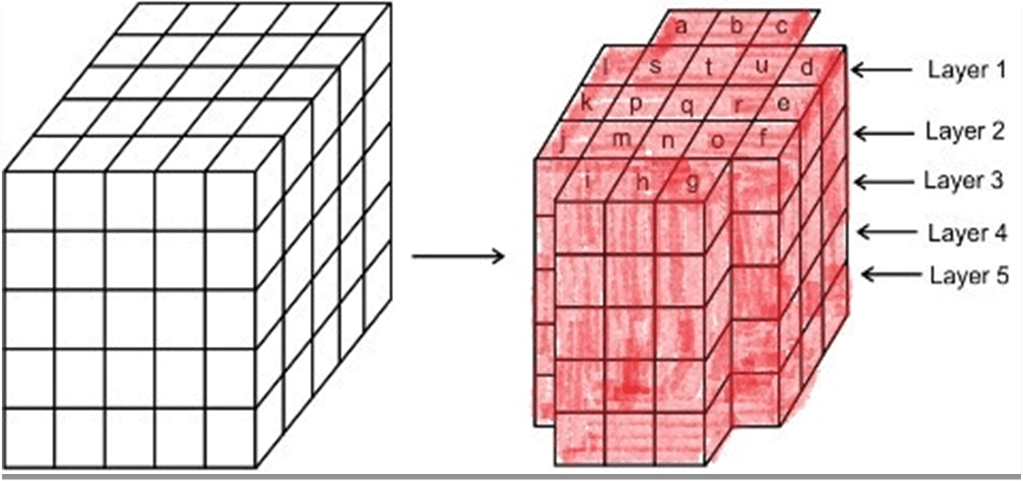
- Since out of 125 total number of cubes, we removed 4 columns of 5 cubes each, the remaining number of cubes = 125 – (4 x 5) = 125 – 20 = 105.
- Cubes with no paintings lie in the middle. So cubes which are below the cubes named as s, t, u, p, q, r, m, n, o got no painting. Since there are 4 rows below the top layer, total cubes with no painting are (9 x 4) = 36.
- There are 9 cubes named m, n, o, p, q, r, s, t, and u in layer 1, and 4 cubes (in columns b, e, h, and k) in each of layers 2, 3, 4 and 5 got one red face. Thus, there are 9 + (4 x 4) = 25 cubes.
- The columns (a, c, d, f, g, i, j, l) each got 4 cubes in layers 2, 3, 4, 5. Also in layer 1, h, k, b, e cubes got 2 faces coloured. so total cubes are 32 + 4 = 36
- There is no cube in the block having more than three coloured faces. There are 8 cubes (in the columns a, c, d, f, g, i, j and l) in layer 1 which have 3 coloured faces. Thus, there are 8 such cubes

Q4: A cube of each side 4 cm, has been painted black, red, and green on pairs of opposite faces. It is then cut into small cubes of each side 1 cm.
The following questions and answers are based on the information given above:
(a) How many small cubes will be there?
- Total no. of cubes = (sides)3 = (4)3 = 64
(b) How many small cubes will have three faces painted?
- From the figure, it is clear that the small cube having three faces coloured are situated at the corners of the big cube because at these corners only three faces of the big cube meet. Therefore the required number of such cubes is always 8 because there are 8 corners.
(c) How many small cubes will have only two faces painted?
- From the figure, it is clear that to each edge of the big cube 4 small cubes are connected and two out of them are situated at the corners of the big cube which have all three faces painted.
- Thus, to edge two small cubes are left which have two faces painted. As the total no. of edges in a cube are 12.
- Hence the no. of small cubes with two faces coloured = 12 x 2 = 24
(or)
No. of small cubes with two faces coloured = (x - 2) x No. of edges
where x = (side of big cube / side of small cube)
(d) How many small cubes will have only one face painted?
- The cubes which are painted on one face only are the cubes at the centre of each face of the big cube.
- Since there are 6 faces in the big cube and each of the face of the big cube there will be four small cubes.
- Hence, in all there will be 6 x 4 = 24 such small cubes (or) (x - 2)2 x 6.
(e) How many small cubes will have only two faces painted in black and green and all other faces unpainted?
- There are 4 small cubes in layer II and 4 small cubes in layer III which have two faces painted green and black.
- Required no. of such small cubes = 4 + 4 = 8.
(f) How many small cubes will have only two faces painted green and red?
- No. of small cubes having two faces painted green and red = 4 + 4 = 8.
(g) How many small cubes will have only two faces painted black and red?
- No. of small cubes having two faces painted black and red = 4 + 4 = 8.
(h) How many small cubes will have only black painted?
- No. of small cubes having only black paint. There will be 8 small cubes which have only black paint. Four cubes will be from one side and 4 from the opposite side.
(i) How many small cubes will be only red-painted?
- No. of small cubes having only red paint = 4 + 4 = 8.
(j) How many small cubes will be only green painted?
- No. of small cubes having only green paint = 4 + 4 = 8.
Q5: What number will be opposite to 2?
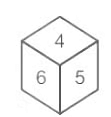
Solution: It is a standard dice as no of any adjacent sides are 7. As, standard dice, opposite no. of 2 will be
6 ↔ 1
5 ↔ 2
4 ↔ 3
Ans is 5, (sum of opposite side is 7)
Q6: What no will be opposite to 4?
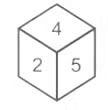
Solution: It is an ordinary dice as the sum of right and left side is 7. So, opposite no. of 4 can be – 1, 3 or 6.
So, the answer is → can’t be determined.
Q7: What no will be opposite to 3?
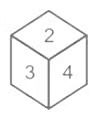
Solution: We have to check the possibility.
Here, the no of dice is1, 2, 3, 4, 5, 6 As per above diagram 3, 2 and 4. Can’t be any of the opposite faces of 2.
So, there are all eliminated only 1, 5 or 6 are possible numbers of opposite faces of 3.
Then option b is correct i.e. 1/5/6.
Q8: What is the example of a standard dice?
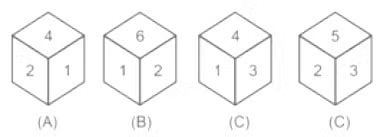
Solution: As per the definition of standard dice, any of the two opposite faces of dice must be 7.
So, only in dice A the sum of two adjacent faces is 7.
Hence, the correct answer is A.
|
303 videos|487 docs|279 tests
|
FAQs on Introduction: Cubes & Cuboids - CAT Preparation Course for Working Professionals
| 1. What is the basic structure of a cube? |  |
| 2. How can you visualize the opening and closing of cubes? |  |
| 3. What are the formulas related to a cube? |  |
| 4. How can you paint and cut a cube to understand its structure better? |  |
| 5. What are some tips and tricks to solve questions based on cubes and dice? |  |






















