Numerical Solutions of Algebraic Equations - CSIR-NET Mathematical Sciences | Mathematics for IIT JAM, GATE, CSIR NET, UGC NET PDF Download
NUMERICAL SOLUTIONS OF ALGEBRAIC AND TRANSCENDENTAL EQUATIONS
Aim: To find a root of f(x) = 0
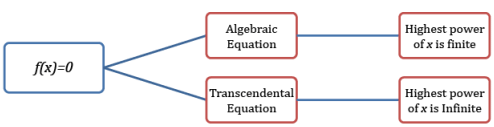
Algebraic Equation: An Equation which contains algebraic terms is called as an algebraic Equation.
Example: x2 + x + 1 = 0, Here Highest power of x is finite. So it is an algebraic Equation.
Transcendental Equation: An equation which contains trigonometric ratios, exponential function and logarithmic functions is called as a Transcendental Equation.
Example: ex + 2 = 0, sinx + 1 = 0, log(l + x) = 0 etc.
- Directive Methods: The methods which are used to find solutions of given equations in the direct process is called as directive methods.
Example: Synthetic division, remainder theorem, Factorization method etc
Note: By using Directive Methods, it is possible to find exact solutions of the given equation.
- Iterative Methods (Indirect Methods): The methods which are used to find solutions of the given equation in some indirect process is called as Iterative Methods
Note: By using Iterative methods, it is possible to find approximate solution of the given equation and also it is possible to find single solution of the given equation at the same time.
To find a root of the given equation, we have following methods
- Bisection Method
- The Method of false position (Or) Regular folsi Method
- Iteration Method (Successive approximation Method)
- Newton Raphson Method.
Bisection Method
Consider f(x) = 0 be the given equation.
Let us choose the constants and in such a way that 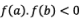
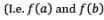 are of opposite signs) i.e.
are of opposite signs) i.e. 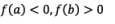
(or)
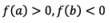
Then the curve y = f(x) crosses - in between a and b, so that there exists a root of the given equation in between a and b.
Let us define initial approximation 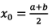
Now, If 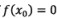 then x0 is root of the given equation.
then x0 is root of the given equation.
If f(x0) = ≠ 0 then either f(x0) < 0 (or) f(x0) > 0
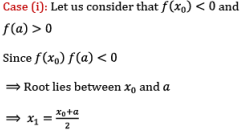
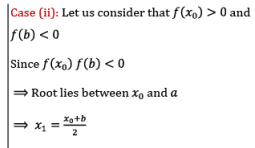
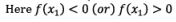
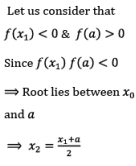



Here, the logic is that, we have to select first negative or first positive from bottom approximations only, but not from top. i.e. the approximation which we have recently found should be selected.
If f(x1) = 0, then x1 is root of the given equation. Otherwise repeat above process until we obtain solution of the given equation.
Regular Folsi Method (Or) Method of False position
Let us consider that y = f(x) be the given equation.
Let us choose two points a and b in such a way that f(a) and f(b) are of opposite signs. i.e. f(x0).f(x1) < 0
Consider f(a) > 0,f(b) < 0, so that the graph y = f(x) crosses .Y-axis in between a and b. then, there exists a root of the given equation in between a and b.
Let us define a straight line joining the points A(a,f(a)), B(b,f(b)) , then the equation of straight line is given by 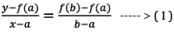
This method consists of replacing the part of the curve by means of a straight line and then takes the point of intersection of the straight line with -axis, which give an approximation to the required root.
In the present case, it can be obtained by substituting in equation I, and it is denoted by x0.
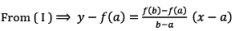
Now, any point on .Y-axis ⇒ y = 0 and let initial approximation be x0 i.e. x = x0
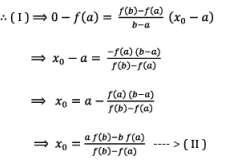
If f(x0) = 0 , then x0 is root of the given equation.
If fix0) ≠ 0 , then either f(x0) < 0 (or) f(x0) > 0
Case (i): Let us consider that f(x0) < 0
We know that f(a) > 0 and f(x0) < 0
Hence root of the given equation lies between a and x0.
In order to obtain next approximation x1, replace b with x0 in equation (II)
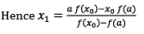
Case (ii): Let us consider that f(x0) > 0
We know that f(b) < 0 and f(x0) > 0
Hence root of the given equation lies between b and x0.
In order to obtain next approximation x1, replace a with x0 in equation (II)
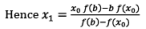
If f(x1) = 0, then x1 is root of the given equation. Otherwise repeat above process until we obtain a root of the given equation to the desired accuracy.
Newton Raphson Method
Let us consider that f(x) = 0 be the given equation.
Let us choose initial approximation to be x0.
Let us assume that x1 = x0 + h be exact root of f(x) = 0 where h << 0, so that f(x0 + h) = 0
Expanding above relation by means of Taylor's expansion method, we get
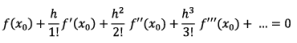
Since is h very small, h and higher powers of h are neglected. Then the above relation becomes
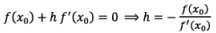
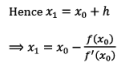
If f(x1)= 0, then is x1 root of the given equation. Otherwise repeat above process until we obtain a root of the given equation to the desired accuracy.
Successive approximations are given by
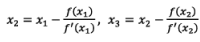
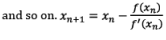
Iteration Method
Let us consider that f(x) = 0 be the given equation.
Let us choose initial approximation to be x0.
Rewrite f(x) = 0 as x = φ(x) such that |φ'(x0)| < 0.
Then successive approximations are given by
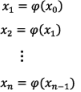
Repeat the above process until we get successive approximation equal, which will gives the required root of the given equation.
|
556 videos|198 docs
|
FAQs on Numerical Solutions of Algebraic Equations - CSIR-NET Mathematical Sciences - Mathematics for IIT JAM, GATE, CSIR NET, UGC NET
| 1. What is the numerical solution of an algebraic equation? |  |
| 2. What are some commonly used numerical methods for solving algebraic equations? |  |
| 3. How does the Newton-Raphson method work for solving algebraic equations? |  |
| 4. What is the bisection method for solving algebraic equations? |  |
| 5. Are there any limitations to numerical methods for solving algebraic equations? |  |
















