Numerical Solutions of ODEs using Picard Method - Numerical Analysis, CSIR-NET Mathematical Sciences | Mathematics for IIT JAM, GATE, CSIR NET, UGC NET PDF Download
NUMERICAL SOLUTION OF ORDINARY DIFFERENTIAL EQUATIONS (B)
PICARD’S METHOD
This method of solving a differential equation approximately is one of successive approximation; that is, it is an iterative method in which the numerical results become more and more accurate, the more times it is used.
An approximate value of y (taken, at first, to be a constant) is substituted into the right hand side of the differential equation
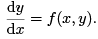
The equation is then integrated with respect to x giving y in terms of x as a second approximation, into which given numerical values are substituted and the result rounded off to an assigned number of decimal places or significant figures.
The iterative process is continued until two consecutive numerical solutions are the same when rounded off to the required number of decimal places.
A hint on notation
Imagine, for example, that we wished to solve the differential equation
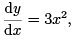
given that y = y0 = 7 when x = x0 = 2.
This ofcourse can be solved exactly to give
y = x3 + C,
which requires that
7 = 23 + C.
Hence,
y − 7 = x3 − 23;
or, in more general terms
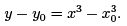
Thus,
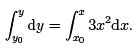
In other words,
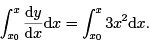
The rule, in future, therefore, will be to integrate both sides of the given differential equation with respect to x, from x0 to x.
EXAMPLES
1. Given that
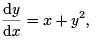
and that y = 0 when x = 0, determine the value of y when x = 0.3, correct to four places of decimals.
Solution
To begin the solution, we proceed as follows:
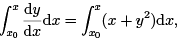
where x0 = 0.
Hence,
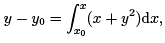
where y0 = 0.
That is,
(a) First Iteration
We do not know y in terms of x yet, so we replace y by the constant value y0 in the function to be integrated.
The result of the first iteration is thus given, at x = 0.3, by
(b) Second Iteration
Now we use
Therefore,
which gives
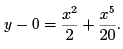
The result of the second iteration is thus given by
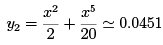
at x = 0.3.
(c) Third Iteration
Now we use
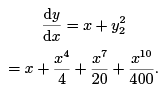
Therefore,
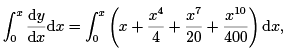
which gives
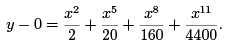
The result of the third iteration is thus given by

Hence, y = 0.0451, correct to four decimal places, at x = 0.3.
2. If
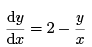
and y = 2 when x = 1, perform three iterations of Picard’s method to estimate a value for y when x = 1.2. Work to four places of decimals throughout and state how accurate is the result of the third iteration.
Solution
(a) First Iteration
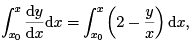
where x0 = 1.
That is,
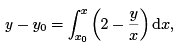
where y0 = 2.
Hence,
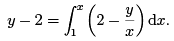
Replacing y by y0 = 2 in the function being integrated, we have
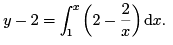
Therefore,
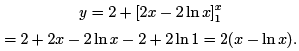
The result of the first iteration is thus given by
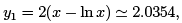
when x = 1.2.
(b) Second Iteration
In this case we use
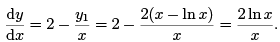
Hence,
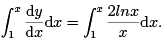
That is,
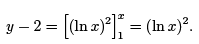
The result of the second iteration is thus given by
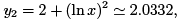
when x = 1.2.
(c) Third Iteration
Finally, we use
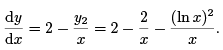
Hence,
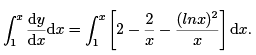
That is,
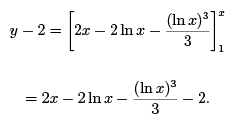
The result of the third iteration is thus given by
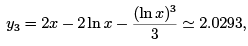
when x = 1.2.
The results of the last two iterations are identical when rounded off to two places of decimals, namely 2.03. Hence, the accuracy of the third iteration is two decimal place accuracy.
|
558 videos|198 docs
|
FAQs on Numerical Solutions of ODEs using Picard Method - Numerical Analysis, CSIR-NET Mathematical Sciences - Mathematics for IIT JAM, GATE, CSIR NET, UGC NET
| 1. What is the Picard method for solving ODEs? |  |
| 2. How does the Picard method work in solving ODEs? |  |
| 3. What are the advantages of using the Picard method for solving ODEs? |  |
| 4. Are there any limitations or drawbacks of using the Picard method for solving ODEs? |  |
| 5. Can the Picard method be used for solving partial differential equations (PDEs)? |  |

















