NCERT Solutions for Class 10 Maths Chapter 1 - Real Numbers (Exercise 1.4)
Q.1. Without actually performing the long division, state whether the following rational numbers will have a terminating decimal expansion or a non-terminating repeating decimal expansion:
(i) 13/3125
(ii) 17/8
(iii) 64/455
(iv) 15/1600
(v) 29/343
(vi) 23/(2352)
(vii) 129/(225775)
(viii) 6/15
(ix) 35/50
(x) 77/210
Solutions:
Note: If the denominator has only factors of 2 and 5 or in the form of 2m × 5n then it has terminating decimal expansion.
If the denominator has factors other than 2 and 5 then it has a non-terminating decimal expansion.
(i) 13/3125
Factorizing the denominator, we get,
3125 = 5 × 5 × 5 = 55
Since, the denominator has only 5 as its factor, 13/3125 has a terminating decimal expansion.
(ii) 17/8
Factorizing the denominator, we get,
8 = 2 × 2 × 2 = 23
Since, the denominator has only 2 as its factor, 17/8 has a terminating decimal expansion.
(iii) 64/455
Factorizing the denominator, we get,
455 = 5 × 7 × 13
Since, the denominator is not in the form of 2m × 5n, thus 64/455 has a non-terminating decimal expansion.
(iv) 15/ 1600
Factorizing the denominator, we get,
1600 = 2652
Since, the denominator is in the form of 2m × 5n, thus 15/1600 has a terminating decimal expansion.
(v) 29/343
Factorizing the denominator, we get,
343 = 7 × 7 × 7 = 73 Since, the denominator is not in the form of 2m × 5n thus 29/343 has a non-terminating decimal expansion.
(vi) 23/(2352)
Clearly, the denominator is in the form of 2m × 5n.
Hence, 23/ (2352) has a terminating decimal expansion.
(vii) 129/(225775)
As you can see, the denominator is not in the form of 2m × 5n.
Hence, 129/ (225775) has a non-terminating decimal expansion.
(viii) 6/15
6/15 = 2/5
Since, the denominator has only 5 as its factor, thus, 6/15 has a terminating decimal expansion.
(ix) 35/50
35/50 = 7/10
Factorising the denominator, we get,
10 = 2 5
Since, the denominator is in the form of 2m × 5n thus, 35/50 has a terminating decimal expansion.
(x) 77/210
77/210 = (7× 11)/ (30 × 7) = 11/30
Factorising the denominator, we get,
30 = 2 × 3 × 5
As you can see, the denominator is not in the form of 2m × 5n .Hence, 77/210 has a non-terminating decimal expansion.
Q.2. Write down the decimal expansions of those rational numbers in Question 1 above which have terminating decimal expansions.
Solutions:
(i) 13/3125
13/3125 = 0.00416
(ii) 17/8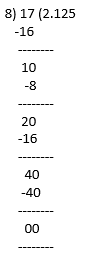
17/8 = 2.125
(iii) 64/455 has a Non terminating decimal expansion
(iv)15/ 1600
15/1600 = 0.009375
(v) 29/ 343 has a Non terminating decimal expansion
(vi)23/ (2352) = 23/(8×25)= 23/200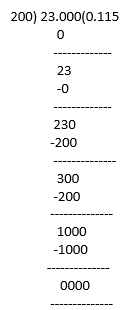
23/ (2352) = 0.115
(vii) 129/ (225775) has a Non terminating decimal expansion
(viii) 6/15 = 2/5 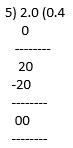
(ix) 35/50 = 7/10 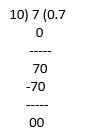
35/50 = 0.7
(x) 77/210 has a non-terminating decimal expansion.
Q.3. The following real numbers have decimal expansions as given below. In each case, decide whether they are rational or not. If they are rational, and of the form, p q what can you say about the prime factors of q?
(i) 43.123456789
(ii) 0.120120012000120000. . .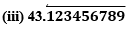
Solutions:
(i) 43.123456789
Since it has a terminating decimal expansion, it is a rational number in the form of p/q and q has factors of 2 and 5 only.
(ii) 0.120120012000120000. . .
Since, it has non-terminating and non- repeating decimal expansion, it is an irrational number.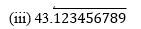
Since it has non-terminating but repeating decimal expansion, it is a rational number in the form of p/q and q has factors other than 2 and 5.
|
70 videos|242 docs|187 tests
|
FAQs on NCERT Solutions for Class 10 Maths Chapter 1 - Real Numbers (Exercise 1.4)
| 1. What are real numbers? |  |
| 2. What is the difference between rational and irrational numbers? |  |
| 3. How do you determine if a number is irrational? |  |
| 4. What is the significance of real numbers in mathematics? |  |
| 5. Can real numbers be negative? |  |






















