NCERT Solutions for Class 10 Maths Chapter 2 - Polynomials (Exercise 2.1)
Exercise 2.1
Q1: The graphs of y = p(x) are given in Fig. 2.10 below, for some polynomials p(x). Find the number of zeroes of p(x), in each case.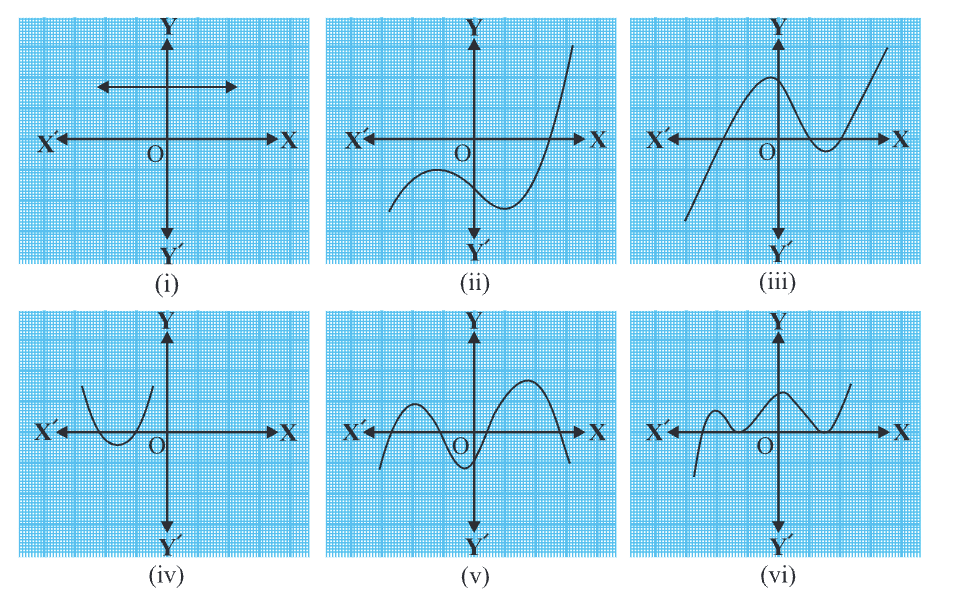
Sol:
Graphical method to find zeroes:
Total number of zeroes in any polynomial equation = total number of times the curve intersects x-axis.
(i) In the given graph, the number of zeroes of p(x) is 0 because the graph is parallel to x-axis does not cut it at any point.
(ii) In the given graph, the number of zeroes of p(x) is 1 because the graph intersects the x-axis at only one point.
(iii) In the given graph, the number of zeroes of p(x) is 3 because the graph intersects the x-axis at any three points.
(iv) In the given graph, the number of zeroes of p(x) is 2 because the graph intersects the x-axis at two points.
(v) In the given graph, the number of zeroes of p(x) is 4 because the graph intersects the x-axis at four points.
(vi) In the given graph, the number of zeroes of p(x) is 3 because the graph intersects the x-axis at three points.
(Exercise 2.2)
Q1: Find the zeroes of the following quadratic polynomials and verify the relationship between the zeroes and the coefficients.
(i) x2–2x –8
Sol: ⇒x2– 4x+2x–8 = x(x–4)+2(x–4) = (x-4)(x+2)
Therefore, zeroes of polynomial equation x2–2x–8 are (4, -2)
Sum of zeroes = 4–2 = 2 = -(-2)/1 = -(Coefficient of x)/(Coefficient of x2)
Product of zeroes = 4×(-2) = -8 =-(8)/1 = (Constant term)/(Coefficient of x2)
(ii) 4s2–4s+1
Sol: ⇒4s2–2s–2s+1 = 2s(2s–1)–1(2s-1) = (2s–1)(2s–1)
Therefore, zeroes of polynomial equation 4s2–4s+1 are (1/2, 1/2)
Sum of zeroes = (½)+(1/2) = 1 = -(-4)/4 = -(Coefficient of s)/(Coefficient of s2)
Product of zeros = (1/2)×(1/2) = 1/4 = (Constant term)/(Coefficient of s2 )
(iii) 6x2–3–7x
Sol: ⇒6x2–7x–3 = 6x2 – 9x + 2x – 3 = 3x(2x – 3) +1(2x – 3) = (3x+1)(2x-3)
Therefore, zeroes of polynomial equation 6x2–3–7x are (-1/3, 3/2)
Sum of zeroes = -(1/3)+(3/2) = (7/6) = -(Coefficient of x)/(Coefficient of x2)
Product of zeroes = -(1/3)×(3/2) = -(1/2) = (Constant term) /(Coefficient of x2 )
(iv) 4u2+8u
Sol: ⇒ 4u(u+2)
Therefore, zeroes of polynomial equation 4u2 + 8u are (0, -2).
Sum of zeroes = 0+(-2) = -2 = -(8/4) = = -(Coefficient of u)/(Coefficient of u2)
Product of zeroes = 0×-2 = 0 = 0/4 = (Constant term)/(Coefficient of u2 )
(v) t2–15
⇒ t2 = 15 or t = ± √15
Therefore, zeroes of polynomial equation t2 –15 are (√15, -√15)
Sum of zeroes =√15 + (-√15) = 0 = -(0/1)= -(Coefficient of t) / (Coefficient of t2)
Product of zeroes = √15 × (-√15) = -15 = -15/1 = (Constant term) / (Coefficient of t2 )
(vi) 3x2–x–4
⇒ 3x2–4x+3x–4 = x(3x-4)+1(3x-4) = (3x – 4)(x + 1)
Therefore, zeroes of polynomial equation3x2 – x – 4 are (4/3, -1)
Sum of zeroes = (4/3)+(-1) = (1/3)= -(-1/3) = -(Coefficient of x) / (Coefficient of x2)
Product of zeroes=(4/3)×(-1) = (-4/3) = (Constant term) /(Coefficient of x2 )
Q2: Find a quadratic polynomial each with the given numbers as the sum and product of its zeroes, respectively.
(i) 1/4 , -1
Sol: From the formulas of sum and product of zeroes, we know,
Sum of zeroes = α+β
Product of zeroes = α β
Sum of zeroes = α+β = 1/4
Product of zeroes = α β = -1
∴ If α and β are zeroes of any quadratic polynomial, then the quadratic polynomial equation can be written directly as:-
x2– (α+β) x + αβ = 0
x2–(1/4)x +(-1) = 0
4x2–x-4 = 0
Thus, 4x2– x – 4 is the quadratic polynomial.
(ii) √2, 1/3
Sol: Sum of zeroes = α + β =√2
Product of zeroes = α β = 1/3
∴ If α and β are zeroes of any quadratic polynomial, then the quadratic polynomial equation can be written directly as:-
x2– (α+β) x + αβ = 0
x2 –(√2)x + (1/3) = 0
3x2-3√2x+1 = 0
Thus, 3x2 - 3√2x + 1 is the quadratic polynomial.
(iii) 0, √5
Sol: Given,
Sum of zeroes = α+β = 0
Product of zeroes = α β = √5
∴ If α and β are zeroes of any quadratic polynomial, then the quadratic polynomial equation can be written directly as:-
x2– (α+β) x + αβ = 0
x2–(0)x +√5= 0
Thus, x2 + √5 is the quadratic polynomial.
(iv) 1, 1
Sol: Given,
Sum of zeroes = α+β = 1
Product of zeroes = α β = 1
∴ If α and β are zeroes of any quadratic polynomial, then the quadratic polynomial equation can be written directly as:-
x2– (α+β) x + αβ = 0
x2–x+1 = 0
Thus, x2 – x + 1 is the quadratic polynomial.
(v) -1/4, 1/4
Sol: Given,
Sum of zeroes = α+β = -1/4
Product of zeroes = α β = 1/4
∴ If α and β are zeroes of any quadratic polynomial, then the quadratic polynomial equation can be written directly as:-
x2– (α+β) x + αβ = 0
x2–(-1/4)x +(1/4) = 0
4x2+x+1 = 0
Thus, 4x2 + x + 1 is the quadratic polynomial.
(vi) 4, 1
Sol: Given,
Sum of zeroes = α+β =4
Product of zeroes = αβ = 1
∴ If α and β are zeroes of any quadratic polynomial, then the quadratic polynomial equation can be written directly as:-
x2– (α+β) x + αβ = 0
x2–4x+1 = 0
Thus, x2– 4x + 1 is the quadratic polynomial.
|
127 videos|584 docs|79 tests
|
FAQs on NCERT Solutions for Class 10 Maths Chapter 2 - Polynomials (Exercise 2.1)
| 1. What are polynomials and how are they classified? |  |
| 2. How do you add and subtract polynomials? |  |
| 3. What is the significance of the Remainder Theorem in polynomial division? |  |
| 4. How can you factor polynomials, and why is it important? |  |
| 5. What are the types of zeros of a polynomial, and how can they be determined? |  |






















