Class 9 Maths Chapter 6 Question Answers - Lines and Angles
Q.1. What is the measure of an angle whose measure is 32° less than its supplement?
Sol. Let the required angle be x
∴ x = (180°- x) - 32°
⇒ x = 74°
Q.2. If the supplement of an angle is 4 times its complement, find the angle.
Sol. Let the required angle be x
∴ (180°- x) = 4 (90° - x)
⇒ x = 60°
Q.3. An exterior angle of a Δ is 110° and its two opposite interior angles are equal. What is the measure of each angle?
Sol. Let each of the interior opposite angle be x
∴ x + x = 110°
⇒ x = 55°
Q.4. In a rt. ΔABC, ∠A = 90° and AB = AC. What are the values of ∠B and ∠C?
Sol. ∵ AB = AC
⇒ ∠B = ∠C
Also, ∠A = 90°
⇒ ∠B + ∠C = 90°
⇒ ∠B = ∠C = (90o/2) = 45°
Q.5. In the figure, what is the value of x?
Sol. ∵ ℓ || m and p is a transversal
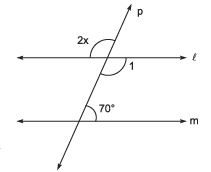
∴ ∠1 + 70° = 180° [co-interior angles]
⇒ ∠1 = 180° - 70° = 110°
Now, 2x = 110° [vertically opposite angles]
⇒ x =(110°/2) = 55°
Q.6. If two interior angles on the same side of a transversal intersecting two parallel lines are in the ratio 2 : 3 then, what is the smaller angle?
Sol. ℓ || m and p is the transversal
∴ ‘a’ and ‘b’ are interior angles on the same side of the transversal p.
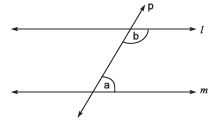
Let a = 2x and b = 3x
∴ a + b = 180°
⇒ 2x + 3x = 180°
⇒ 5x = 180°
⇒ x = (180/5)= 36°
∴ smaller angle = 2x = 2 x 36 = 72°
Q.7. In the figure, what is the measure of ∠ ABC?
Sol. ∠PAQ = ∠BAC [vertically opp. angles]
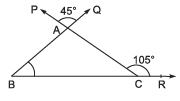
Now, ext. ∠ACR= ∠ABC + ∠BAC = 105°
⇒ ∠ABC = 105° - 45° = 60°
Q.8. In the following figure AB || CD. Find the measure of ∠BOC.
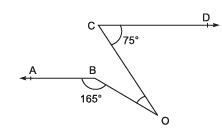
Sol. Extending AB to intersect OC, we get the following figure.
ABF is a straight line
∴ ∠OBF = 180° - 165° = 15°
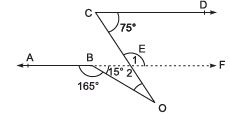
AB || CD ⇒ EF || CD
∴ ∠1 + 75° = 180°
⇒ ∠1 = 180° - 75° = 105°
⇒ ∠2 = 105°
Now, in Δ, ∠2 + 15° + ∠BOC = 180°
⇒ 105° + 15° + ∠BOC = 180°
⇒ ∠BOC = 180° - 105° - 15°
= 60°
|
40 videos|471 docs|57 tests
|
FAQs on Class 9 Maths Chapter 6 Question Answers - Lines and Angles
| 1. What are lines and angles? |  |
| 2. What is the difference between a line and a line segment? |  |
| 3. How do you classify angles based on their measurements? |  |
| 4. What are complementary angles? |  |
| 5. How do you identify parallel lines? |  |






















