NCERT Solutions for Class 9 Maths Chapter 7 - Triangles (Exercise 7.1-7.3)
Exercise 7.1
Q1. In quadrilateral ACBD, AC = AD and AB bisects ∠ A. Show that ∆ ABC ≅ ∆ ABD. What can you say about BC and BD?
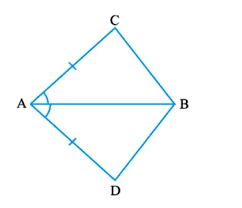
Ans: It is given that AC and AD are equal i.e. AC = AD and the line segment AB bisects ∠A.
We will have to now prove that the two triangles ABC and ABD are congruent i.e. ΔABC ≅ ΔABD
Proof:
Consider the triangles ΔABC and ΔABD,
(i) AC = AD (It is given in the question)
(ii) AB = AB (Common
(iii) ∠CAB = ∠DAB (Since AB is the bisector of angle A)
So, by SAS congruency criterion, ΔABC ≅ ΔABD.
For the 2nd part of the question, BC and BD are of equal lengths by CPCT.
Q2. ABCD is a quadrilateral in which AD = BC and ∠ DAB = ∠ CBA. Prove that
(i) ∆ ABD ≅ ∆ BAC
(ii) BD = AC
(iii) ∠ ABD = ∠ BAC
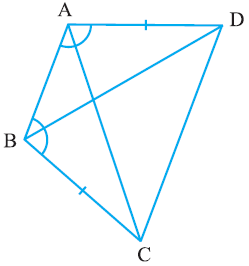
Ans: The given parameters from the questions are ∠DAB = ∠CBA and AD = BC.
(i) ΔABD and ΔBAC are similar by SAS congruency as
AB = BA (It is the common arm)
∠DAB = ∠CBA and AD = BC (These are given in the question)
So, triangles ABD and BAC are similar i.e. ΔABD ≅ ΔBAC. (Hence proved).
(ii) It is now known that ΔABD ≅ ΔBAC so,
BD = AC (by CPCT).
(iii) Since ΔABD ≅ ΔBAC so,
Angles ∠ABD = ∠BAC (by CPCT).
Q3. AD and BC are equal perpendiculars to a line segment AB. Show that CD bisects AB.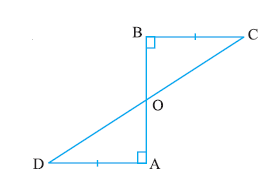
Ans:
Given: AD ⊥ AB at A, BC ⊥ AB at B, and AD = BC.
1. Consider △ADC and △BCD:
• ∠ADC = ∠BCD = 90° (each is angle between AD (or BC) and CD).
• AD = BC (given).
• CD is common.
Thus △ADC ≅ △BCD (RHS).
2. Hence ∠ACD = ∠CBD (CPCT).
These are angles with vertex on AB, so CD makes equal angles with AB at A and B.
Therefore, CD is the perpendicular bisector of AB, i.e., it bisects AB.
Q4. l and m are two parallel lines intersected by another pair of parallel lines p and q. Show that ∆ ABC ≅ ∆ CDA.
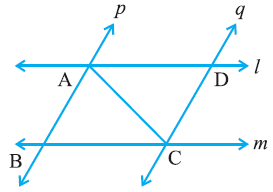
Ans: It is given that p || q and l || m
To prove:
Triangles ABC and CDA are similar i.e. ΔABC ≅ ΔCDA
Proof:
Consider the ΔABC and ΔCDA,
(i) ∠BCA = ∠DAC and ∠BAC = ∠DCA Since they are alternate interior angles
(ii) AC = CA as it is the common arm
So, by ASA congruency criterion, ΔABC ≅ ΔCDA.
Q5. Line l is the bisector of an angle ∠ A and B is any point on l. BP and BQ are perpendiculars from B to the arms of ∠ A. Show that:
(i) ∆ APB ≅ ∆ AQB
(ii) BP = BQ or B is equidistant from the arms of ∠ A.
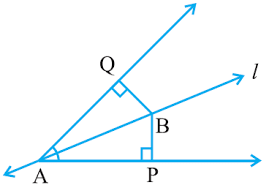
Ans:
Given: Line l is the bisector of an angle ∠A and B is any point on l.
To prove: (i) Δ APB ≅ Δ AQB
(ii) BP = BQ or B is equidistant from the arms of ∠A.
In ∆APB , ∆AQB,
∠APB = ∠AQB (Each right angle )
∠PAB = ∠QAB (l is the angle bisector of ∠A)
AB = AB (Common)
∴ ∆APB ≅ ∆AQB (By AAS congruence rule)
∴ BP = BQ (By CPCT)
Or, it can be said that B is equidistant from the arms of ∠A.
Q6. In the following figure, AC = AE, AB = AD and ∠ BAD = ∠ EAC. Show that BC = DE.
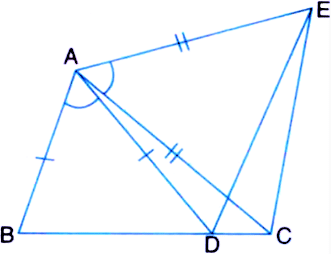
Ans: It is given in the question that AB = AD, AC = AE, and ∠BAD = ∠EAC
To prove:
The line segment BC and DE are similar i.e. BC = DE
Proof:
We know that ∠BAD = ∠EAC
Now, by adding ∠DAC on both sides we get,
∠BAD + ∠DAC = ∠EAC +∠DAC
This implies, ∠BAC = ∠EAD
Now, ΔABC and ΔADE are similar by SAS congruency since:
(i) AC = AE (As given in the question)
(ii) ∠BAC = ∠EAD
(iii) AB = AD (It is also given in the question)
∴ Triangles ABC and ADE are similar i.e. ΔABC ≅ ΔADE.
So, by CPCT, it can be said that BC = DE.
Q7. AB is a line segment and P is its mid-point. D and E are points on the same side of AB such that ∠ BAD = ∠ ABE and ∠ EPA = ∠ DPB. Show that
(i) ∆ DAP ≅ ∆ EBP
(ii) AD = BE
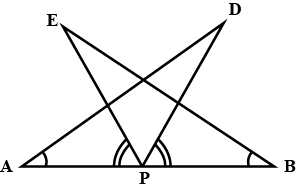
Ans:
Given: AB is a line segment and P is its mid-point. D and E are points on the same side of AB such that ∠BAD = ∠ABE and ∠ EPA = ∠ DPB
To prove: (i) Δ DAP ≅ Δ EBP
(ii) AD = BE
It is given that ∠EPA = ∠DPB
∠EPA + ∠DPE = ∠DPB + ∠DPE
∴ ∠DPA = ∠EPB
In ∆DAP and ∆EBP,
∠DAP = ∠EBP (Given)
AP = BP (P is mid-point of AB)
∠DPA = ∠EPB (From above)
∴ ∆DAP ≅ ∆EBP (ASA congruence rule)
∴ AD = BE (By CPCT)
Q8. In right triangle ABC, right angled at C, M is the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B. Show that:
(i) ∆ AMC ≅ ∆ BMD
(ii) ∠ DBC is a right angle.
(iii) ∆ DBC ≅ ∆ ACB
(iv) CM = ½ AB
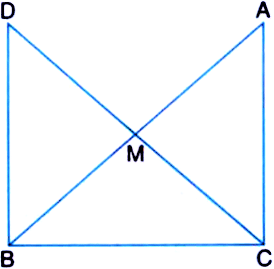
Ans: It is given that M is the mid-point of the line segment AB, ∠C = 90°, and DM = CM
(i) Consider the triangles ΔAMC and ΔBMD:
AM = BM (Since M is the mid-point)
CM = DM (Given in the question)
∠CMA = ∠DMB (They are vertically opposite angles)
So, by SAS congruency criterion, ΔAMC ≅ ΔBMD.
(ii) ∠ACM = ∠BDM (by CPCT)
∴ AC || BD as alternate interior angles are equal.
Now, ∠ACB +∠DBC = 180° (Since they are co-interior angles)
⇒ 90° +∠B = 180°
∴ ∠DBC = 90°
(iii) In ΔDBC and ΔACB,
BC = CB (Common side)
∠ACB = ∠DBC (They are right angles)
DB = AC (by CPCT)
So, ΔDBC ≅ ΔACB by SAS congruency.
(iv) DC = AB (Since ΔDBC ≅ ΔACB)
⇒ DM = CM = AM = BM (Since M the is mid-point)
So, DM + CM = BM+AM
Hence, CM + CM = AB
⇒ CM = (½) AB
Exercise 7.2
Q1. In an isosceles triangle ABC, with AB = AC, the bisectors of ∠ B and ∠ C intersect each other at O. Join A to O. Show that:
(i) OB = OC
(ii) AO bisects ∠ A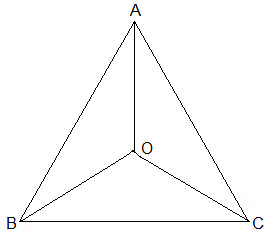
Ans:
Given:
AB = AC and
the bisectors of ∠B and ∠C intersect each other at O
(i) Since ABC is an isosceles with AB = AC,
∠B = ∠C
½ ∠B = ½ ∠C
⇒ ∠OBC = ∠OCB (Angle bisectors)
∴ OB = OC (Side opposite to the equal angles are equal.)
(ii) In ΔAOB and ΔAOC,
AB = AC (Given in the question)
AO = AO (Common arm)
OB = OC (As Proved Already)
So, ΔAOB ≅ ΔAOC by SSS congruence condition.
BAO = CAO (by CPCT)
Thus, AO bisects ∠A.
Q2. In ΔABC, AD is the perpendicular bisector of BC (see Fig.). Show that ΔABC is an isosceles triangle in which AB = AC.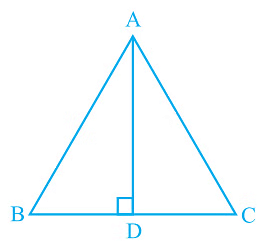
Ans: It is given that AD is the perpendicular bisector of BC
To prove:
AB = AC
Proof:
In ΔADB and ΔADC,
AD = AD (It is the Common arm)
∠ADB = ∠ADC
BD = CD (Since AD is the perpendicular bisector)
So, ΔADB ≅ ΔADC by SAS congruency criterion.
Thus,
AB = AC (by CPCT)
Q3. ABC is an isosceles triangle in which altitudes BE and CF are drawn to equal sides AC and AB respectively (see Fig.). Show that these altitudes are equal.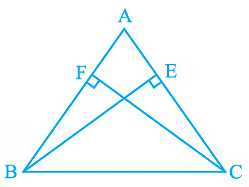
Ans:
Given:
(i) BE and CF are altitudes.
(ii) AC = AB
To prove:
BE = CF
Proof:
Triangles ΔAEB and ΔAFC are similar by AAS congruency since
∠A = ∠A (It is the common arm)
∠AEB = ∠AFC (They are right angles)
AB = AC (Given in the question)
∴ ΔAEB ≅ ΔAFC and so, BE = CF (by CPCT).
Q4. ABC is a triangle in which altitudes BE and CF to sides AC and AB are equal (see Fig). Show that
(i) ∆ ABE ≅ ∆ ACF
(ii) AB = AC, i.e., ABC is an isosceles triangle.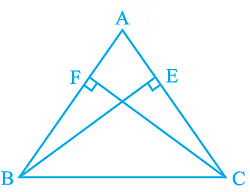
Ans: It is given that BE = CF
(i) In ΔABE and ΔACF,
∠A = ∠A (It is the common angle)
∠AEB = ∠AFC (They are right angles)
BE = CF (Given in the question)
∴ ΔABE ≅ ΔACF by AAS congruency condition.
(ii) AB = AC by CPCT and so, ABC is an isosceles triangle.
Q5. ABC and DBC are two isosceles triangles on the same base BC (see Fig). Show that ∠ ABD = ∠ ACD.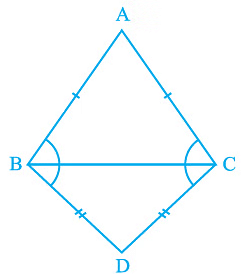
Ans: In the question, it is given that ABC and DBC are two isosceles triangles.
We will have to show that ∠ABD = ∠ACD
Proof:
Triangles ΔABD and ΔACD are similar by SSS congruency since
AD = AD (It is the common arm)
AB = AC (Since ABC is an isosceles triangle)
BD = CD (Since BCD is an isosceles triangle)
So, ΔABD ≅ ΔACD.
∴ ∠ABD = ∠ACD by CPCT.
Q6. ∆ABC is an isosceles triangle in which AB = AC. Side BA is produced to D such that AD = AB (see Fig). Show that ∠ BCD is a right angle.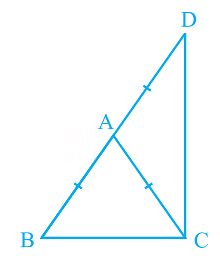
Ans: It is given that AB = AC and AD = AB
We will have to now prove ∠BCD is a right angle.
Proof:
Consider ΔABC,
AB = AC (It is given in the question)
Also, ∠ACB = ∠ABC (They are angles opposite to the equal sides and so, they are equal)
Now, consider ΔACD,
AD = AB
Also, ∠ADC = ∠ACD (They are angles opposite to the equal sides and so, they are equal)
Now,
In ΔABC,
∠CAB + ∠ACB + ∠ABC = 180°
So, ∠CAB + 2∠ACB = 180°
⇒ ∠CAB = 180° – 2∠ACB — (i)
Similarly, in ΔADC,
∠CAD = 180° – 2∠ACD — (ii)
also,
∠CAB + ∠CAD = 180° (BD is a straight line.)
Adding (i) and (ii) we get,
∠CAB + ∠CAD = 180° – 2∠ACB+180° – 2∠ACD
⇒ 180° = 360° – 2∠ACB-2∠ACD
⇒ 2(∠ACB+∠ACD) = 180°
⇒ ∠BCD = 90°
Q7. ABC is a right angled triangle in which ∠ A = 90° and AB = AC. Find ∠ B and ∠ C.
Ans: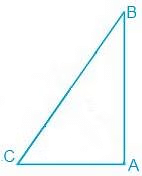
In the question, it is given that
∠A = 90° and AB = AC
AB = AC
⇒ ∠B = ∠C (They are angles opposite to the equal sides and so, they are equal)
Now,
∠A+∠B+∠C = 180° (Since the sum of the interior angles of the triangle)
∴ 90° + 2∠B = 180°
⇒ 2∠B = 90°
⇒ ∠B = 45°
So, ∠B = ∠C = 45°
Q8. Show that the angles of an equilateral triangle are 60° each.
Ans: Let ABC be an equilateral triangle as shown below: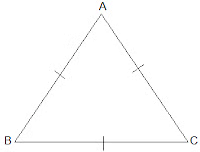 Here, BC = AC = AB (Since the length of all sides is same)⇒ ∠A = ∠B =∠C (Sides opposite to the equal angles are equal.)Also, we know that
Here, BC = AC = AB (Since the length of all sides is same)⇒ ∠A = ∠B =∠C (Sides opposite to the equal angles are equal.)Also, we know that
∠A+∠B+∠C = 180°
⇒ 3∠A = 180°
⇒ ∠A = 60°
∴ ∠A = ∠B = ∠C = 60°
So, the angles of an equilateral triangle are always 60° each.
Exercise 7.3
Q1. ∆ ABC and ∆ DBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (see Fig). If AD is extended to intersect BC at P, show that
(i) ΔABD ≅ ΔACD
(ii) ΔABP ≅ ΔACP
(iii) AP bisects ∠A as well as ∠D.
(iv) AP is the perpendicular bisector of BC.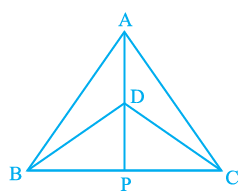
Ans:
(i) In ∆ABD and ∆ACD,
AB = AC
[Equal sides of isosceles triangle]
DB = DC
[Equal sides of isosceles triangle]
AD = AD (Common)
∴ ∆ABD ≅ ∆ACD [By SSS]
⇒ ∠BAD = ∠CAD (CPCT)
⇒ ∠BAP = ∠CAP …. (1)
And ∠ADB = ∠ADC (CPCT) … (2)
(ii) In ∆ABP and ∆ACP
AB = AC
[Equal sides of isosceles triangle]
∠BAP = ∠CAP [From 1]
AP = AP (Common)
∴ ΔABP ≅ ΔACP
[By SAS]
∴ BP = CP (CPCT) … (3)
Similarly, ∠APB = ∠APC (CPCT) … (4)
(ii) AP is bisector of ∠A
[From 1]
Now, since AP is a line segment
∴ ∠ADB + ∠BDP = 180° … (5)
Similarly, ∠ADC + ∠CDP = 180° … (6)
Comparing equations 2, 5 and 6 we can say that
∠BDP = ∠CDP
∴ AP bisects ∠D
Hence AP bisects both ∠A and ∠D
(iv) We know,
∠APB + ∠APC = 180°
⇒ ∠APB + ∠APB = 180°
[From 4]
⇒ ∠APB = 90° … (7)
From equations 3 and 7 we can say that,
AP is perpendicular bisector of BC.
Q2. AD is an altitude of an isosceles triangle ABC in which AB = AC. Show that
(i) AD bisects BC
(ii) AD bisects ∠ A.
Ans: It is given that AD is an altitude and AB = AC. The diagram is as follows: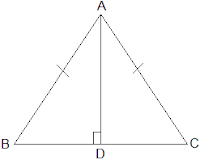
(i) In ΔABD and ΔACD,
∠ADB = ∠ADC = 90°
AB = AC (It is given in the question)
AD = AD (Common arm)
∴ ΔABD ≅ ΔACD by RHS congruence condition.
Now, by the rule of CPCT,
BD = CD.
So, AD bisects BC
(ii) Again, by the rule of CPCT, ∠BAD = ∠CAD
Hence, AD bisects ∠A.
Q3. Two sides AB and BC and median AM of one triangle ABC are respectively equal to sides PQ and QR and median PN of ΔPQR (see Fig). Show that:
(i) ΔABM ≅ ΔPQN
(ii) ΔABC ≅ ΔPQR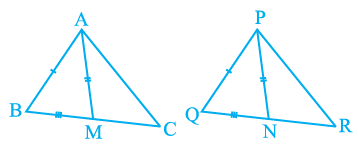
Ans: Given parameters are:
AB = PQ,
BC = QR and
AM = PN
(i) ½ BC = BM and ½ QR = QN (Since AM and PN are medians)
Also, BC = QR
So, ½ BC = ½ QR
⇒ BM = QN
In ΔABM and ΔPQN,
AM = PN and AB = PQ (As given in the question)
BM = QN (Already proved)
∴ ΔABM ≅ ΔPQN by SSS congruency.
(ii) In ΔABC and ΔPQR,
AB = PQ and BC = QR (As given in the question)
∠ABC = ∠PQR (by CPCT)
So, ΔABC ≅ ΔPQR by SAS congruency.
Q4. BE and CF are two equal altitudes of a triangle ABC. Using RHS congruence rule, prove that the triangle ABC is isosceles.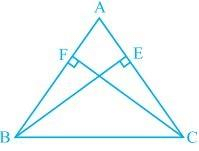
Ans: It is known that BE and CF are two equal altitudes.
Now, in ΔBEC and ΔCFB,
∠BEC = ∠CFB = 90° (Same Altitudes)
BC = CB (Common side)
BE = CF (Given)
So, ΔBEC ≅ ΔCFB by RHS congruence criterion.
Also, ∠C = ∠B (by CPCT)
Therefore, AB = AC as sides opposite to the equal angles is always equal.
Q5. ABC is an isosceles triangle with AB = AC. Draw AP ⊥ BC to show that ∠ B = ∠ C.
Ans: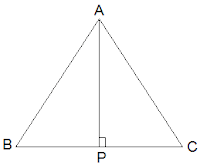
In the question, it is given that AB = AC
Now, ΔABP and ΔACP are similar by RHS congruency as
∠APB = ∠APC = 90° (AP is altitude)
AB = AC (Given in the question)
AP = AP (Common side)
So, ΔABP ≅ ΔACP.
∴ ∠B = ∠C (by CPCT)
|
40 videos|471 docs|57 tests
|
FAQs on NCERT Solutions for Class 9 Maths Chapter 7 - Triangles (Exercise 7.1-7.3)
| 1. What are the different types of triangles? |  |
| 2. How do you find the area of a triangle? |  |
| 3. What is the Pythagorean theorem? |  |
| 4. How do you determine if three given side lengths form a triangle? |  |
| 5. What is the sum of angles in a triangle? |  |

















