NCERT Solutions for Class 10 Maths Chapter 3 - Pair of Linear Equations in Two Variables (Exercise 3.1)
Exercise 3.1
Q1. Form the pair of linear equations in the following problems, and find their solutions graphically.
(i) 10 students of Class X took part in a Mathematics quiz. If the number of girls is 4 more than the number of boys, find the number of boys and girls who took part in the quiz.
(ii) 5 pencils and 7 pens together cost 50, whereas 7 pencils and 5 pens together cost 46. Find the cost of one pencil and that of one pen.
Ans: (i)
Let number of boys = x
Number of girls = y
Given that total number of student is 10.
So, x + y = 10
Subtract y both side we get,
x = 10 – y
Putting y = 0 , 5, 10 we get,
x = 10 – 0 = 10
x = 10 – 5 = 5
x = 10 – 10 = 0
| x | 10 | 5 |
| y | 0 | 5 |
Given that If the number of girls is 4 more than the number of boys.
So, y = x + 4
Putting x = -4, 0, 4, and we get,
y = - 4 + 4 = 0
y = 0 + 4 = 4
y = 4 + 4 = 8
| x | -4 | 0 | 4 |
| y | 0 | 4 | 8 |
Graphical representation: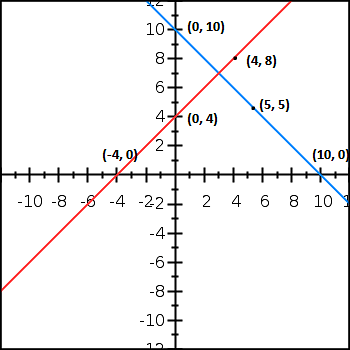 Therefore, number of boys = 3 and number of girls = 7
Therefore, number of boys = 3 and number of girls = 7
(ii) Let 1 pencil costs Rs.x and 1 pen costs Rs.y.
According to the question, the algebraic expression cab be represented as;
5x + 7y = 50
7x + 5y = 46
For, 5x + 7y = 50 or x = (50 - 7y) / 5, the solutions are;
| x | 3 | 0 |
| y | 5 | 7.14 |
For 7x + 5y = 46 or x = (46 - 5y) / 7, the solutions are;
| x | 6.57 | 3 |
| y | 0 | 5 |
Hence, the graphical representation is as follows: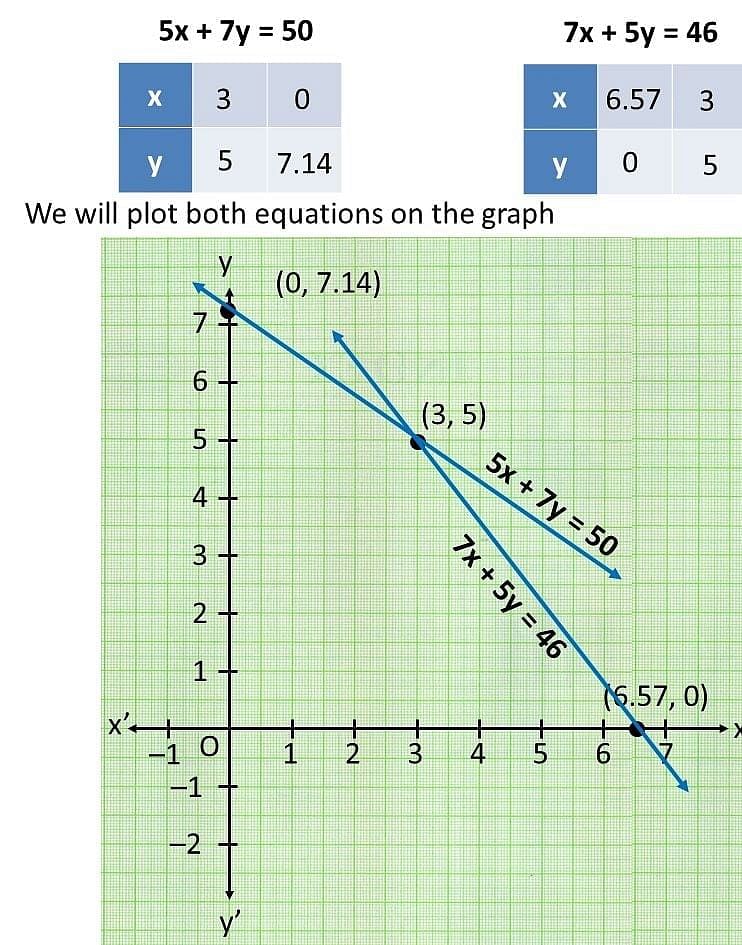
From the graph, it can be seen that the given lines cross each other at point (3, 5).So, the cost of a pencil is Rs. 3 and cost of a pen is Rs. 5.
Q2. On comparing the ratios a1 / a2 , b1 / b2 , c1 / c2 find out whether the lines representing the following pairs of linear equations intersect at a point, are parallel or coincident:
(i) 5x – 4y + 8 = 0
7x + 6y – 9 = 0
(ii) 9x + 3y + 12 = 0
18x + 6y + 24 = 0
(iii) 6x – 3y + 10 = 0
2x – y + 9 = 0
Ans: (i) Given expressions;
5x − 4y + 8 = 0
7x + 6y − 9 = 0
Comparing these equations with a1x + b1y + c1 = 0
And a2x + b2y + c2 = 0
We get,
a1 = 5, b1 = -4, c1 = 8
a2 = 7, b2 = 6, c2 = -9
(a1 / a2) = 5 / 7
(b1 / b2) = -4 / 6 = -2 / 3
(c1 / c2) = 8 / -9
Since, (a1 / a2) ≠ (b1 / b2)
So, the pairs of equations given in the question have a unique solution and the lines cross each other at exactly one point.
(ii) Given expressions;
9x + 3y + 12 = 0
18x + 6y + 24 = 0
Comparing these equations with a1x + b1y + c1 = 0
And a2x + b2y + c2 = 0
We get,
a1 = 9, b1 = 3, c1 = 12
a2 = 18, b2 = 6, c2= 24
(a1/ a2) = 9 / 18 = 1 / 2
(b1 / b2) = 3 / 6 = 1 / 2
(c1 / c2) = 12 / 24 = 1 / 2
Since (a1/ a2) = (b1 / b2) = (c1 / c2)
So, the pairs of equations given in the question have infinite possible solutions and the lines are coincident.
(iii) Given Expressions;
6x – 3y + 10 = 0
2x – y + 9 = 0
Comparing these equations with
a1x + b1y + c1 = 0
And a2x + b2y + c2= 0
We get,
a1 = 6, b1 = -3, c1 = 10
a2 = 2, b2= -1, c2= 9
(a1 / a2) = 6 / 2 = 3 / 1
(b1 / b2) = -3 / -1 = 3 / 1
(c1 / c2) = 10 / 9
Since (a1 / a2) = (b1 / b2) ≠ (c1 / c2)
So, the pairs of equations given in the question are parallel to each other and the lines never intersect each other at any point and there is no possible solution for the given pair of equations.
Q3. On comparing the ratio, (a1 / a2), (b1 / b2), (c1 / c2) find out whether the following pair of linear equations are consistent, or inconsistent.
(i) 3x + 2y = 5 ; 2x – 3y = 7
(ii) 2x – 3y = 8 ; 4x – 6y = 9
(iii) (3 / 2)x + (5 / 3)y = 7; 9x – 10y = 14
(iv) 5x – 3y = 11 ; – 10x + 6y = –22
(v) (4 / 3)x + 2y = 8 ; 2x + 3y = 12
Ans: (i) Given: 3x + 2y = 5 or 3x + 2y -5 = 0
and 2x – 3y = 7 or 2x – 3y -7 = 0
Comparing these equations with a1x + b1y + c1 = 0
And a2x + b2y + c2 = 0
We get,
a1 = 3, b1 = 2, c1 = -5
a2 = 2, b2= -3, c2= -7
(a1 / a2) = 3 / 2
(b1 / b2) = 2 / -3
(c1 / c2) = -5 / -7 = 5 / 7
Since, (a1 / a2) ≠ (b1 / b2)
So, the given equations intersect each other at one point and they have only one possible solution. The equations are consistent.
(ii) Given: 2x – 3y = 8 and 4x – 6y = 9
Therefore,
a1 = 2, b1 = -3, c1 = -8
a2= 4, b2= -6, c2 = -9
(a1 / a2) = 2 / 4 = 1 / 2
(b1 / b2) = -3 / -6 = 1 / 2
(c1 / c2) = -8 / -9 = 8 / 9
Since , (a1/ a2) = (b1/ b2) ≠ (c1 / c2)
So, the equations are parallel to each other and they have no possible solution. Hence, the equations are inconsistent.
(iii) Given: (3 / 2)x + (5 / 3)y = 7 and 9x – 10y = 14
Therefore,
a1= 3 / 2, b1= 5 / 3, c1 = -7
a2= 9, b2= -10, c2= -14
(a1/ a2) = 3 / (2 × 9) = 1 / 6
(b1/ b2) = 5 / (3× - 10)= -1 / 6
(c1 / c2) = -7 / -14 = 1 / 2
Since, (a1/ a2) ≠ (b1/ b2)
So, the equations are intersecting each other at one point and they have only one possible solution. Hence, the equations are consistent.
(iv) Given: 5x – 3y = 11 and – 10x + 6y = –22
Therefore,
a1= 5, b1 = -3, c1 = -11
a2= -10, b2 = 6, c2= 22
(a1/ a2) = 5 / (-10) = -5 / 10 = -1 / 2
(b1/ b2) = -3 / 6 = -1 / 2
(c1 / c2) = -11 / 22 = -1 / 2
Since (a1/ a2) = (b1/ b2) = (c1 / c2)
These linear equations are coincident lines and have infinite number of possible solutions. Hence, the equations are consistent.
(v) Given: (4 / 3)x + 2y = 8 and 2x + 3y = 12
a1= 4 / 3 , b1= 2 , c1 = -8
a2= 2, b2 = 3 , c2= -12
(a1/ a2) = 4 / (3 × 2)= 4 / 6 = 2 / 3
(b1/ b2) = 2 / 3
(c1 / c2) = -8 / -12 = 2 / 3
Since (a1/ a2) = (b1/ b2) = (c1 / c2)
These linear equations are coincident lines and have infinite number of possible solutions. Hence, the equations are consistent.
Q4. Which of the following pairs of linear equations are consistent/inconsistent? If consistent, obtain the solution graphically:
(i) x + y = 5, 2x + 2y = 10
(ii) x – y = 8, 3x – 3y = 16
(iii) 2x + y – 6 = 0, 4x – 2y – 4 = 0
(iv) 2x – 2y – 2 = 0, 4x – 4y – 5 = 0
Ans: (i) Given, x + y = 5 and 2x + 2y = 10
(a1/ a2) = 1 / 2
(b1/ b2) = 1 / 2
(c1 / c2) = 1 / 2
Since (a1/ a2) = (b1/ b2) = (c1 / c2)
∴The equations are coincident and they have infinite number of possible solutions.
So, the equations are consistent.
For, x + y = 5 or x = 5 – y
| x | 0 | 5 |
| y | 5 | 0 |
For 2x + 2y = 10 or x = (10 - 2y) / 2
| x | 0 | 5 |
| y | 5 | 0 |
So, the equations are represented in graphs as follows:
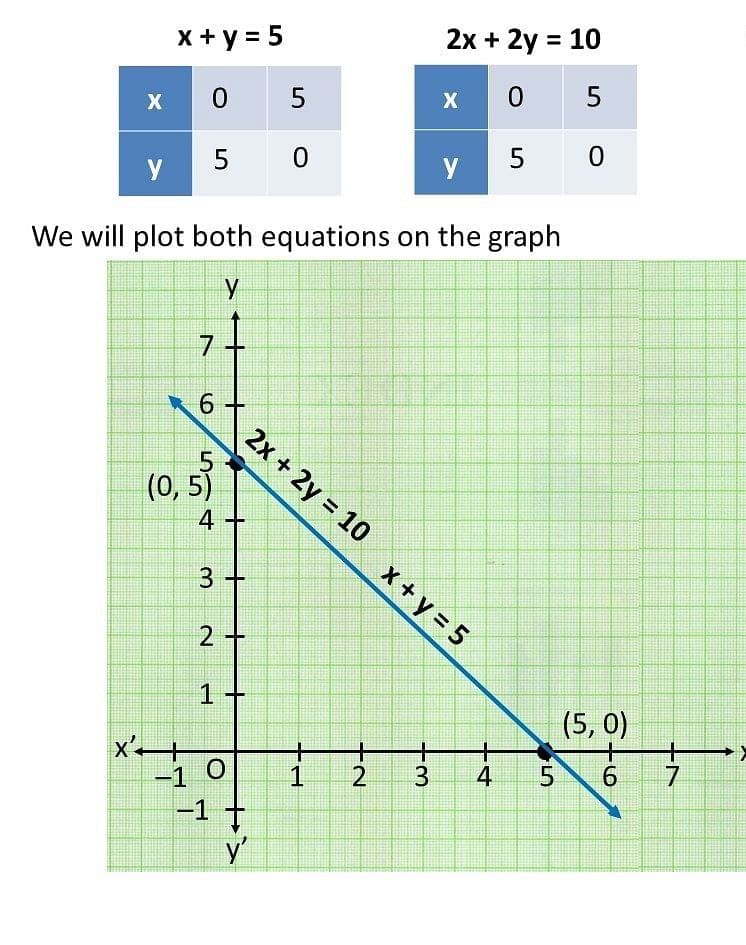 From the figure, we can see, that the lines are overlapping each other. Therefore, the equations have infinite possible solutions.
From the figure, we can see, that the lines are overlapping each other. Therefore, the equations have infinite possible solutions.
(ii) Given, x – y = 8 and 3x – 3y = 16
(a1/ a2) = 1 / 3
(b1/ b2) = -1 / -3 = 1 / 3
(c1 / c2) = 8 / 16 = 1 / 2
Since, (a1/ a2) = (b1/ b2) ≠ (c1 / c2)
The equations are parallel to each other and have no solutions. Hence, the pair of linear equations is inconsistent.
(iii) Given, 2x + y – 6 = 0 and 4x – 2y – 4 = 0
(a1/ a2) = 2 / 4 = 1 / 2
(b1/ b2) = 1 / -2
(c1 / c2) = -6 / -4 = 3 / 2
Since, (a1/ a2) ≠ (b1/ b2)
The given linear equations are intersecting each other at one point and have only one solution. Hence, the pair of linear equations is consistent.
Now, for 2x + y – 6 = 0 or y = 6 – 2x
| x | 0 | 3 |
| y | 6 | 0 |
And for 4x – 2y – 4 = 0 or y = (4x - 4) / 2
| x | 0 | 1 |
| y | -2 | 0 |
So, the equations are represented in graphs as follows:
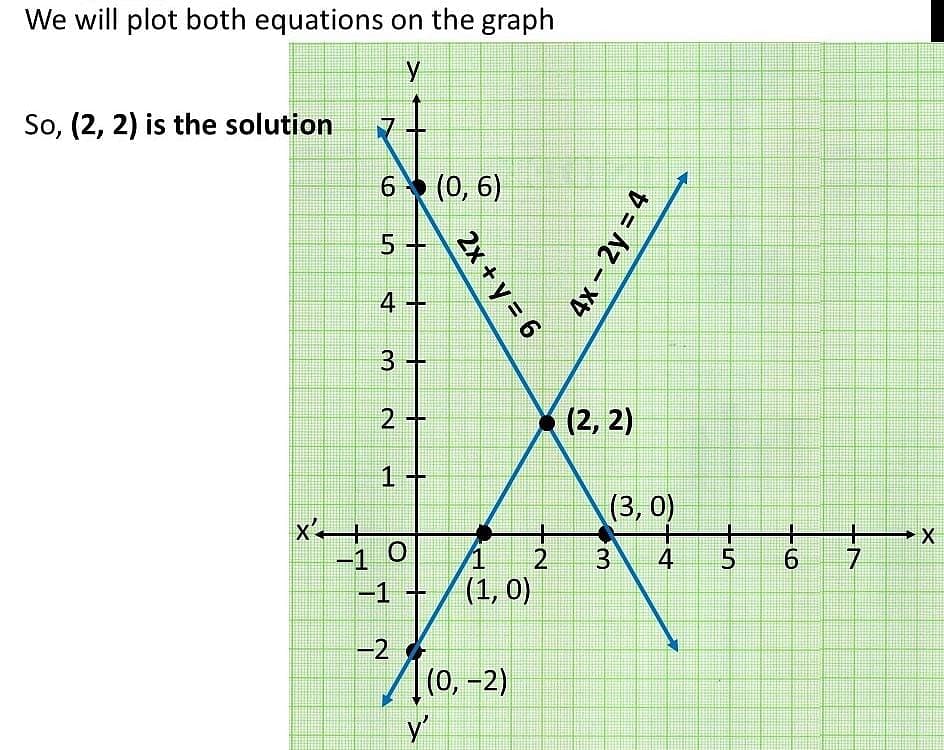 From the graph, it can be seen that these lines are intersecting each other at only one point (2,2).
From the graph, it can be seen that these lines are intersecting each other at only one point (2,2).
(iv) Given, 2x – 2y – 2 = 0 and 4x – 4y – 5 = 0
(a1/ a2) = 2 / 4 = 1 / 2
(b1/ b2) = -2 / -4 = 1 / 2
(c1 / c2) = 2 / 5
Since, a1/ a2= b1/ b2≠ c1 / c2
Thus, these linear equations have parallel and have no possible solutions. Hence, the pair of linear equations are inconsistent.
Q5. Half the perimeter of a rectangular garden, whose length is 4 m more than its width, is 36 m. Find the dimensions of the garden.
Ans: Let us consider.
The width of the garden is x and length is y.
Now, according to the question, we can express the given condition as;
x – y = 4
and
y + x = 36
Now, taking x – y = 4 or y = x + 4
| x | 4 | 0 |
| y | 0 | -4 |
For y + x = 36, y = 36 – x
| x | 12 | 20 |
| y | 24 | 16 |
The graphical representation of both the equation is as follows: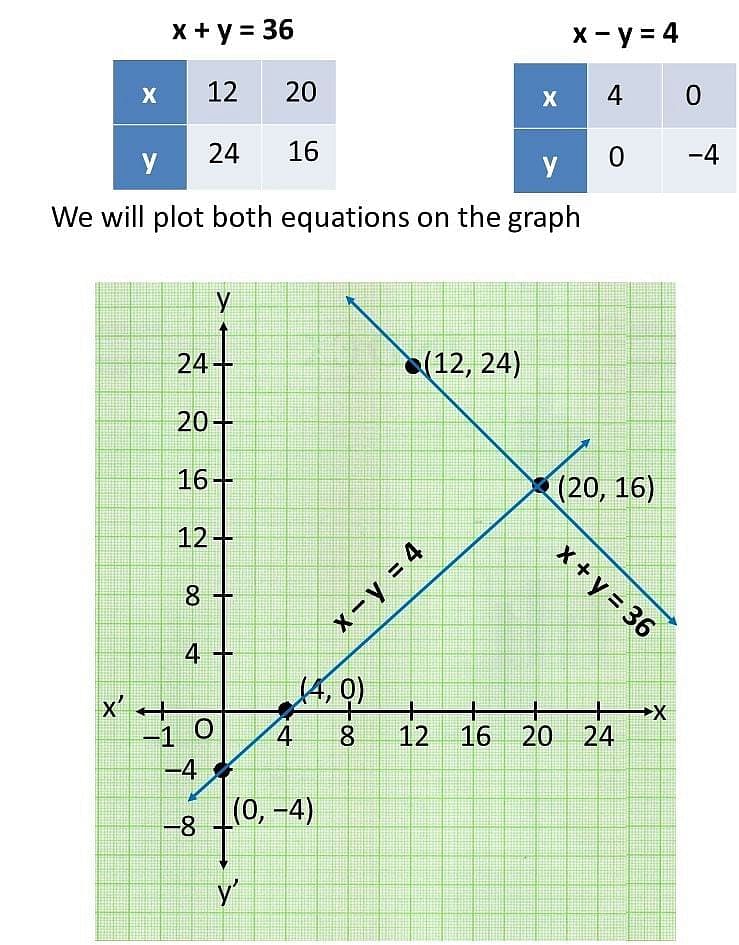 From the graph you can see, the lines intersects each other at a point(16, 20). Hence, the width of the garden is 16 and length is 20.
From the graph you can see, the lines intersects each other at a point(16, 20). Hence, the width of the garden is 16 and length is 20.
Q6. Given the linear equation 2x + 3y – 8 = 0, write another linear equation in two variables such that the geometrical representation of the pair so formed is:
(i) Intersecting lines
(ii) Parallel lines
(iii) Coincident lines
Ans: (i) Given the linear equation 2x + 3y – 8 = 0.
To find another linear equation in two variables such that the geometrical representation of the pair so formed is intersecting lines, it should satisfy below condition;
(a1/ a2) ≠ (b1/ b2)
Thus, another equation could be 2x – 7y + 9 = 0, such that;
(a1/ a2) = 2 / 2 = 1 and (b1/ b2) = 3 / -7
Clearly, you can see another equation satisfies the condition.
(ii) Given the linear equation 2x + 3y – 8 = 0.
To find another linear equation in two variables such that the geometrical representation of the pair so formed is parallel lines, it should satisfy below condition;
(a1/ a2) = (b1/ b2) ≠ (c1 / c2)
Thus, another equation could be 6x + 9y + 9 = 0, such that;
(a1/ a2) = 2 / 6 = 1 / 3
(b1/ b2) = 3 / 9= 1 / 3
(c1 / c2) = -8 / 9
Clearly, you can see another equation satisfies the condition.
(iii) Given the linear equation 2x + 3y – 8 = 0. To find another linear equation in two variables such that the geometrical representation of the pair so formed is coincident lines, it should satisfy below condition;
(a1/ a2) = (b1/ b2) = (c1 / c2)
Thus, another equation could be 4x + 6y – 16 = 0, such that;
(a1/ a2) = 2 / 4 = 1 / 2 ,(b1/ b2) = 3 / 6 = 1 / 2, (c1 / c2) = -8 / -16 = 1 / 2
Clearly, you can see another equation satisfies the condition.
Q7. Draw the graphs of the equations x – y + 1 = 0 and 3x + 2y – 12 = 0. Determine the coordinates of the vertices of the triangle formed by these lines and the x-axis, and shade the triangular region.
Ans: Given, the equations for graphs are x – y + 1 = 0 and 3x + 2y – 12 = 0.
For, x – y + 1 = 0 or x = 1 + y
| x | 0 | -1 |
| y | 1 | 0 |
For, 3x + 2y – 12 = 0 or x = (12 - 2y) / 3
| x | 0 | 4 |
| y | 6 | 0 |
Hence, the graphical representation of these equations is as follows:
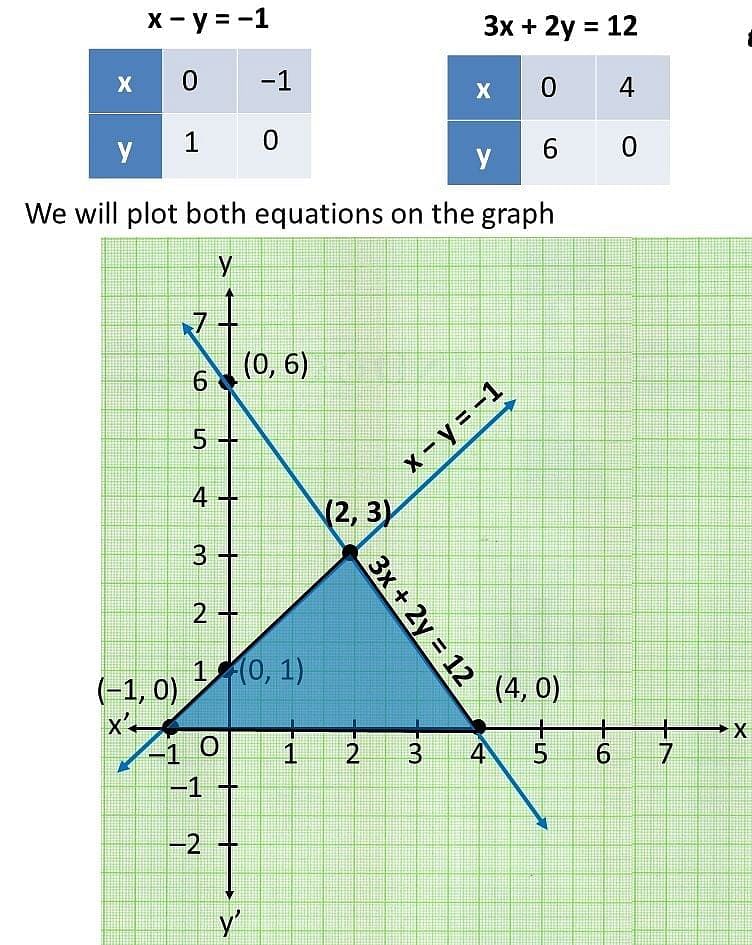
From the figure, it can be seen that these lines are intersecting each other at point (2, 3) and x-axis at (−1, 0) and (4, 0). Therefore, the vertices of the triangle are (2, 3), (−1, 0), and (4, 0).
Exercise 3.2
Q1: Solve the following pair of linear equations by the substitution method
(i) x + y = 14
x – y = 4
Sol: Given,
x + y = 14 and x – y = 4 are the two equations.
From 1st equation, we get,
x = 14 – y
Now, substitute the value of x in second equation to get,
(14 – y) – y = 4
14 – 2y = 4
2y = 10
Or y = 5
By the value of y, we can now find the exact value of x;
∵ x = 14 – y
∴ x = 14 – 5
Or x = 9
Hence, x = 9 and y = 5.
(ii) s – t = 3
(s/3) + (t/2) = 6
Sol: Given,
s – t = 3 and (s/3) + (t/2) = 6 are the two equations.
From 1st equation, we get,
s = 3 + t ________________(1)
Now, substitute the value of s in second equation to get,
(3+t)/3 + (t/2) = 6
⇒ (2(3+t) + 3t )/6 = 6
⇒ (6+2t+3t)/6 = 6
⇒ (6+5t) = 36
⇒5t = 30
⇒t = 6
Now, substitute the value of t in equation (1)
s = 3 + 6 = 9
Therefore, s = 9 and t = 6.
(iii) 3x – y = 3
9x – 3y = 9
Sol: 3x – y = 3 and 9x – 3y = 9 are the two equations.
From 1st equation, we get,
x = (3+y)/3
Now, substitute the value of x in the given second equation to get,
9(3+y)/3 – 3y = 9
⇒9 +3y -3y = 9
⇒ 9 = 9
Therefore, y has infinite values and since, x = (3+y) /3, so x also has infinite values.
(iv) 0.2x + 0.3y = 1.3
0.4x + 0.5y = 2.3
Sol: Given,
0.2x + 0.3y = 1.3 and 0.4x + 0.5y = 2.3are the two equations.
From 1st equation, we get,
x = (1.3- 0.3y)/0.2 _________________(1)
Now, substitute the value of x in the given second equation to get,
0.4(1.3-0.3y)/0.2 + 0.5y = 2.3
⇒ 2(1.3 – 0.3y) + 0.5y = 2.3
⇒ 2.6 – 0.6y + 0.5y = 2.3
⇒ 2.6 – 0.1 y = 2.3
⇒ 0.1 y = 0.3
⇒ y = 3
Now, substitute the value of y in equation (1), we get,
x = (1.3-0.3(3))/0.2 = (1.3-0.9)/0.2 = 0.4/0.2 = 2
Therefore, x = 2 and y = 3.
(v) √2 x + √3 y = 0
√3 x - √8 y = 0
Sol: Given,
√2 x + √3 y = 0 and √3 x – √8 y = 0
are the two equations.
From 1st equation, we get,
x = – (√3/√2)y __________________(1)
Putting the value of x in the given second equation to get,
√3(-√3/√2)y – √8y = 0 ⇒ (-3/√2)y- √8 y = 0
⇒ y = 0
Now, substitute the value of y in equation (1), we get,
x = 0
Therefore, x = 0 and y = 0.
(vi) (3x / 2) – (5y / 3) = -2
(x / 3) + (y / 2) = (13 / 6)
Sol: Given,
(3x/2)-(5y/3) = -2 and (x/3) + (y/2) = 13/6 are the two equations.
From 1st equation, we get,
(3/2)x = -2 + (5y/3)
⇒ x = 2(-6+5y)/9 = (-12+10y)/9 ………………………(1)
Putting the value of x in the given second equation to get,
((-12+10y)/9)/3 + y/2 = 13/6
⇒y/2 = 13/6 –( (-12+10y)/27 ) + y/2 = 13/6
Now, substitute the value of y in equation (1), we get,
(3x/2) – 5(3)/3 = -2
⇒ (3x/2) – 5 = -2
⇒ x = 2
Therefore, x = 2 and y = 3.
Q2: Solve 2x + 3y = 11 and 2x – 4y = – 24 and hence find the value of ‘m’ for which y = mx + 3.
Sol: 2x + 3y = 11…………………………..(I)
2x – 4y = -24………………………… (II)
From equation (II), we get
x = (11-3y)/2 ………………….(III)
Substituting the value of x in equation (II), we get
2(11-3y)/2 – 4y = 24
11 – 3y – 4y = -24
-7y = -35
y = 5……………………………………..(IV)
Putting the value of y in equation (III), we get
x = (11-3×5)/2 = -4/2 = -2
Hence, x = -2, y = 5
Also,
y = mx + 3
5 = -2m +3
-2m = 2
m = -1
Therefore the value of m is -1.
Q3: Form the pair of linear equations for the following problems and find their solution by substitution method.
(i) The difference between two numbers is 26 and one number is three times the other. Find them.
Sol: Let the two numbers be x and y respectively, such that y > x.
According to the question,
y = 3x ……………… (1)
y – x = 26 …………..(2)
Substituting the value of (1) into (2), we get
3x – x = 26
x = 13 ……………. (3)
Substituting (3) in (1), we get y = 39
Hence, the numbers are 13 and 39.
(ii) The larger of two supplementary angles exceeds the smaller by 18 degrees. Find them.
Sol: Let the larger angle by xo and smaller angle be yo.
We know that the sum of two supplementary pair of angles is always 180o.
According to the question,
x + y = 180o……………. (1)
x – y = 18o ……………..(2)
From (1), we get x = 180o – y …………. (3)
Substituting (3) in (2), we get
180o – y – y =18o
162o = 2y
y = 81o ………….. (4)
Using the value of y in (3), we get
x = 180o – 81o
= 99o
Hence, the angles are 99o and 81o.
(iii) The coach of a cricket team buys 7 bats and 6 balls for Rs.3800. Later, she buys 3 bats and 5 balls for Rs.1750. Find the cost of each bat and each ball.
Sol: Let the cost a bat be x and cost of a ball be y.
According to the question,
7x + 6y = 3800 ………………. (I)
3x + 5y = 1750 ………………. (II)
From (I), we get
y = (3800-7x)/6………………..(III)
Substituting (III) in (II). we get,
3x+5(3800-7x)/6 =1750
⇒ 3x+ 9500/3 – 35x/6 = 1750
⇒ 3x- 35x/6 = 1750 – 9500/3
⇒ (18x-35x)/6 = (5250 – 9500)/3
⇒-17x/6 = -4250/3
⇒-17x = -8500
x = 500 ……………………….. (IV)
Substituting the value of x in (III), we get
y = (3800-7 ×500)/6 = 300/6 = 50
Hence, the cost of a bat is Rs 500 and cost of a ball is Rs 50.
(iv) The taxi charges in a city consist of a fixed charge together with the charge for the distance covered. For a distance of 10 km, the charge paid is Rs 105 and for a journey of 15 km, the charge paid is Rs 155. What are the fixed charges and the charge per km? How much does a person have to pay for travelling a distance of 25 km?
Sol: Let the fixed charge be Rs x and per km charge be Rs y.
According to the question,
x + 10y = 105 …………….. (1)
x + 15y = 155 …………….. (2)
From (1), we get x = 105 – 10y ………………. (3)
Substituting the value of x in (2), we get
105 – 10y + 15y = 155
5y = 50
y = 10 …………….. (4)
Putting the value of y in (3), we get
x = 105 – 10 × 10 = 5
Hence, fixed charge is Rs 5 and per km charge = Rs 10
Charge for 25 km = x + 25y = 5 + 250 = Rs 255
(v) A fraction becomes 9/11 , if 2 is added to both the numerator and the denominator. If, 3 is added to both the numerator and the denominator it becomes 5/6. Find the fraction.
Sol: Let the fraction be x/y.
According to the question,
(x+2) /(y+2) = 9/11
11x + 22 = 9y + 18
11x – 9y = -4 …………….. (1)
(x+3) /(y+3) = 5/6
6x + 18 = 5y +15
6x – 5y = -3 ………………. (2)
From (1), we get x = (-4+9y)/11 …………….. (3)
Substituting the value of x in (2), we get
6(-4+9y)/11 -5y = -3
-24 + 54y – 55y = -33
-y = -9
y = 9 ………………… (4)
Substituting the value of y in (3), we get
x = (-4+9×9 )/11 = 7
Hence the fraction is 7/9.
(vi) Five years hence, the age of Jacob will be three times that of his son. Five years ago, Jacob’s age was seven times that of his son. What are their present ages?
Solutions: Let the age of Jacob and his son be x and y respectively.
According to the question,
(x + 5) = 3(y + 5)
x – 3y = 10 …………………………………….. (1)
(x – 5) = 7(y – 5)
x – 7y = -30 ………………………………………. (2)
From (1), we get x = 3y + 10 ……………………. (3)
Substituting the value of x in (2), we get
3y + 10 – 7y = -30
-4y = -40
y = 10 ………………… (4)
Substituting the value of y in (3), we get
x = 3 x 10 + 10 = 40
Hence, the present age of Jacob’s and his son is 40 years and 10 years respectively.
Exercise 3.3
Q1. Solve the following pair of linear equations by the elimination method and the substitution method:
(i) x + y = 5 and 2x – 3y = 4
(ii) 3x + 4y = 10 and 2x – 2y = 2
(iii) 3x – 5y – 4 = 0 and 9x = 2y + 7
(iv) x / 2 + 2y / 3 = -1 and x - y / 3 = 3
Sol: (i) x + y = 5 and 2x – 3y = 4
By the method of elimination:
x + y = 5 ……………………(i)
2x – 3y = 4 …………………(ii)
When the equation (i) is multiplied by 2, we get
2x + 2y = 10 ………………(iii)
When the equation (ii) is subtracted from (iii) we get,
5y = 6
y = 6 / 5 ………………(iv)
Substituting the value of y in eq. (i) we get,
x = 5 − 6 / 5 = 19 / 5
∴ x = 19 / 5, y = 6 / 5
By the method of substitution:
From the equation (i), we get:
x = 5 – y………………(v)
When the value is put in equation (ii) we get,
2(5 – y) – 3y = 4
-5y = -6
y = 6 / 5
When the values are substituted in equation (v), we get:
x = 5 − 6 / 5 = 19 / 5
∴ x = 19 / 5 ,y = 6 / 5
(ii) 3x + 4y = 10 and 2x – 2y = 2
By the method of elimination:
3x + 4y = 10………………(i)
2x – 2y = 2 …………………(ii)
When the equation (i) and (ii) is multiplied by 2, we get:
4x – 4y = 4 …………………(iii)
When the Equation (i) and (iii) are added, we get:
7x = 14
x = 2 ………………….(iv)
Substituting equation (iv) in (i) we get,
6 + 4y = 10
4y = 4
y = 1
Hence, x = 2 and y = 1
By the method of Substitution:
From equation (ii) we get,
x = 1 + y……………………(v)
Substituting equation (v) in equation (i) we get,
3(1 + y) + 4y = 10
7y = 7
y = 1
When y = 1 is substituted in equation (v) we get,
A = 1 + 1 = 2
Therefore, A = 2 and B = 1
(iii) 3x – 5y – 4 = 0 and 9x = 2y + 7
By the method of elimination:
3x – 5y – 4 = 0 ………………………(i)
9x = 2y + 7
9x – 2y – 7 = 0 ………………………(ii)
When the equation (i) and (iii) is multiplied we get,
9x – 15y – 12 = 0 ……………………(iii)
When the equation (iii) is subtracted from equation (ii) we get,
13y = -5
y = -5 / 13 …………………………(iv)
When equation (iv) is substituted in equation (i) we get,
3x + 25 / 13 − 4 = 0
3x = 27 / 13
x = 9 / 13
∴ x = 9 / 13 and y = -5 / 13
By the method of Substitution:
From the equation (i) we get,
x = (5y + 4) / 3 …………………………(v)
Putting the value (v) in equation (ii) we get,
9(5y + 4) / 3 − 2y − 7 = 0
13y = -5
y = -5 / 13
Substituting this value in equation (v) we get,
x = (5(-5 / 13) + 4) / 3
x = 9 / 13
∴ x = 9 / 13, y = -5 / 13
(iv) x / 2 + 2y / 3 = -1 and x - y / 3 = 3
By the method of Elimination:
3x + 4y = -6 …………………………. (i)
x - y / 3 = 3
3x – y = 9 ……………………………. (ii)
When the equation (ii) is subtracted from equation (i) we get,
5y = -15
y = - 3 ……………………….(iii)
When the equation (iii) is substituted in (i) we get,
3x – 12 = -6
3x = 6
x = 2
Hence, x = 2 , y = -3
By the method of Substitution:
From the equation (ii) we get,
x = (y + 9) / 3…………………………(v)
Putting the value obtained from equation (v) in equation (i) we get,
3(y + 9) / 3 + 4y = −6
5y = -15
y = -3
When y = -3 is substituted in equation (v) we get,
x = (-3 + 9) / 3 = 2
Therefore, x = 2 and y = -3
Q.2. Form the pair of linear equations in the following problems, and find their solutions (if they exist) by the elimination method:
(i) If we add 1 to the numerator and subtract 1 from the denominator, a fraction reduces to 1. It becomes if we only add 1 to the denominator. What is the fraction?
Sol: Let the fraction be a / b
According to the given information,
(a + 1) / (b - 1) = 1
=> a – b = -2 ……………..(i)
a / (b + 1) = 1 / 2
=> 2a - b = 1……………………(ii)
When equation (i) is subtracted from equation (ii) we get,
a = 3 ………………….(iii)
When a = 3 is substituted in equation (i) we get,
3 – b = -2
-b = -5
b = 5
Hence, the fraction is 3 / 5.
(ii) Five years ago, Nuri was thrice as old as Sonu. Ten years later, Nuri will be twice as old as Sonu. How old are Nuri and Sonu?
Sol: Let us assume, present age of Nuri is x
And present age of Sonu is y.
According to the given condition, we can write as;
x – 5 = 3(y – 5)
x – 3y = -10………………………(1)
Now, x + 10 = 2(y +10)
x – 2y = 10…………………(2)
Subtract eq. 1 from 2, to get, y = 20 …………………………(3)
Substituting the value of y in eq.1, we get,
x – 3.20 = -10
x – 60 = -10
x = 50
Therefore,
Age of Nuri is 50 years
Age of Sonu is 20 years.
(iii) The sum of the digits of a two-digit number is 9. Also, nine times this number is twice the number obtained by reversing the order of the digits. Find the number.
Sol: Let the unit digit and tens digit of a number be x and y respectively.
Then, Number (n) = 10B + A
N after reversing order of the digits = 10A + B
According to the given information, A + B = 9…………………….(i)
9(10B + A) = 2(10A + B)
88 B – 11 A = 0 -A + 8B = 0 ……………………(ii)
Adding the equations (i) and (ii) we get,
9B = 9
B = 1……………………………(3)
Substituting this value of B, in the equation (i) we get A= 8
Hence the number (N) is 10B + A = 10 x 1 + 8 = 18
(iv) Meena went to a bank to withdraw Rs.2000. She asked the cashier to give her Rs.50 and Rs.100 notes only. Meena got 25 notes in all. Find how many notes of Rs.50 and Rs.100 she received.
Sol: Let the number of Rs.50 notes be A and the number of Rs.100 notes be B
According to the given information,
A + B = 25 …………………(i)
50A + 100B = 2000 ……………………(ii)
When equation (i) is multiplied with (ii) we get,
50A + 50B = 1250 ……………………(iii)
Subtracting the equation (iii) from the equation (ii) we get,
50B = 750
B = 15
Substituting in the equation (i) we get,
A = 10
Hence, Meena has 10 notes of Rs.50 and 15 notes of Rs.100.
(v) A lending library has a fixed charge for the first three days and an additional charge for each day thereafter. Saritha paid Rs.27 for a book kept for seven days, while Susy paid Rs.21 for the book she kept for five days. Find the fixed charge and the charge for each extra day.
Sol: Let the fixed charge for the first three days be Rs.A and the charge for each day extra be Rs.B.
According to the information given,
A + 4B = 27 …………………… (i)
A + 2B = 21 ………………………(ii)
When equation (ii) is subtracted from equation (i) we get,
2B = 6
B = 3 …………………(iii)
Substituting B = 3 in equation (i) we get,
A + 12 = 27
A = 15
Hence, the fixed charge is Rs.15
And the Charge per day is Rs.3
|
126 videos|457 docs|75 tests
|
FAQs on NCERT Solutions for Class 10 Maths Chapter 3 - Pair of Linear Equations in Two Variables (Exercise 3.1)
| 1. What are the methods to solve a pair of linear equations in two variables? |  |
| 2. How do you represent a pair of linear equations graphically? |  |
| 3. What is the significance of the solution of a pair of linear equations? |  |
| 4. Can a pair of linear equations have no solution? If yes, under what conditions? |  |
| 5. How can you verify if a solution to a pair of linear equations is correct? |  |























