NCERT Solutions for Class 10 Maths Chapter 4 - Quadratic Equations (Exercise 4.1)
Exercise 4.1

Q1. Check whether the following are quadratic equations:
(i) (x + 1)2 = 2(x−3)
We have:
(x + 1)2 = 2 (x − 3)
⇒ x2 + 2x + 1 = 2x − 6
⇒ x2 + 2x + 1 − 2x + 6 = 0
⇒ x2 + 7 = 0
On comparing x2 + 7 to ax2 + bx+ c=0 we find x2 + 7 = 0 is a quadratic polynomial
∴ (x + 1)2 = 2(x − 3) is a quadratic equation.
(ii) x2−2x = (− 2) (3 −x)
We have:
x2 − 2x = (− 2) (3 − x)
⇒ x2 − 2x = − 6 + 2x
⇒ x2 − 2x − 2x + 6 = 0
⇒ x2 − 4x + 6 = 0
On comparing x2 − 4x + 6 to ax2 + bx+ c=0 we find x2 − 4x + 6 is a quadratic polynomial
Since x2 − 4x + 6 is a quadratic polynomial
∴ x2 − 2x = (−2) (3 − x) is a quadratic equation.
(iii) (x−2) (x + 1) = (x−1) (x + 3)
We have:
(x − 2) (x + 1) = (x − 1) (x + 3)
⇒ x2 − x − 2 = x2 + 2x − 3
⇒ x2 − x − 2 − x2 − 2x + 3 = 0
⇒ −3x + 1 = 0
On comparing −3x + 1 = 0 to ax2 + bx+ c=0 we find −3x + 1 = 0 is not a quadratic polynomial
Since −3x + 1 is a linear polynomial
∴ (x − 2) (x + 1) = (x − 1) (x + 3) is not quadratic equation.
(iv) (x−3) (2x + 1) = x(x + 5)
We have:
(x − 3) (2x + 1) = x (x + 5)
⇒ 2x2 + x − 6x −3 = x2 + 5x
⇒ 2x2 − 5x − 3 − x2 − 5x = 0
⇒ x2 - 10x − 3 = 0
On comparing x2 - 10x − 3= 0 to ax2 + bx+ c=0 we find x2 - 10x − 3= 0 is a quadratic polynomial
Since x2 - 10x − 3 is a quadratic polynomial
∴ (x − 3) (2x + 1) = x(x + 5) is a quadratic equation.
(v) (2x−1) (x−3) = (x + 5) (x−1)
We have:
(2x − 1) (x − 3) = (x + 5) (x − 1)
⇒ 2x2 − 6x − x + 3 = x2 − x + 5x − 5
⇒ 2x2 − x2 − 6x − x + x − 5x + 3 + 5 = 0
⇒ x2 − 11x + 8 = 0
On comparing to x2 − 11x + 8 = 0 to ax2 + bx+ c=0, we find x2 − 11x + 8 = 0 is a quadratic polynomial
Since x2 − 11x + 8 is a quadratic polynomial
∴ (2x − 1) (x − 3) = (x + 5) (x − 1) is a quadratic equation.
(vi) x2 + 3x + 1 = (x−2)2
We have:
x2 + 3x + 1 = (x − 2)2
⇒ x2 + 3x + 1 = x2 − 4x + 4
⇒ x2 + 3x + 1 − x2 + 4x −4= 0
⇒ 7x − 3 = 0
On comparing 7x − 3 = 0 to ax2 + bx+ c=0 we find 7x − 3 = 0 is a quadratic polynomial
Since 7x − 3 is a linear polynomial
∴ x2 + 3x + 1 = (x − 2)2 is not a quadratic equation.
(vii) (x + 2)3 = 2x(x2−1)
We have:
(x + 2)3 = 2x(x2 − 1)
⇒ x3 + 3x2(2) + 3x(2)2 + (2)3 = 2x3 − 2x
⇒ x3 + 6x2 + 12x + 8 = 2x3 − 2x
⇒ x3 + 6x2 + 12x + 8 − 2x3 + 2x = 0
⇒− x3 + 6x2 + 14x + 8 = 0
On comparing− x3 + 6x2 + 14x + 8 = 0 to ax2 + bx+ c=0 we find − x3 + 6x2 + 14x + 8 = 0 is NOT a quadratic polynomial
Since −x3 + 6x2 + 14x + 8 is a polynomial of degree 3
∴ (x + 2)3 = 2x(x2 − 1) is not a quadratic equation.
(viii) x3−4x2−x + 1 = (x− 2)3
We have:
x3 − 4x2 − x + 1 = (x − 2)3
⇒ x3 − 4x2 − x + 1 = x3 + 3x2(− 2) + 3x(− 2)2 + (− 2)3
⇒ x3 − 4x2 − x + 1 = x3 − 6x2 + 12x − 8
⇒ x3 − 4x2 − x − 1 − x3 + 6x2 − 12x + 8 = 0
⇒ 2x2 − 13x + 9 = 0
On comparing 2x2 − 13x + 9 = 0 to ax2 + bx+ c=0 we find 2x2 − 13x + 9 = 0 is a quadratic polynomial
Since 2x2 − 13x + 9 is a quadratic polynomial
∴ x3 − 4x2 − x + 1 = (x − 2)3 is a quadratic equation.
Q2. Represent the following situations in the form of quadratic equations:
(i) The area of a rectangular plot is 528 m2. The length of the plot (in metres) is one more than twice its breadth. We need to find the length and breadth of the plot.
Let the breadth = x metres
∵ Length = 2 (Breadth) + 1
∴ Length = (2x + 1) metres
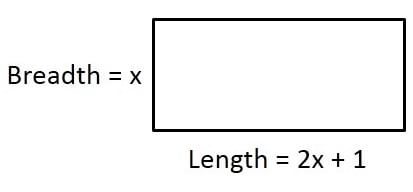
Since Length × Breadth = Area
∴ (2x + 1) × x = 528
⇒ 2x2 + x = 528
⇒ 2x2 + x − 528 = 0
Thus, the required quadratic equation is 2x2 + x− 528 = 0
(ii) The product of two consecutive positive integers is 306. We need to find the integers.
Let the two consecutive numbers be x and (x + 1).
∵Product of the numbers = 306
∴ x (x + 1) = 306
⇒ x2 + x = 306
⇒ x2 + x − 306 = 0
Thus, the required quadratic equation is x2 + x − 306 = 0
(iii) Rohan’s mother is 26 years older than him. The product of their ages (in years) 3 years from now will be 360. We would like to find Rohan’s present age.
Let the present age = x
∴ Mother’s age = (x + 26) years
After 3 years
His age = (x + 3) years
Mother’s age = [(x + 26) + 3] years
=(x + 29) years
According to the condition,
⇒ (x + 3) × (x + 29) = 360
⇒ x(x+29) + 3(x+29) = 360
⇒ x2 + 29x + 3x + 87 = 360
⇒ x2 + 29x + 3x + 87 − 360 = 0
⇒ x2 + 32x − 273 = 0
Thus, the required quadratic equation is x2 + 32x − 273 = 0
(iv) A train travels a distance of 480 km at a uniform speed. If the speed had been 8 km/h less, then it would have taken 3 hours more to cover the same distance. We need to find the speed of the train.
In the first case,
Let the speed of the train = u km/hr
Distance covered = 480 km
Time taken = Distance ÷ Speed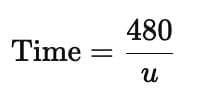
In the second case,
Speed = (u − 8) km/hour
According to the condition,
⇒ 480u − 480(u − 8) = 3u(u − 8)
⇒ 480u − 480u + 3840 = 3u2 − 24u
⇒ 3840 − 3u2 + 24u =0
⇒ 1280 − u2 + 8u =0
⇒ − 1280 + u2 − 8u =0
⇒ u2 − 8u − 1280 = 0
Thus, the required quadratic equation is u2 − 8u – 1280 = 0
Exercise 4.2
 FactorisationQ1. Find the roots of the following quadratic equations by factorisation:
FactorisationQ1. Find the roots of the following quadratic equations by factorisation:
Solutions:
(i) x2 – 3x – 10 = 0
Taking LHS,
⇒x2 – 5x + 2x – 10
⇒x(x – 5) + 2(x – 5)
⇒(x – 5)(x + 2)
The roots of this equation, x2 – 3x – 10 = 0 are the values of x for which (x – 5)(x + 2) = 0
Therefore, x – 5 = 0 or x + 2 = 0
⇒ x = 5 or x = -2
(ii) 2x2 + x – 6 = 0
Taking LHS,
⇒ 2x2 + 4x – 3x – 6
⇒ 2x(x + 2) – 3(x + 2)
⇒ (x + 2)(2x – 3)
The roots of this equation, 2x2 + x – 6=0 are the values of x for which (x – 5)(x + 2) = 0
Therefore, x + 2 = 0 or 2x – 3 = 0
⇒ x = -2 or x = 3/2
(iii) √2 x2 + 7x + 5√2 = 0
Taking LHS,
⇒ √2 x2 + 5x + 2x + 5√2
⇒ x (√2x + 5) + √2(√2x + 5)= (√2x + 5)(x + √2)
The roots of this equation, √2 x2 + 7x + 5√2=0 are the values of x for which (x – 5)(x + 2) = 0
Therefore, √2x + 5 = 0 or x + √2 = 0
⇒ x = -5/√2 or x = -√2
(iv) 2x2 – x +1/8 = 0
Taking LHS,
⇒1/8 (16x2 – 8x + 1)
⇒ 1/8 (16x2 – 4x -4x + 1)
⇒1/8 (4x(4x – 1) -1(4x – 1))
⇒1/8 (4x – 1)2
The roots of this equation, 2x2 – x + 1/8 = 0, are the values of x for which (4x – 1)2= 0
Therefore, (4x – 1) = 0 or (4x – 1) = 0
⇒ x = 1/4
(v) Given, 100x2 – 20x + 1=0
Taking LHS,
⇒100x2 – 10x – 10x + 1
⇒10x(10x – 1) -1(10x – 1)
⇒(10x – 1)2
The roots of this equation, 100x2 – 20x + 1=0, are the values of x for which (10x – 1)2= 0
∴ (10x – 1) = 0 or (10x – 1) = 0
⇒x = 1/10
Q2. Solve the problems given in Example 1.
Represent the following situations mathematically:
(i) John and Jivanti together have 45 marbles. Both of them lost 5 marbles each, and the product of the number of marbles they now have is 124. We would like to find out how many marbles they had to start with.
(ii) A cottage industry produces a certain number of toys in a day. The cost of production of each toy (in rupees) was found to be 55 minus the number of toys produced in a day. On a particular day, the total cost of production was Rs 750. We would like to find out the number of toys produced on that day.
Solutions:
(i) Let us say, the number of marbles John has = x.
Therefore, the number of marble Jivanti have = 45 – x
After losing 5 marbles each,
Number of marbles John have = x – 5
Number of marble Jivanti have = 45 – x – 5 = 40 – x
Given that the product of their marbles is 124.
∴ (x – 5)(40 – x) = 124
⇒ x2 – 45x + 324 = 0
⇒ x2 – 36x – 9x + 324 = 0
⇒ x(x – 36) -9(x – 36) = 0
⇒ (x – 36)(x – 9) = 0
Thus, we can say,
x – 36 = 0 or x – 9 = 0
⇒ x = 36 or x = 9
Therefore,
If, John’s marbles = 36,
Then, Jivanti’s marbles = 45 – 36 = 9
And if John’s marbles = 9,
Then, Jivanti’s marbles = 45 – 9 = 36
(ii) Let us say, the number of toys produced in a day is x.
Therefore, cost of production of each toy = Rs(55 – x)
Given, the total cost of production of the toys = Rs 750
∴ x(55 – x) = 750
⇒ x2 – 55x + 750 = 0
⇒ x2 – 25x – 30x + 750 = 0
⇒ x(x – 25) -30(x – 25) = 0
⇒ (x – 25)(x – 30) = 0
Thus, either x -25 = 0 or x – 30 = 0
⇒ x = 25 or x = 30
Hence, the number of toys produced in a day, will be either 25 or 30.
Q3. Find two numbers whose sum is 27 and product is 182.
Solution:
Let us say, first number be x and the second number is 27 – x.
Therefore, the product of two numbers
x(27 – x) = 182
⇒ x2 – 27x – 182 = 0
⇒ x2 – 13x – 14x -182 = 0
⇒ x(x – 13) -14(x – 13) = 0
⇒ (x – 13)(x -14) = 0
Thus, either, x = -13 = 0 or x – 14 = 0
⇒ x = 13 or x = 14
Therefore, if first number = 13, then second number = 27 – 13 = 14
And if first number = 14, then second number = 27 – 14 = 13
Hence, the numbers are 13 and 14.
Q4. Find two consecutive positive integers, sum of whose squares is 365.
Solution:
Let us say, the two consecutive positive integers be x and x + 1.
Therefore, as per the given questions,
x2 + (x + 1)2 = 365
⇒ x2 + x2 + 1 + 2x = 365
⇒ 2x2 + 2x – 364 = 0
⇒ x2 + x – 182 = 0
⇒ x2 + 14x – 13x – 182 = 0
⇒ x(x + 14) -13(x + 14) = 0
⇒ (x + 14)(x – 13) = 0
Thus, either, x + 14 = 0 or x – 13 = 0,
⇒ x = – 14 or x = 13
since, the integers are positive, x can be 13, only.
∴ x + 1 = 13 + 1 = 14
Therefore, two consecutive positive integers will be 13 and 14.
Q5. The altitude of a right triangle is 7 cm less than its base. If the hypotenuse is 13 cm, find the other two sides.
Solution:
Let us say, the base of the right triangle be x cm.
Given, the altitude of right triangle = (x – 7) cm
From Pythagoras theorem, we know,
Base2 + Altitude2 = Hypotenuse2
∴ x2 + (x – 7)2 = 132
⇒ x2 + x2 + 49 – 14x = 169
⇒ 2x2 – 14x – 120 = 0
⇒ x2 – 7x – 60 = 0
⇒ x2 – 12x + 5x – 60 = 0
⇒ x(x – 12) + 5(x – 12) = 0
⇒ (x – 12)(x + 5) = 0
Thus, either x – 12 = 0 or x + 5 = 0,
⇒ x = 12 or x = – 5
Since sides cannot be negative, x can only be 12.
Hence, the base of the given triangle is 12 cm and the altitude of this triangle will be (12 – 7) cm = 5 cm.
Q6. A cottage industry produces a certain number of pottery articles in a day. It was observed on a particular day that the cost of production of each article (in rupees) was 3 more than twice the number of articles produced on that day. If the total cost of production on that day was Rs.90, find the number of articles produced and the cost of each article.
Solution:
Let us say, the number of articles produced is x.
Therefore, cost of production of each article = Rs (2x + 3)
Given, the total cost of production is Rs.90
∴ x(2x + 3) = 90
⇒ 2x2 + 3x – 90 = 0
⇒ 2x2 + 15x -12x – 90 = 0
⇒ x(2x + 15) -6(2x + 15) = 0
⇒ (2x + 15)(x – 6) = 0
Thus, either 2x + 15 = 0 or x – 6 = 0
⇒ x = -15/2 or x = 6
As the number of articles produced can only be a positive integer, therefore, x can only be 6.
Hence, the number of articles produced = 6
Cost of each article = 2 × 6 + 3 = Rs 15.
Exercise 4.3
Q1. Find the nature of the roots of the following quadratic equations. If the real roots exist, find them;
(i) 2x2 – 3x + 5 = 0
(ii) 3x2 – 4√3x + 4 = 0
(iii) 2x2 – 6x + 3 = 0
Solutions:
(i) Given,
2x2 – 3x + 5 = 0
Comparing the equation with ax2 + bx + c = 0, we get
a = 2, b = -3 and c = 5
We know, Discriminant = b2 – 4ac
= ( – 3)2 – 4 (2) (5) = 9 – 40
= – 31
As you can see, b2 – 4ac < 0
Therefore, no real root is possible for the given equation, 2x2 – 3x + 5 = 0.
(ii) 3x2 – 4√3x + 4 = 0
Comparing the equation with ax2 + bx + c = 0, we get
a = 3, b = -4√3 and c = 4
We know, Discriminant = b2 – 4ac
= (-4√3)2 – 4(3)(4)
= 48 – 48 = 0
As b2 – 4ac = 0,
Real roots exist for the given equation and they are equal to each other.
Hence the roots will be –b/2a and –b/2a.
–b/2a = -(-4√3)/2×3 = 4√3/6 = 2√3/3 = 2/√3
Therefore, the roots are 2/√3 and 2/√3.
(iii) 2x2 – 6x + 3 = 0
Comparing the equation with ax2 + bx + c = 0, we get
a = 2, b = -6, c = 3
As we know, Discriminant = b2 – 4ac
= (-6)2 – 4 (2) (3)
= 36 – 24 = 12
As b2 – 4ac > 0,
Therefore, there are distinct real roots exist for this equation, 2x2 – 6x + 3 = 0.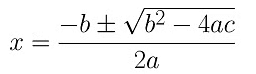 = (-(-6) ± √(-62-4(2)(3)) )/ 2(2)
= (-(-6) ± √(-62-4(2)(3)) )/ 2(2)
= (6±2√3 )/4
= (3±√3)/2
Therefore the roots for the given equation are (3+√3)/2 and (3-√3)/2
Q2. Find the values of k for each of the following quadratic equations, so that they have two equal roots.
(i) 2x2 + kx + 3 = 0
(ii) kx (x – 2) + 6 = 0
Solutions:
(i) 2x2+ kx + 3 = 0
Comparing the given equation with ax2 + bx + c = 0, we get,
a = 2, b = k and c = 3
As we know, Discriminant = b2 – 4ac
= (k)2 – 4(2) (3)
= k2 – 24
For equal roots, we know,
Discriminant = 0
k2 – 24 = 0
k2 = 24
k = ±√24 = ±2√6
(ii) kx(x – 2) + 6 = 0
or kx2 – 2kx + 6 = 0
Comparing the given equation with ax2 + bx + c = 0, we get
a = k, b = – 2k and c = 6
We know, Discriminant = b2 – 4ac
= ( – 2k)2 – 4 (k) (6)
= 4k2 – 24k
For equal roots, we know,
b2 – 4ac = 0
4k2 – 24k = 0
4k (k – 6) = 0
Either 4k = 0 or k = 6 = 0
k = 0 or k = 6
However, if k = 0, then the equation will not have the terms ‘x² ‘ and ‘x‘.
Therefore, if this equation has two equal roots, k should be 6 only.
Q3. Is it possible to design a rectangular mango grove whose length is twice its breadth, and the area is 800 m2? If so, find its length and breadth.
Solution:
Let the breadth of mango grove be l.
Length of mango grove will be 2l.
Area of mango grove = (2l) (l)= 2l2
2l2 = 800
l2 = 800/2 = 400
l2 – 400 =0
Comparing the given equation with ax2 + bx + c = 0, we get
a = 1, b = 0, c = 400
As we know, Discriminant = b2 – 4ac
=> (0)2 – 4 × (1) × ( – 400) = 1600
Here, b2 – 4ac > 0
Thus, the equation will have real roots. And hence, the desired rectangular mango grove can be designed.
l = ±20
As we know, the value of length cannot be negative.
Therefore, breadth of mango grove = 20 m
Length of mango grove = 2 × 20 = 40 m
Q4. Is the following situation possible? If so, determine their present ages. The sum of the ages of two friends is 20 years. Four years ago, the product of their ages in years was 48.
Solution:
Let’s say, the age of one friend be x years.
Then, the age of the other friend will be (20 – x) years.
Four years ago,
Age of First friend = (x – 4) years
Age of Second friend = (20 – x – 4) = (16 – x) years
As per the given question, we can write,
(x – 4) (16 – x) = 48
16x – x2 – 64 + 4x = 48
– x2 + 20x – 112 = 0
x2 – 20x + 112 = 0
Comparing the equation with ax2 + bx + c = 0, we get
a = 1, b = -20 and c = 112
Discriminant = b2 – 4ac
= (-20)2 – 4 × 112
= 400 – 448 = -48
b2 – 4ac < 0
Therefore, there will be no real solution possible for the equations. Hence, condition doesn’t exist.
Q5. Is it possible to design a rectangular park of perimeter 80 and area 400 m2? If so find its length and breadth.
Solution:
Let the length and breadth of the park be l and b.
Perimeter of the rectangular park = 2 (l + b) = 80
So, l + b = 40
Or, b = 40 – l
Area of the rectangular park = l×b = l(40 – l) = 40l – l2 = 400
l2 – 40l + 400 = 0, which is a quadratic equation.
Comparing the equation with ax2 + bx + c = 0, we get
a = 1, b = -40, c = 400
Since, Discriminant = b2 – 4ac
=(-40)2 – 4 × 400
= 1600 – 1600 = 0
Thus, b2 – 4ac = 0
Therefore, this equation has equal real roots. Hence, the situation is possible.
Root of the equation,
l = –b/2a
l = (40)/2(1) = 40/2 = 20
Therefore, length of rectangular park, l = 20 m
And breadth of the park, b = 40 – l = 40 – 20 = 20 m.
|
127 videos|584 docs|79 tests
|
FAQs on NCERT Solutions for Class 10 Maths Chapter 4 - Quadratic Equations (Exercise 4.1)
| 1. What is a quadratic equation? |  |
| 2. How can I solve a quadratic equation using the quadratic formula? |  |
| 3. What is the discriminant in a quadratic equation, and what does it indicate? |  |
| 4. Can quadratic equations have complex roots? |  |
| 5. What are some real-life applications of quadratic equations? |  |

















