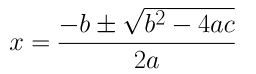Q1. Find the nature of the roots of the following quadratic equations. If the real roots exist, find them;
(i) 2x2 – 3x + 5 = 0
(ii) 3x2 – 4√3x + 4 = 0
(iii) 2x2 – 6x + 3 = 0
Solutions:
(i) Given,
2x2 – 3x + 5 = 0
Comparing the equation with ax2 + bx + c = 0, we get
a = 2, b = -3 and c = 5
We know, Discriminant = b2 – 4ac
= ( – 3)2 – 4 (2) (5) = 9 – 40
= – 31
As you can see, b2 – 4ac < 0
Therefore, no real root is possible for the given equation, 2x2 – 3x + 5 = 0.
(ii) 3x2 – 4√3x + 4 = 0
Comparing the equation with ax2 + bx + c = 0, we get
a = 3, b = -4√3 and c = 4
We know, Discriminant = b2 – 4ac
= (-4√3)2 – 4(3)(4)
= 48 – 48 = 0
As b2 – 4ac = 0,
Real roots exist for the given equation and they are equal to each other.
Hence the roots will be –b/2a and –b/2a.
–b/2a = -(-4√3)/2×3 = 4√3/6 = 2√3/3 = 2/√3
Therefore, the roots are 2/√3 and 2/√3.
(iii) 2x2 – 6x + 3 = 0
Comparing the equation with ax2 + bx + c = 0, we get
a = 2, b = -6, c = 3
As we know, Discriminant = b2 – 4ac
= (-6)2 – 4 (2) (3)
= 36 – 24 = 12
As b2 – 4ac > 0,
Therefore, there are distinct real roots exist for this equation, 2x2 – 6x + 3 = 0.
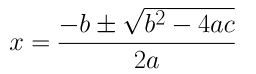
= (-(-6) ± √(-62-4(2)(3)) )/ 2(2)
= (6±2√3 )/4
= (3±√3)/2
Therefore the roots for the given equation are (3+√3)/2 and (3-√3)/2
Q2. Find the values of k for each of the following quadratic equations, so that they have two equal roots.
(i) 2x2 + kx + 3 = 0
(ii) kx (x – 2) + 6 = 0
Solutions:
(i) 2x2 + kx + 3 = 0
Comparing the given equation with ax2 + bx + c = 0, we get,
a = 2, b = k and c = 3
As we know, Discriminant = b2 – 4ac
= (k)2 – 4(2) (3)
= k2 – 24
For equal roots, we know,
Discriminant = 0
k2 – 24 = 0
k2 = 24
k = ±√24 = ±2√6
(ii) kx(x – 2) + 6 = 0
or kx2 – 2kx + 6 = 0
Comparing the given equation with ax2 + bx + c = 0, we get
a = k, b = – 2k and c = 6
We know, Discriminant = b2 – 4ac
= ( – 2k)2 – 4 (k) (6)
= 4k2 – 24k
For equal roots, we know,
b2 – 4ac = 0
4k2 – 24k = 0
4k (k – 6) = 0
Either 4k = 0 or k = 6 = 0
k = 0 or k = 6
However, if k = 0, then the equation will not have the terms ‘x2‘ and ‘x‘.
Therefore, if this equation has two equal roots, k should be 6 only.
Q3. Is it possible to design a rectangular mango grove whose length is twice its breadth, and the area is 800 m2? If so, find its length and breadth.
Solution:
Let the breadth of mango grove be l.
Length of mango grove will be 2l.
Area of mango grove = (2l) (l)= 2l2
2l2 = 800
l2 = 800/2 = 400
l2 – 400 =0
Comparing the given equation with ax2 + bx + c = 0, we get
a = 1, b = 0, c = 400
As we know, Discriminant = b2 – 4ac
=> (0)2 – 4 × (1) × ( – 400) = 1600
Here, b2 – 4ac > 0
Thus, the equation will have real roots. And hence, the desired rectangular mango grove can be designed.
l = ±20
As we know, the value of length cannot be negative.
Therefore, breadth of mango grove = 20 m
Length of mango grove = 2 × 20 = 40 m
Q4. Is the following situation possible? If so, determine their present ages. The sum of the ages of two friends is 20 years. Four years ago, the product of their ages in years was 48.
Solution:
Let’s say, the age of one friend be x years.
Then, the age of the other friend will be (20 – x) years.
Four years ago,
Age of First friend = (x – 4) years
Age of Second friend = (20 – x – 4) = (16 – x) years
As per the given question, we can write,
(x – 4) (16 – x) = 48
16x – x2 – 64 + 4x = 48
– x2 + 20x – 112 = 0
x2 – 20x + 112 = 0
Comparing the equation with ax2 + bx + c = 0, we get
a = 1, b = -20 and c = 112
Discriminant = b2 – 4ac
= (-20)2 – 4 × 112
= 400 – 448 = -48
b2 – 4ac < 0
Therefore, there will be no real solution possible for the equations. Hence, condition doesn’t exist.
Q5. Is it possible to design a rectangular park of perimeter 80 and area 400 m2? If so find its length and breadth.
Solution:
Let the length and breadth of the park be l and b.
Perimeter of the rectangular park = 2 (l + b) = 80
So, l + b = 40
Or, b = 40 – l
Area of the rectangular park = l×b = l(40 – l) = 40l – l2 = 400
l2 – 40l + 400 = 0, which is a quadratic equation.
Comparing the equation with ax2 + bx + c = 0, we get
a = 1, b = -40, c = 400
Since, Discriminant = b2 – 4ac
=(-40)2 – 4 × 400
= 1600 – 1600 = 0
Thus, b2 – 4ac = 0
Therefore, this equation has equal real roots. Hence, the situation is possible.
Root of the equation,
l = –b/2a
l = (40)/2(1) = 40/2 = 20
Therefore, length of rectangular park, l = 20 m
And breadth of the park, b = 40 – l = 40 – 20 = 20 m.