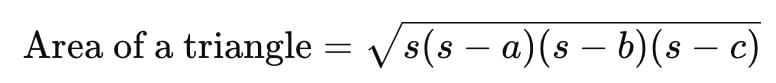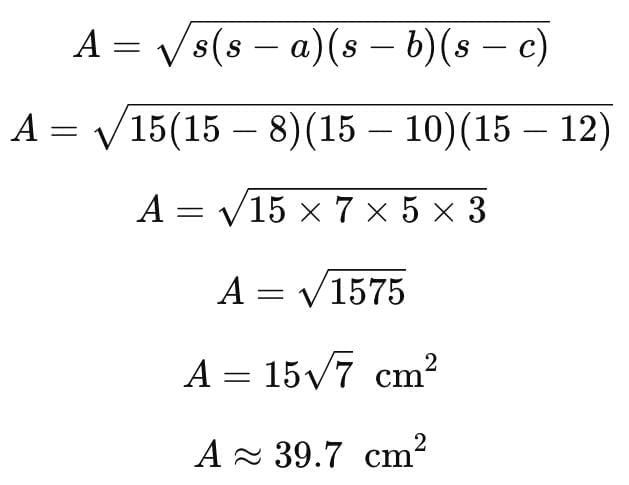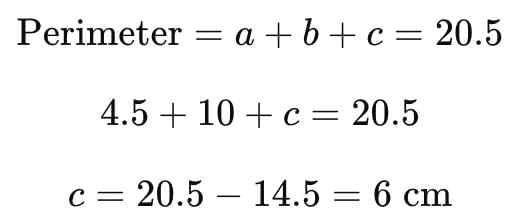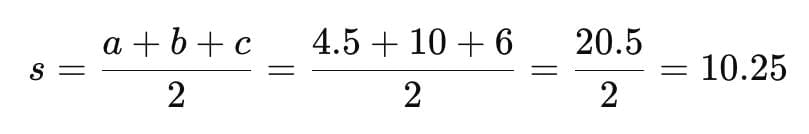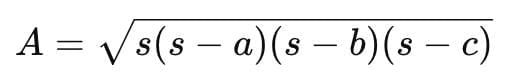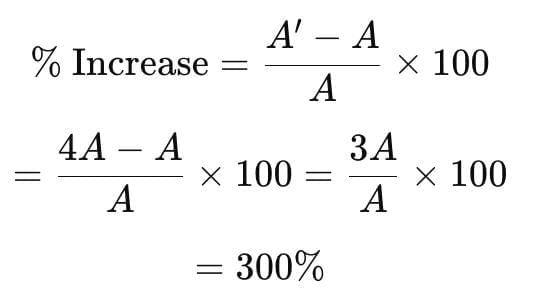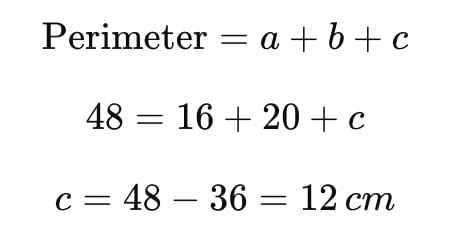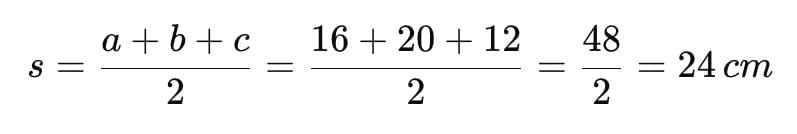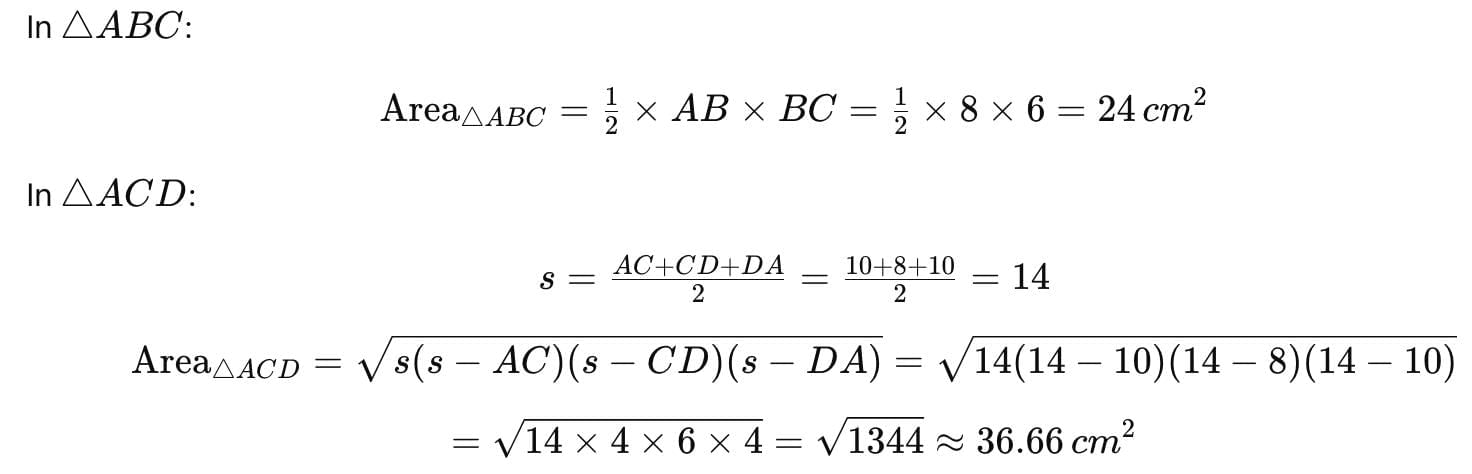Class 9 Maths Chapter 10 Question Answers - Heron’s Formula

Q1. Find the area of a triangle whose sides are 8 cm, 10 cm, and 12 cm.

Sol: Let the semi-perimeter $s$s be:

s = 8 + 10 + 122 = 15 cm

Heron's formula for the area of the triangle:

where a, b, and c are the sides of the triangle 

Substituting the values:

Area = 39.7 cm²

Q2. Find the area of a triangle whose sides are 4.5 cm and 10 cm and perimeter 20.5 cm.

Sol: Given,

Side a = 4.5 cm

Side b = 10 cm

Perimeter of triangle = 20.5 cm

Thus, the third side of the triangle is c = 6 cm

Semi perimeter (s):

Using Heron’s formula, the area is calculated as follows:

Q3. If every side of a triangle is doubled, by what percentage is the area of the triangle increased?

Sol:  Let’s solve step by step:

Sides of the original triangle = a,b,c
Area of original triangle = A

If every side is doubled, then 
New sides = $2a,\; 2b,\; 2c$2a,2b,2c

From Heron’s formula:

If each side is multiplied by 2, the new semi-perimeter also becomes twice the original value.
So, the new area =
Percentage increase:

The area increases by 300%.

Q4. A triangular field has sides 150 m, 120 m, and 100 m. A gardener has to put a fence all around it and also plant grass inside. How much area does he need to plant grass?

Sol: Given,

Sides of triangular park are 150m, 120m and 100m.

Semi perimeter (s):
Using Heron’s formula, we have;

The area that needs to be planted with grass is 5982.9 m².

Q5. Find the area of a triangle whose two sides are 16 cm and 20 cm, and the perimeter is 48 cm.

Sol: We are given two sides of a triangle: $a\; =\; 16\; \backslash ,\; cm$a=16cm, $b\; =\; 20\; \backslash ,\; cm$b=20cm, and the perimeter $=$48cm.
From this, we first find the third side.

Now, the three sides of the triangle are 16 cm, 20 cm, and 12 cm.

Semi-perimeter(s):

Area of the triangle using the Heron’s formula:

The area of the triangle is 96 cm²

Q6. The sides of a triangle are in the ratio 8: 15: 17 and its perimeter is 680 cm. Find its area.

Sol: Given:
The ratio of the sides of the triangle is given as 8:15:17.
Let the common ratio between the sides of the triangle be "x".

Thus, the sides are $8x,\; 15x,$8x, 15x, and 17x.

It is also given that the perimeter of the triangle is 680 cm:

$\hspace{0.17em}cm8x\; +\; 15x\; +\; 17x\; =\; 680\; \backslash ,\; \backslash text\{cm\}$8x + 15x + 17x = 680cm
40x = 680cm
$x\; =\; 17$x = 17
Now, the sides of the triangle are:
$\hspace{0.17em}cm8\; \backslash times\; 17\; =\; 136\; \backslash ,\; \backslash text\{cm\},\; \backslash quad\; 15\; \backslash times\; 17\; =\; 255\; \backslash ,\; \backslash text\{cm\},\; \backslash quad\; 17\; \backslash times\; 17\; =\; 289\; \backslash ,\; \backslash text\{cm\}$8 × 17 = 136cm, 15 × 17 = 255cm, 17 × 17 = 289cm
the semi-perimeter of the triangle $s=\frac{680}{2}=340\hspace{0.17em}cms\; =\; \backslash frac\{680\}\{2\}\; =\; 340\; \backslash ,\; \backslash text\{cm\}$
Using Heron's Formula:

Q7. The lengths of sides of a triangle are in the ratio 3 : 4 : 5 and its perimeter is 120 cm, find its area. 

Sol: The sides are in the ratio of 3 : 4 : 5.
Let the sides be 3x, 4x and 5x.
∴ Perimeter = 3x + 4x + 5x = 12x
Now 12x = 120                [Perimeter = 120 cm]
⇒   x =(120/12) = 10
∴ Sides of the triangle are: a = 3x = 3 x 10 = 30 cm
b = 4x = 4 x 10 = 40 cm
c = 5x = 5 x 10 = 50 cm
Now, semi-perimeter (s) = (120/12) cm = 60 cm

Using Heron’s formula, we have  
Area of the triangle:

Thus, the required area of the triangle = 600 cm².

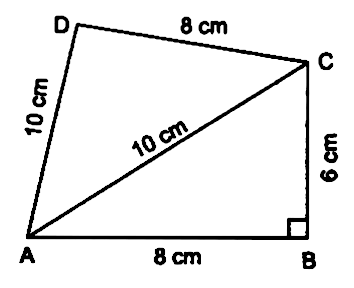
Q8. Find the area of a quadrilateral ABCD in which AB = 8 cm, BC = 6 cm, CD = 8 cm, DA = 10 cm and AC = 10 cm.

Sol: In ΔABC, ∠B = 90°

We have a quadrilateral ABCD with sides $AB\; =\; 8\; \backslash ,\; cm$AB=8cm, BC=6cm, $CD\; =\; 8\; \backslash ,\; cm$CD=8cm, $DA\; =\; 10\; \backslash ,\; cm$DA=10cm, diagonal $AC\; =\; 10\; \backslash ,\; cm$AC=10cm, and ∠B=90^.

Therefore, the total area of the quadrilateral ABCD is:

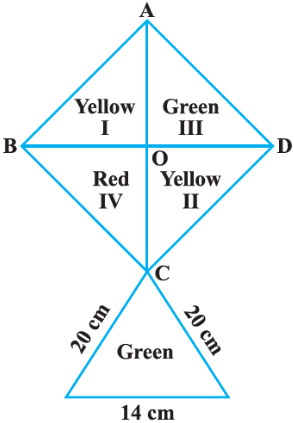
Q9. How much paper of each shade is needed to make a kite given in the figure, in which ABCD is a square of diagonal 44 cm.

Sol: The diagonals of a square bisect each other at right angles

ABCD is a square with a diagonal of 44 cm.

Area of square = ½ × (diagonal)²
= ½ × 44²
= ½ × 1936
= 968 cm²

The diagonals of the square bisect each other at right angles, so the square is divided into four equal triangles.
Each triangle = 968 ÷ 4 = 242 cm²

So,
Yellow I = 242 cm²
Yellow II = 242 cm²
Green III = 242 cm²
Red IV = 242 cm²

Below the square is an isosceles triangle with sides 20 cm, 20 cm, and base 14 cm.

s = (20 + 20 + 14) ÷ 2 = 27

Area using the Herons Formula:

So, the bottom Green = 131.1 cm²

Total paper needed = 968 + 131.1 = 1099.1 cm²

Answer:
Yellow I = 242 cm², Yellow II = 242 cm², Green III = 242 cm², Red IV = 242 cm², Green (bottom) = 131.1 cm².