NCERT Solutions for Class 9 Maths Chapter 11 - Surface Areas and Volumes
| Table of contents |

|
| Exercise 11.1 |

|
| Exercise 11.2 |

|
| Exercise 11.3 |

|
| Exercise 11.4 |

|
Exercise 11.1
Q1. Diameter of the base of a cone is 10.5 cm and its slant height is 10 cm. Find its curved surface area (Assume π = 22 / 7)
Ans: Radius of cone r = 10.5/2 = 5.25 cm and slant height / = 10 cm
Curved surface area of cone = πrl
= 22/7 × 5.25 × 10
= 22 × 0.75 × 10 = 165 cm2
Hence, the curved surface area of cone is 165 cm2.
Q2. Find the total surface area of a cone, if its slant height is 21 m and diameter of its base is 24 m. (Assume π = 22 / 7)
Ans:
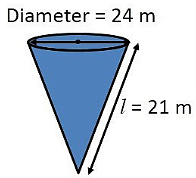 Radius (r) = 24/2 m = 12 m
Radius (r) = 24/2 m = 12 m
Slant height (l) = 21 m
Total surface area of the cone = πr (l + r) m2
= 22/7 × 12 × (21 + 12) m2
= (22/7 × 12 × 33) m2
= 1244.57 m2
Q3. Curved surface area of a cone is 308 cm2 and its slant height is 14 cm. Find
(i) radius of the base and
(ii) total surface area of the cone. (Assume π = 22 / 7)
Ans: (i) Curved surface area of cone = 308 cm2 and slant height / = 14 cm
Let, the radius of base of cone = r cm
Curved surface area of cone = πrl
⇒ 308 = 22/7 × r × 14
⇒ 308 = 44r
⇒ r = 308/44 = 7 cm
Hence, the radius of base of cone is 7 cm. (ii) Total surface area of cone = πr(r + l)
(ii) Total surface area of cone = πr(r + l)
= 22/7 × 7 × (7 + 14)
= 22 × 21 = 462 cm2
Hence, the total surface area of cone is 462 cm2.
Q4. A conical tent is 10 m high and the radius of its base is 24 m. Find
(i) slant height of the tent.
(ii) cost of the canvas required to make the tent, if the cost of 1 m2 canvas is Rs 70. (Assume π = 22 / 7)
Ans: (i) Radius of cone r = 24 m and height h = 10 m
Let, the slant height = l m
We know that, l2 = r2 + h2
⇒ l2 =242 +102 = 576 + 100 = 676
l = √676 = 26m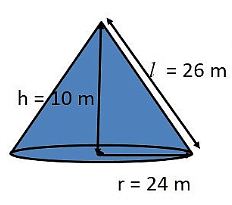 (ii) Area of canvas to make the tent = πrl
(ii) Area of canvas to make the tent = πrl
22/7 × 24 × 26 m2
Cost of 1 m2 canvas = ₹ 70
Therefore, the cost of 22/7 × 24 × 26 m2 canvas = ₹ 70 × 22/7 × 24 × 26 = ₹ 137280
Hence, the cost of canvas to make the tent is ₹ 137280.
Q5. What length of tarpaulin 3 m wide will be required to make conical tent of height 8 m and base radius 6m? Assume that the extra length of material that will be required for stitching margins and wastage in cutting is approximately 20 cm. [Use π = 3.14]
Ans: Radius of cone r = 6 m and height h = 8 m
Let, the slant height = l m
We know that, l2 = r2 + h2
⇒ l2 = 62 + 82 = 36 + 64 = 100 ⇒ l = √100 = 10 m
Area of tarpaulin to make the tent = πrl
= 3.14 × 6 × 10 = 188.40m2
Let, the length of 3 m wide tarpaulin = L, therefore, the area of tarpaulin required = 3 × L
According to question,
3 × L = 188.40 ⇒ L = 188.40/3 = 62.80 m
Extra tarpaulin for stitching margins and wastage = 20 cm = 0.20 m
Therefore, the total length of tarpaulin = 62.80 + 0.20 = 63 m
Hence, the length of 3 m wide tarpaulin is 63 m to make the tent.
Q6. The slant height and base diameter of conical tomb are 25m and 14 m respectively. Find the cost of white-washing its curved surface at the rate of Rs. 210 per 100 m2. (Assume π = 22 / 7).
Ans: Radius of conical tomb r = 14/2 = 7 m and slant height / = 25 m/
Curved surface area of conical tomb = πrl
= 22/7 × 7 × 25 = 550 m2
Cost of white washing at the rate of ₹ 210 per 100 m2 = ₹550 × 210/100 = ₹1155
Hence, the cost of white washing curved surface area is ₹ 1155.
Q.7. A joker’s cap is in the form of right circular cone of base radius 7 cm and height 24cm. Find the area of the sheet required to make 10 such caps. (Assume π = 22 / 7)
Ans: Radius of conical cap, r = 7 cm
Height of conical cap, h = 24cm 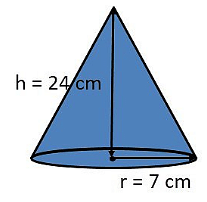 We know that, l2 = (r2 + h2)
We know that, l2 = (r2 + h2)
⇒ l2 = 72 + 242 = 49 + 576 = 625 ⇒ l = √625 = 25 cm
Area of sheet required to make 1 cap = πrl
= 22/7 × 7 × 25 = 550 cm2
Therefore, area of sheet required to make 10 such caps = 10 × 550 = 5500 cm2
Hence, area of sheet to make 10 such caps is 5500 cm2.
Q8. A bus stop is barricaded from the remaining part of the road, by using 50 hollow cones made of recycled cardboard. Each cone has a base diameter of 40 cm and height 1 m. If the outer side of each of the cones is to be painted and the cost of painting is Rs. 12 per m2, what will be the cost of painting all these cones? (Use π = 3.14 and take √(1.04) = 1.02).
Ans: Radius of cone r = 40/2 = 20 cm = 0.2 m and height h = 1 m
Let the slant height = l m
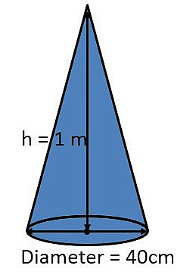 We know that l2 = r2 + h2
We know that l2 = r2 + h2
⇒ l2= (0.2)2 + 12 = 0.04 + 1 = 1.04
⇒ l= √1.04 = 1.02 m
Curved surface area of cone = πrl
= 3.14 × 0.2 × 1.02 = 6.4056m2
Curved surface area of 50 cones
= 50 × 6.4056
= 32.028 m2
Cost of painting at the rate of ₹12 per m2
= ₹12 × 32.028
= ₹384.34 (approx.)
Hence, the cost of painting the curved surface of 50 cones is ₹384.34
Exercise 11.2
Q1. Find the surface area of a sphere of radius:
(i) 10.5cm
(ii) 5.6cm
(iii) 14cm
(Assume π = 22 / 7)
Ans: (i) Radius of sphere r = 10.5 cm
Surface area of sphere = 4πr2
= 4 × 22/7 × 10.5 × 10.5 = 4 × 22 × 1.5 × 10.5 = 1386.00 cm2
Hence, the surface area of sphere is 1386 cm2.
(ii) Radius of sphere r = 5.6 cm
Surface area of sphere = 4πr2
= 4 × 22/7 × 5.6 × 5.6 = 4 × 22 × 0.8 × 5.6 = 394.24 cm2
Hence, the surface area of sphere is 394.24 cm2.
(iii) Radius of sphere r = 14 cm
Surface area of sphere = 4πr2
= 4 × 22/7 × 14 × 14 = 4 × 22 × 2 × 14 = 2464 cm2
Hence, the surface area of sphere is 2464 cm2.
Q2. Find the surface area of a sphere of diameter:
(i) 14 cm
(ii) 21 cm
(iii) 3.5 cm
(Assume π = 22 / 7)
Ans: (i) Radius of sphere r = 14/2 = 7 cm
Surface area of sphere = 4πr2
= 4 × 22/7 × 7 × 7 = 4 × 22 × 7 = 616 cm2
Hence, the surface area of sphere is 616 cm2.
(ii) Radius of sphere r = 21/2 = 10.5 cm
Surface area of sphere = 4πr2
= 4 × 22/7 × 10.5 × 10.5 = 4 × 22 × 4.5 × 10.5 = 1386 cm2
Hence, the surface area of sphere is 1386 cm2.
(iii) Radius of sphere r = 3.5/2 = 1.75 cm
Surface area of sphere = 4π2
= 4 × 22/7 × 1.75 × 1.75 = 4 × 22 × 0.25 × 1.75
= 38.50 cm2
Hence, the surface area of sphere is 38.5 cm2.
Q3. Find the total surface area of a hemisphere of radius 10 cm. [Use π = 3.14]
Ans: Radius of hemisphere r = 10 cm
Surface area of hemisphere = 3πr2
= 3 × 3.14 × 10 × 10 = 942 cm2
Hence, the total surface area of hemisphere is 942 cm2.
Q4. The radius of a spherical balloon increases from 7 cm to 14 cm as air is being pumped into it. Find the ratio of surface areas of the balloon in the two cases.
Ans: Let r be the initial radius and R be the increased radius of balloons.
r = 7cm and R = 14cm
Ratio of the surface area =4πr2/4πR2
= r2/R2
= (7 × 7)/(14 × 14) = 1/4
Thus, the ratio of surface areas = 1 : 4
Q5. A hemispherical bowl made of brass has inner diameter 10.5 cm. Find the cost of tin-plating it on the inside at the rate of Rs 16 per 100 cm2. (Assume π = 22 / 7)
Ans: Radius of the bowl (r) = 10.5/2 cm = 5.25 cm
Curved surface area of the hemispherical bowl = 2πr2
= (2 × 22/7 × 5.25 × 5.25) cm2
= 173.25 cm2
Rate of tin - plating is = ₹16 per 100 cm2
Therefor, cost of 1 cm2 = ₹16/100
Total cost of tin-plating the hemisphere bowl = 173.25 × 16/100
= ₹27.72
Q6. Find the radius of a sphere whose surface area is 154 cm2. (Assume π = 22/7)
Ans: Let r be the radius of the sphere.
Surface area = 154 cm2
⇒ 4πr2 = 154
⇒ 4 × 22/7 × r2 = 154
⇒ r2 = 154/(4 × 22/7)
⇒ r2 = 49/4
⇒ r = 7/2 = 3.5 cm
Q7. The diameter of the moon is approximately one fourth of the diameter of the earth. Find the ratio of their surface areas.
Ans: Let the diameter of earth be r and that of the moon will be r/4
Radius of the earth = r/2
Radius of the moon = r/8
Ratio of their surface area = 4π(r/8)2/4π(r/2)2
= (1/64)/(1/4)
= 4/64 = 1/16
Thus, the ratio of their surface areas is 1:16
Q8. A hemispherical bowl is made of steel, 0.25 cm thick. The inner radius of the bowl is 5cm. Find the outer curved surface of the bowl. (Assume π = 22 / 7)
Ans:  Internal radius of hemispherical bowl r = 5 cm and thickness = 0.25 cm
Internal radius of hemispherical bowl r = 5 cm and thickness = 0.25 cm
Therefore,
The outer radius of hemispherical bowl
= R = 5 + 0.25 = 5.25 cm
Outer curved surface area of hemispherical bowl = 2πR2
= 2 × 22/7 × 5.25 × 5.25
= 2 × 22 × 0.75 × 5.25
= 173.25 cm2
Hence, the outer curved surface area of hemispherical bowl is 173.25 cm2.
Q9. A right circular cylinder just encloses a sphere of radius r (see Fig). Find
(i) surface area of the sphere,
(ii) curved surface area of the cylinder,
(iii) ratio of the areas obtained in(i) and (ii).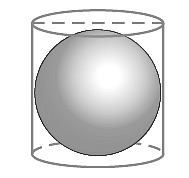 Ans: (i) Radius of sphere = radius of cylinder = r
Ans: (i) Radius of sphere = radius of cylinder = r
Hence, the surface area of sphere = 4πr2
(ii) Radius of cylinder = r and height h = diameter of sphere = 2r
Hence, the curved surface area of cylinder = 2πrh = 2πr(2r) = 4πr2
(iii) Now, Surface area of sphere/Curved surface area of cylinder = 4πr2/4πr2 = 1/1
Hence, the ratio of surface area of sphere to curved surface area of cylinder is 1 : 1.
Exercise 11.3
Q1. Find the volume of the right circular cone with
(i) radius 6 cm, height 7 cm
(ii) radius 3.5 cm, height 12 cm (Assume π = 22 / 7)
Ans: (i) Radius (r) = 6 cm
Height (h) = 7 cm
Volume of the cone = 1/3 πr2h
= (1/3 × 22/7 × 6 × 6 × 7) cm3
= 264 cm3
(ii) Radius (r) = 3.5 cm
Height (h) = 12 cm
Volume of the cone = 1/3 πr2h
Volume of the cone = 1/3 πr2h
= 154 cm3
Q2. Find the capacity in litres of a conical vessel with
(i) radius 7 cm, slant height 25 cm
(ii) height 12 cm, slant height 13 cm (Assume π = 22 / 7)
Ans: (i) Radius (r) = 7 cm
Slant height (l) = 25 cm
Let h be the height of the conical vessel.
∴ h = √l2 - r2
⇒ h = √252 - 72
⇒ h = √576
⇒ h = 24 cm
Volume of the cone = 1/3 πr2h
= (1/3 × 22/7 × 7 × 7 × 24) cm3
= 1232 cm3
Capacity of the vessel = (1232/1000) = 1.232 litres
(ii) Height (h) = 12 cm
Slant height (l) = 13 cm
Let r be the radius of the conical vessel.
∴ r = √l2 - h2
⇒ r = √132 - 122
⇒ r = √25
⇒ r = 5 cm
Volume of the cone = 1/3 πr2h
= (1/3 × 22/7 × 5 × 5 × 12) cm3
= (2200/7) cm3
Capacity of the vessel = (2200/7000) l = 11/35 litres
Q3. The height of a cone is 15cm. If its volume is 1570cm3, find the diameter of its base. (Use π = 3.14)
Ans: Height (h) = 15 cm
Volume = 1570 cm3
Let the radius of the base of cone be r cm
∴ Volume = 1570 cm3
⇒ 1/3 πr2h = 1570
⇒ 13 × 3.14 × r2 × 15 = 1570
⇒ r2 = 1570/(3.14×5) = 100
⇒ r = 10 cm
Diameter of base = 2r = 2 x 10 = 20 cm
Q4. If the volume of a right circular cone of height 9 cm is 48π cm3, find the diameter of its base.
Ans: Given height of a cone, h = 9 cm
Volume of the cone = 48
(1/3)r2h = 48
(1/3)r2 × 9 = 48
3r2 = 48
r2 = 48/3 = 16
r = 4
So diameter = 2 × radius
= 2 × 4
= 8 cm
Hence the diameter of the cone is 8 cm.
Q5. A conical pit of top diameter 3.5 m is 12 m deep. What is its capacity in kilolitres? (Assume π = 22 / 7)
Ans: Radius of pit r = 3.5/2 = 1.75 m and height h = 12 m.
Volume of pit = 1/3 πr2h
= 1/3 × 22/7 × 1.75 × 1.75 × 12 = 38.5 m3
= 38.5 Kilolitres [∴ 1 m3 = 1 kilolitres]
Hence, the capacity of the pit is 38.5 kilolitres.
Q6. The volume of a right circular cone is 9856 cm3. If the diameter of the base is 28 cm, find
(i) height of the cone
(ii) slant height of the cone
(iii) curved surface area of the cone (Assume π = 22 / 7)
Ans: (i) Diameter of the base of the cone = 28 cm
Radius (r) = 28/2 cm = 14 cm
Let the height of the cone be h cm
Volume of the cone = 13πr2h = 9856 cm3
⇒ 1/3 πr2h = 9856
⇒ 1/3 × 22/7 × 14 × 14 × h = 9856
⇒ h = (9856 × 3)/(22/7 × 14 × 14)
⇒ h = 48 cm
(ii) Radius (r) = 14 m
Height (h) = 48 cm
Let l be the slant height of the cone
l2 = h2 + r2
⇒ l2 = 482 + 142
⇒ l2 = 2304+196
⇒ l2 = 2500
⇒ ℓ = √2500 = 50 cm
(iii) Radius (r) = 14 m
Slant height (l) = 50 cm
Curved surface area = πrl
= (22/7 × 14 × 50) cm2
= 2200 cm2
Q7. A right triangle ABC with sides 5 cm, 12 cm and 13 cm is revolved about the side 12 cm. Find the volume of the solid so obtained.
Ans: If the triangle is revolved about 12 cm side, a cone will be formed.
Therefore, the radius of cone r = 5 cm, height h = 12 cm and slant height l =13 cm.
Volume of solid (cone) = 1/3 πr2h
= 1/3 × π × 5 × 5 × 12 = 100 π cm3
Hence, the volume of solid is 100π cm3.
Q8. If the triangle ABC in the Question 7 is revolved about the side 5cm, then find the volume of the solids so obtained. Find also the ratio of the volumes of the two solids obtained in Questions 7 and 8.
Ans:
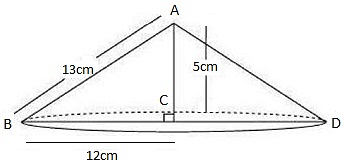 A right-angled ΔABC is revolved about its side 5cm, a cone will be formed of radius as 12 cm, height as 5 cm, and slant height as 13 cm.
A right-angled ΔABC is revolved about its side 5cm, a cone will be formed of radius as 12 cm, height as 5 cm, and slant height as 13 cm.
Volume of cone = (1/3) πr2h; where r is the radius and h be the height of cone
= (1/3) × π × 12 × 12 × 5
= 240 π
The volume of the cones of formed is 240π cm3.
So, required ratio = (result of question 7) / (result of question 8) = (100π) / (240π) = 5 / 12 = 5 : 12.
Q9. A heap of wheat is in the form of a cone whose diameter is 10.5 m and height is 3 m. Find its volume. The heap is to be covered by canvas to protect it from rain. Find the area of the canvas. (Assume π = 22 / 7)
Ans: Radius (r) of heap = (10.5 / 2) m = 5.25
Height (h) of heap = 3m
Volume of heap = (1 / 3)πr2h
= (1 / 3) × (22 / 7) × 5.25 × 5.25 × 3
= 86.625 m3
The volume of the heap of wheat is 86.625 m3. Again,
Area of canvas required = CSA of cone = πrl, where l = 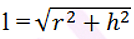
After substituting the values, we have
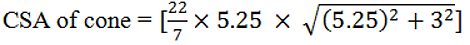
= (22 / 7) × 5.25 × 6.05
= 99.825
Therefore, the area of the canvas is 99.825 m2.
Exercise 11.4
Q1. Find the volume of a sphere whose radius is
(i) 7 cm
(ii) 0.63 m (Assume π = 22 / 7)
Ans: (i) Radius of sphere, r = 7 cm
Using, Volume of sphere = (4 / 3) πr3
= (4 / 3) × (22 / 7) × 73 = 4312 / 3
Hence, volume of the sphere is  (ii) Radius of sphere, r = 0.63 m
(ii) Radius of sphere, r = 0.63 m
Using, volume of sphere = (4 / 3) πr3
= (4 / 3) × (22 / 7) × 0.633 = 1.0478
Hence, volume of the sphere is 1.05 m3 (approx).
Q2. Find the amount of water displaced by a solid spherical ball of diameter
(i) 28 cm
(ii) 0.21 m (Assume π = 22 / 7)
Ans: (i) Radius of spherical ball r = 28/2 = 14 cm
Volume of water displaced by spherical ball = 4/3 πr3
= 4/3 × 22/7 × 14 × 14 × 14
= 4/3 × 22 × 2 × 14 × 14 = 
or =11498.67 cm3
(ii) Radius of spherical ball r = 0.21/2 = 0.105 m
Volume of water displaced by spherical ball = 4/3 πr3
= 4/3 × 22/7 × 0.105 × 0.105 × 0.105 = 4 × 22 × 0.005 × 0.63 × 0.63 = 0.004861 m3
Hence, the volume of water displaced by spherical ball is 0.004861 m3.
Q3. The diameter of a metallic ball is 4.2cm. What is the mass of the ball, if the density of the metal is 8.9 g per cm3? (Assume π = 22 / 7)
Ans: Radius of metallic ball r = 4.2/2 = 2.1 cm
Therefore, the volume of metallic ball = 4/3 πr3
= 4/3 × 22/7 × 2.1 × 2.1 × 2.1
= 4 × 22 × 0.1 × 2.1 × 2.1 = 38.808 cm3
Here, the mass of 1 cm3 = 8.9 g
So, the mass of 38.808 cm3 = 8.9 × 38.808 = 345.39 g (approx.)
Hence, the mass of the ball is 345.39 gram.
Q4. The diameter of the moon is approximately one-fourth of the diameter of the earth. What fraction of the volume of the earth is the volume of the moon?
Ans: Let the diameter of earth be “d”. Therefore, the radius of earth will be will be d/2
Diameter of moon will be d / 4 and the radius of moon will be d/8
Find the volume of the moon:
Volume of the moon = (4 / 3) πr3 = (4 / 3) π (d / 8)3 = 4 / 3π(d3 / 512)
Find the volume of the earth:
Volume of the earth = (4 / 3) πr3 = (4 / 3) π (d / 2)3 = 4 / 3π(d3 / 8)
Fraction of the volume of the earth is the volume of the moon
Volume of moon is of the 1 / 64 volume of earth.
Q5. How many litres of milk can a hemispherical bowl of diameter 10.5cm hold? (Assume π = 22 / 7)
Ans: Diameter of hemispherical bowl = 10.5 cm
Radius of hemispherical bowl, r = 10.5 / 2 cm = 5.25 cm
Formula for volume of the hemispherical bowl = (2 / 3) πr3
Volume of the hemispherical bowl = (2 / 3) × (22 / 7) × 5.253 = 303.1875
Volume of the hemispherical bowl is 303.1875 cm3
Capacity of the bowl = (303.1875) / 1000 L = 0.303 litres(approx.)
Therefore, hemispherical bowl can hold 0.303 litres of milk.
Q6. A hemi spherical tank is made up of an iron sheet 1cm thick. If the inner radius is 1 m, then find the volume of the iron used to make the tank. (Assume π = 22/7)
Ans: Inner Radius of the tank, (r) = 1m
Outer Radius (R) = 1.01m
Volume of the iron used in the tank = (2 / 3) π (R3 – r3)
Put values,
Volume of the iron used in the hemispherical tank = (2 / 3) × (22 / 7) × (1.013 – 13) = 0.06348
So, volume of the iron used in the hemispherical tank is 0.06348 m3.
Q7. Find the volume of a sphere whose surface area is 154 cm2. (Assume π = 22 / 7)
Ans: Surface area of sphere A = 154 cm2
Let, the radius of sphere = r cm
We know that the surface area of sphere = 4πr2 
Volume of surface 4/3 πr3

Hence, the volume of sphere is  .
.
Q8. A dome of a building is in the form of a hemisphere. From inside, it was white-washed at the cost of ₹ 4989.60. If the cost of white-washing is ₹ 20 per square meter, find the
(i) Inside surface area of the dome
(ii) volume of the air inside the dome (Assume π = 22 / 7)
Ans: (i) Let the internal radius of dome = r m
Internal surface area of dome = 2πr2
Cost of white washing at the rate of ₹2 = 2πr2 × ₹2 = ₹4πr2
⇒ ₹4πr2 = ₹498.96
⇒ 4 × 22/7 × r2 = 498.96
Therefore, the internal surface of dome = 2πr2
= 2 × 22/7 × (6.3)2
= 2 × 22/7 × 6.3 × 6.3
= 2 × 22 × 0.9 × 6.3
= 249.48 m2
Hence, the inside surface area of the dome is 249.48 m2.
(ii) Volume of the air inside the dome = 2/3 πr3
= 2/3 × 22/7 × (6.3)3
= 2/3 × 22/7 × 6.3 × 6.3 × 6.3
= 2 × 22 × 0.3 × 6.3 × 6.3
= 523.9 cm3
= Hence, the volume of the air inside the dome is 523.9 cm3.
Q9. Twenty-seven solid iron spheres, each of radius r and surface area S are melted to form a sphere with surface area S’. Find the
(i) radius r’ of the new sphere,
(ii) ratio of Sand S’.
Ans: Volume of the solid sphere = (4 / 3)πr3
Volume of twenty seven solid sphere = 27 × (4 / 3)πr3 = 36 πr3
(i) New solid iron sphere radius = r’
Volume of this new sphere = (4/3)π(r’)3
(4 / 3)π(r’)3 = 36 πr3
(r’)3 = 27r3
r’= 3r
Radius of new sphere will be 3r (thrice the radius of original sphere)
(ii) Surface area of iron sphere of radius r, S = 4πr2
Surface area of iron sphere of radius r’= 4π (r’)2
Now
S / S’ = (4πr2) / ( 4π (r’)2)
S / S’ = r2 / (3r’)2 = 1 / 9
The ratio of S and S’ is 1: 9.
Q10. A capsule of medicine is in the shape of a sphere of diameter 3.5 mm. How much medicine (in mm3) is needed to fill this capsule? (Assume π = 22 / 7)
Ans: Radius of capsule r = 3.5/2 = 1.75 mm
Volume of medicine to fill the capsule = 4/3πr3
= 4/3 × 22/7 × 1.75 × 1.75 × 1.75
= 4/3 × 22 × 0.25 × 1.75 × 1.75
= 22.46 mm3 (approx.)
Hence, 22.46 mm3 medicine is required to fill this capsule.
|
44 videos|412 docs|54 tests
|
FAQs on NCERT Solutions for Class 9 Maths Chapter 11 - Surface Areas and Volumes
| 1. What are the formulas for calculating surface areas and volumes of different shapes? |  |
| 2. How do you derive the volume of a cylinder? |  |
| 3. What is the difference between surface area and volume? |  |
| 4. Why are surface areas and volumes important in real-life applications? |  |
| 5. Can you explain how to solve a problem involving the surface area of a composite shape? |  |






















