Class 10 Maths Chapter 3 Question Answers - Pair of Linear Equations in Two Variables
Q1. Find the value of k so that graphs of
2x - ky = 9
6x - 9y = 18 will be parallel.
Sol.For the graph of equations of a system of linear equations to be parallel.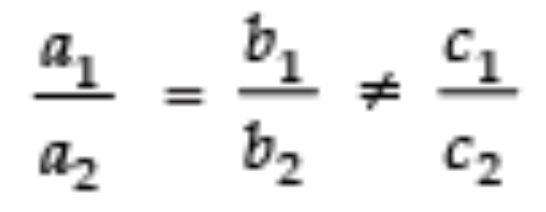
∴ 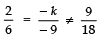
⇒ 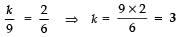
Q2. Find the value of k so that the point (3, k) lies on the line represented by x - 5y = 5.
Sol. Substituting (3, k) in x - 5y = 5, we have:
3 - 5k = 5
⇒ - 5k = 5 - 3 = 2
⇒
Q3. Determine the value of k for which
kx + 3y = k - 3
12x + ky = k represent coincident lines.
Sol. ∵ For coincident lines,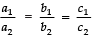
∴ 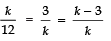
⇒ 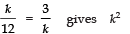
= 36 ⇒ k = 6
Also 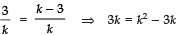
⇒ 6k = k2 ⇒ k = 6
Q4. If the system of linear equations,
3x + 2y - 4 = 0
px - y - 3 = 0 represents intersecting lines, then find p.
Sol. a1 = 3, b1 = 2, c1 = - 4
a2 = p, b2 = - 1, c2 = - 3
For intersecting lines [i.e., having a unique solution]: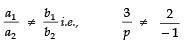
⇒ 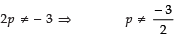
Q5. If (a + b) x + (2a - b) y = 21 and 2x + 3y = 7 has infinitely many solutions, then what is ‘a’ and ‘b’?
Sol. Here A1 = (a + b), B1 = (2a - b),
C1 = - 21
A2 = 2, B2 = 3, C2 = - 7
For infinite number of roots,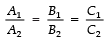
⇒ 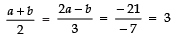
∴ 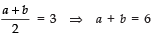
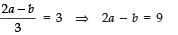
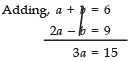
⇒ a = 15/3 = 5
a + b =6 ⇒ b = 6 − 5 = 1
Thus, a = 5 and b = - 1
Q6. Write the relation between the coefficients for which the pair ax + by = c, lx + my = x has a unique solution.
Sol. A1 = a, B1 = b, C1 = c
A2 = l, B2 = m, C2 = n
For a unique solution,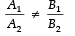
i.e., 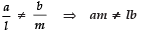
Q7. Check if the pair of linear equations 3x + 6 = 10y and 2x - 15y + 3 = 0 is consistent or not?
Sol. Here, a1 = 3, b1 = - 10, c1 = 6
a2 = 2, b2 = - 15, c2 = 3
For the given pair of linear equations to be consistent,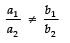
⇒ 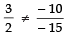
⇒  which is true.
which is true.
∴The given system of linear equations is consistent.
Q8. For what value of k,
2x + 2y + 2 = 0
4x + ky + 8 = 0 will have unique solution.
Sol. Here, a1 = 2, b1 = 2, c1 = 2
a2 = 4, b2 = k, c2 = 8
For the given system of linear equations to have a unique solution.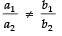
∴ 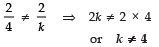
Q9. Find the value of k for which the following system represents parallel lines:
=
2 (k - 1) x + y = 1
Sol. We have
=
and 2 (k - 1) x + y = 1
for parallel lines,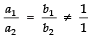
⇒ 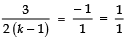
⇒ 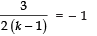
⇒ 3= − 2 (k − 1)
⇒ 3= − 2k + 2
⇒ 3 − 2= − 2k
⇒ 1= − 2k
⇒ 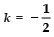
Q10. What is the point of intersection of the line 3x + 7y = 14 and the y-axis
Sol. ∵ For the point of intersection of a line and the y-axis, we put x = 0.
∴ 3x + 7y = 14
⇒ 3 (0) + 7y = 14
⇒ 7y = 14 ⇒ y = 2
∴ The point is (0, 2).
Q11. For what value of ‘a’ does the following pair of linear equations have infinitely many solutions?
4x - 3y - (a - 2) = 0, 8x - 6y - a = 0
Sol. We have:
4x - 3y - (a - 2) = 0
8x - 6y - a = 0
For infinitely many solutions, we have: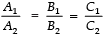
⇒ 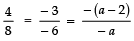
⇒ 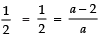
⇒ 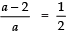
⇒ 2a − 4= a
⇒ a = 4
Q12. Find the number of solutions of the following pair of linear equations:
x + 2y - 8 = 0
2x + 4y = 16
Sol.We have:
x + 2y - 8 = 0
2x + 4y - 16 = 0
Here,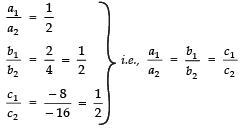
∴ The given system of equations has an infinite number of solutions.
Q13. Find the value (s) of ‘k’ for which the system of linear equations has no solutions.
kx + 3y = k - 2
12x + ky = k
Sol.The given pair of linear equations are:
kx + 3y = k - 2 ...(1)
12x + ky = k ...(2)
For no solution of (1) and (2), we must have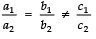
i.e., 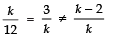
⇒ 
i.e., k2 = 36 and 3k ≠ k2 − 2k
i.e., k = ± 6 and 3 ≠ k − 2
or k = ± 6 and k ≠ 5 ⇒ k = ± 6
Q14. Write whether the following pair of linear equations is consistent or not:
x + y = 14
x - y = 4
Sol. Here,
Since, for a consistent pair of linear equations, , which is true for the given system [∵ 1 ≠ (- 1)]
Thus, it is a consistent pair of linear equations.
Q15. Find the value of k so that the following system of equations has no solution:
3x - y - 5 = 0
6x - 2y - k = 0
Sol. We have:
Here, 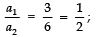
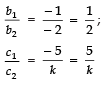
For no solution,
or 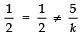
⇒ 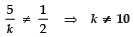
Q16. For what value of ‘a’, the point (3, a) lies on the line represented by 2x - 3y = 5?
Sol. Since, (3, a) lies on the equation
2x - 3y = 5
∴ (3, a) must satisfy this equation.
⇒ 2 (3) - 3 (a) = 5
⇒6 - 3a = 5
⇒ - 3a = 5 - 6 = - 1
⇒
Thus the required value of a is 1/3.
|
127 videos|584 docs|79 tests
|
FAQs on Class 10 Maths Chapter 3 Question Answers - Pair of Linear Equations in Two Variables
| 1. What is a pair of linear equations in two variables? |  |
| 2. How can we solve a pair of linear equations in two variables? |  |
| 3. What is the importance of solving a pair of linear equations in two variables? |  |
| 4. Can a pair of linear equations in two variables have more than one solution? |  |
| 5. How can we determine the consistency of a pair of linear equations in two variables? |  |

















