Class 10 Maths Chapter 11 Question Answers - Surface Areas and Volumes
Q1. Rohan is in the business of supplying water. He has three types of tankers of inner diameter 1.0 m to supply water to the customers. The length of the tankers is 6 m. [use π = 3.14] He decided to serve his customers with type ‘A’ tankers.
(a) Find the volume of a tanker of type A.
(b) Which tanker has the minimum capacity?
(c) Which mathematical concept is used in the above problem?
(d) By choosing a tanker of ‘type-A’, which value is depicted by Rohan?
Sol. ∵ Diameter = 1.0 m
∴ Radius = 1/2 m
Length of the tank = 6 m ⇒ h = 6 m
(a) Volume of the tanker of type-A = πr2h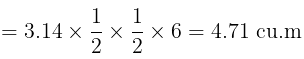
(b) Volume of the tanker of ‘type-B’ = [Volume of the tanker-A] – [Volume of hemisphere]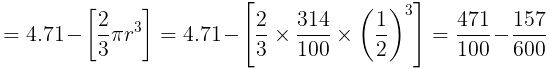
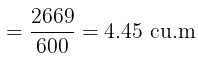
Volume of the tanker of ‘type-C’ = [Volume of the tanker-A] – [Volume of the cone]
= [4.71 – 0.157] cu. m = [0.157] cu. m
= 4.553 cu. m
Thus, the tanker of ‘type-B’ has a minimum capacity of 4.45 cu. m.
(c) Mensuration [volume of solid figures]
(d) Honesty
Q2. Shankar, a ‘Kulfi-vendor’ has three types (spherical, conical and cuboidal) of containers for making Kulfi :
He decided to serve the customers with a ‘Type I’ container.
(a) Find the volume of the container ‘type-I’.
(b) Which container has the minimum capacity?
(c) Which mathematical concept is used in this problem?
(d) By choosing to prepare to sell Kulfi using a container of ‘Type-I’, which value is depicted by Shankar?
Sol. (a) Finding the volume of Type-I container:
∵ Diameter = 7 cm
⇒ The volume of the container of ‘type-I’
= 4/3 πr3
(b) Volume of conical (type-II) container
Volume of cuboidal (type-III) container
Obviously, the capacity of the cuboidal (type-III) container is minimum, which is 122.5 cu. cm.
(c) Volume of solid bodies (mensuration)
(d) Honesty
Q3. Prashant has undertaken a contract to build a wall of 9m long, 2.5m thick and 6m high. His labour is to be calculated according to the number of bricks used to complete the wall. In the market three types of bricks are available.
Type-I:Each measuring 25cm × 11.25cm × 6cm
Type-II: Each measuring 20cm × 8cm × 10cm
Type-III: Each measuring 25cm × 10cm × 9cm
Prashant used bricks of type-III.
(a) Find the number of bricks of type-III required to build the wall.
(b) In which case, the maximum number of bricks will be used?
(c) Which mathematical concept is used in the above problem?
(d) By using the bricks of type-III, which value is depicted by Prashant?
Sol. Volume of a brick of type-I =l × b × h
= 25 cm × 11.25 cm × 6 cm = 1687.50 cm3
Volume of a brick of type-II
= l × b × h = 20 cm × 8 cm × 10 cm
= 1600 cm3
Volume of a brick of type-III
= l × b × h = 25 cm × 10 cm × 9 cm
= 2250 cm3
Volume of the wall
= l × b × h = 9 × 2.5 × 6 m3
= 135 × 106 cm3
(a) ∴ Number of bricks of type-III required for building the wall
(b) Number of bricks required for building the wall using type-I bricks:
Number of bricks of type-II required for building the wall
⇒ In case of type-II, the maximum number of bricks will be required.
(c) Volume of solid bodies (mensuration)
(d) Honesty
Q4. Sampat has set up his juice shop. He has three types of cylindrical glasses as given below :
A cylindrical glass with inner diameter 7 cm and height as 10 cm.
A cylindrical glass with inner diameter 4 cm and height as 14 cm.
A cylindrical glass with inner diameter 14 cm and height as 4 cm.
He decided to serve the customers in ‘Type-I’ of glasses.
(a) Find the volume of the glass of type-I.
(b) Which glass has the minimum capacity?
(c) Which mathematical concept is used in the above problem?
(d) By choosing a glass of type-I, which value is depicted by juice seller Sampat?
Sol. (a) Diameter of glass of type-I = 7 cm
∴ Radius = 7/2 cm
Height = 10 cm
⇒ Volume = πr2h
(b) Diameter of glass of type-II
= 4cm
∴ Radius = 2cm
Height = 14 cm
⇒ Volume = πr2h
= 176 cm3
Diameter of glass of type-III
= 14 cm
∴ Radius = 14/2 cm = 7 cm
Height = 4 cm
⇒ Volume = πr2h
= 22×28 cm3
= 308 cm3
⇒ The glass of type-II has the minimum capacity.
(c) Mensuration [volume of solid bodies]
(d) Honesty.
Q5. A community well with 10 m inside diameter is dug 14 m deep. For spreading the earth taken out of it, there are two options :
(i) It is spread all around the well to a width of 6 m to form an embankment.
(ii) It is spread evenly on a rectangular surface of 25m × 11m.
The contractor charges according to the height of the spread over mud. He charges by choosing the option-(i).
(a) Find the height of the spread over mud in both options.
(b) Which mathematical concept is involved in the above problem?
(c) In which case cost of digging the well is less?
(d) Which values are depicted by the contractor by charging according to option-(i)?
Sol. Inside diameter of the well = 10 m
⇒ Inside radius of the well = 5 m
Depth of the well = 14 m
∵ Volume of the earth dugout = πr2h
= 22 × 5 × 5 × 2 m3
= 1100 m3
(a) Height of the spreadover mud: option-(i)
Area of the shaded region (base of the spread over mud)
= πR2 – πr2
= π [R2 – r2]
[Here: R = 11 m and r = 5 m]
= π [(R – r) (R + r)]
Let the height of the spread over mud (embankment) be h1,
option-(ii)
Let the height of the spread over mud = h2,
(b) Mensuration [volume of solid bodies]
(c) ∵ The height of spread over mud is less in option-(i).
∴ The cost of digging the well is less in option-(i).
(d) Community service and honesty.
Q6. A contractor is entrusted to erect a tent for flood victims. He is allowed a fixed amount for this task. He has two options :
(i) to erect a tent that is cylindrical up to a height of 3 m and conical above it. The diameter of the base is 105 m and the slant height of the conical part is 53 m.
(ii) to erect the tent as described in option(i), only replacing the conical part as a hemispherical part.
The contractor chooses option-(ii) and decides to donate the extra (difference) canvas to be used in this case.
(a) How much canvas is donated by the contractor?
(b) Which mathematical concept is used in the above problem?
(c) By choosing the option-(ii) to erect the tent, which value is depicted by the contractor?
Sol. (a)
Total canvas used in option-(i) = [Curved surface area + [Curved surface area of the cylindrical part] of the conical part] = [2πrh + πrl]
Total canvas used in option-(ii) = [Curved surface area + [Curved surface area of cylindrical part] of hemispherical part]=[2πrh + 2πr2]
Difference in areas of canvas required in the above two options.
= 18315 – 9733 m2
= 8582 m2
⇒ The contractor donated 8582 m2 of canvas.
(b) Mensuration [volume of solid bodies]
(c) Patriotism
Q7. Sushant has a vessel, of the form of an inverted cone, open at the top, of height 11 cm and radius of top as 2.5 cm and is full of water. Metallic spherical balls each of diameter 0.5 cm are put in the vessel due to which 2/5th of the water in the vessel flows out. Find how many balls were put in the vessel. Sushant made the arrangement so that the water that flows out irrigates the flower beds. What value has been shown by Sushant?
Sol. Base radius of the cone (r) = 2.5cm
Height of the concial part (h) = 11cm
Using V = 1/3 πr2h, the volume of the conical vessel.
of water is flown out due to ‘n’ spherical balls each of radius = 0.5 cm
∵ Volume of n balls =
⇒ n[volume of one ball]
⇒
Thus, the required number of lead shots = 55
Value: To keep the plants green for pollution-free surroundings.
|
127 videos|584 docs|79 tests
|
FAQs on Class 10 Maths Chapter 11 Question Answers - Surface Areas and Volumes
| 1. How do you find the surface area of a cube? |  |
| 2. What is the formula for finding the volume of a cylinder? |  |
| 3. How can you find the surface area of a cone? |  |
| 4. What is the formula for finding the volume of a sphere? |  |
| 5. How do you find the surface area of a rectangular prism? |  |

















