NCERT Solutions for Class 10 Maths Chapter 11 - Areas Related to Circles (Excercise 11.1)
Page No 158
Use π = 22/7 (unless stated otherwise)
Q1: Find the area of a sector of a circle with radius 6 cm if angle of the sector is 60°.
Sol: Here,
r = 6 cm
θ = 60°
∴ Using, the Area of a sector =
We have,
Area of the sector with r = 6 cm and θ = 60°
Q2: Find the area of a quadrant of a circle whose circumference is 22 cm.
Sol: Let the radius of the circle = r
∴ 2πr = 22
⇒
Here θ = 90°
∴ Area of the quadrant of the circle,
Q3: The length of the minute hand of a clock is 14 cm. Find the area swept by the minute hand in 5 minutes.
Sol: [Length of minute hand] = [radius of the circle]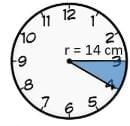 ⇒ r = 14 cm
⇒ r = 14 cm
∵ Angle swept by the minute hand in 60 minutes = 360°
∴ Angle swept by the minute hand in 5 minutes =
Now, area of the sector with r = 14 cm and θ = 30°
Thus, the required area swept by the minute hand by 5 minutes = 154/3 cm2.
Q4: A chord of a circle of radius 10 cm subtends a right angle at the centre. Find the area of the corresponding (i) minor segment (ii) major sector. (Use π = 3.14)
Sol: Given the radius of the circle = 10 cm
Angle subtend by chord at centre = 90° ...(i)
(i) Area of the minor segment = (Area of the sector OAB) - (Area of ΔAOB formed with radius and chord)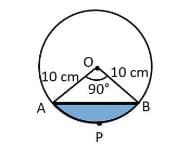
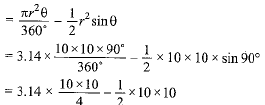
= 3.14 x 25 - 50 = 78.5 - 50 = 28.5 cm2
(ii) Area of major sector = Area of the circle – Area of the minor sector
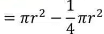
=(1- 1/4) πr²
=3/4 πr²
=3/4 x π(10)2
= (3.14×102)-78.5
= 235.5 cm2
Q5: In a circle of radius 21 cm, an arc subtends an angle of 60° at the centre. Find:
(i) the length of the arc
(ii) area of the sector formed by the arc
(iii) area of the segment formed by the corresponding
Sol:
Here, radius = 21 cm and θ = 60°
(i) Circumference of the circle = 2πr
(ii) Area of the sector with sector angle 60°
(iii) Area of the segment formed by the corresponding chord = area of the sector - area of the Δ formed between chord and radius of the circle
Q6: A chord of a circle of radius 15 cm subtends an angle of 60° at the centre. Find the areas of the corresponding minor and major segments of the circle. (Use π = 3.14 and √3 = 1.73)
Sol:
Radius of the circle = 15 cm
Central angle subtends by chord = 600
Area of sector = 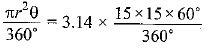
= 117.75 cm2
Area of the triangle formed by radii and chord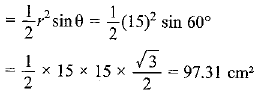
Area of the minor segment = Area of the sector -Area of the triangle formed by radii and chord
= 117.75-97.31 =20.44 cm2
Area of the circle = πr2
= 3.14 x 15 x 15 = 706.5 cm2
Area of the major segment = Area of the circle - Area of the minor segment
= 706.5 - 20.44 = 686.06 cm2
Q7: A chord of a circle of radius 12 cm subtends an angle of 120° at the centre. Find the area of the corresponding segment of the circle. (Use π = 3.14 and √3 = 1.73)
Sol: Here, θ = 120° and r = 12 cm
In Δ OAB, ∠O = 120°
⇒∠A + ∠B = 180° − 120 = 60°
∵ OB = OA = 12 cm ⇒∠A = ∠B = 30°
So,
⇒
In right Δ AMO, 122 − 62 = AM2
⇒ 144 − 36 = AM2
⇒ 108 = AM2
⇒
⇒
⇒
Now, from (2),
= 36 × 1.73 cm2 = 62.28 cm2 ...(3)
From (1) and (3)
Area of the minor segment = [Area of minor segment] − [Area of Δ AOB]
= [150.72 cm2] − [62.28 cm2] = 88.44 cm2.
Q8: A horse is tied to a peg at one corner of a square shaped grass field of side 15 m by means of a 5 m long rope (see figure).
Find:
(i) the area of that part of the field in which the horse can graze.
(ii) the increase in the grazing area if the rope were 10 m long instead of 5 m. (Use π = 3.14)
Sol: Here, Length of the rope = 5 m
∴ Radius of the circular region grazed by the horse = 5 m
(i) Area of the circular portion grazed [∵ θ = 90° for a square field.]
(ii) When length of the rope is increased to 10 m,
∴ r = 10 m
⇒ Area of the circular region where θ = 90°.
∴ Increase in the grazing area = 78.5 − 19.625 m2 = 58.875 m2.
Page No 159
Q9: A brooch is made with silver wire in the form of a circle with diameter 35 mm. The wire is also used in making 5 diameters which divide the circle into 10 equal sectors as shown in Fig.
Find:
(i) the total length of the silver wire required.
(ii) the area of each sector of the brooch.
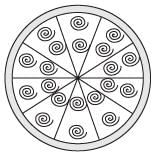
Sol: Diameter of the circle = 35 mm
∴
(i) Diameter (D) = 35 mm
Total number of diameters to be considered= 5
Now, the total length of 5 diameters that would be required = 35×5 = 175
Circumference of the circle = 2πr
Or, C = πD
= 22/7×35 = 110
∴ Total length of the silver wire = 110 + 175 mm = 285 mm
(ii) Since the circle is divided into 10 equal sectors,
∴ Sector angle
⇒ Area of each sector
Q10: An umbrella has 8 ribs which are equally spaced (see figure). Assuming umbrella to be a flat circle of radius 45 cm, find the area between the two consecutive ribs of the umbrella.
Sol: Here, radius (r) = 45 cm
Since circle is divided in 8 equal parts,
∴ Sector angle corresponding to each part
⇒ Area of a sector (part)
∴ The required area between the two ribs
Q 11: A car has two wipers which do not overlap. Each wiper has a blade of length 25 cm sweeping through an angle of 115°. Find the total area cleaned at each sweep of the blades.
Sol: Here, radius (r) = 25 cm
Sector angle (θ) = 115°
∴ Area cleaned by each sweep of the blades [∵ Each sweep will have to and fro movement]
Q12: To warn ships for underwater rocks, a lighthouse spreads a red coloured light over a sector of angle 80° to a distance of 16.5 km.
Find the area of the sea over which the ships are warned. (Use π = 3.14)
Sol: Here, Radius (r) = 16.5 km
Sector angle (θ) = 80°
∴ Area of the sea surface over which the ships are warned
Q13: A round table cover has six equal designs as shown in Fig. If the radius of the cover is 28 cm, find the cost of making the designs at the rate of Rs 0.35 per cm2. (Use √3 = 1.7)
Sol: Here, r = 28 cm
Since, the circle is divided into six equal sectors.
∴ Sector angle
∴ Area of the sector with θ = 60° and r = 28 cm
Now, area of 1 design
= Area of segment APB
= Area of sector − Area of ΔAOB ...(2)
In ΔAOB, ∠AOB = 60°, OA = OB = 28 cm
∴ ∠OAB = 60° and ∠OBA = 60°
⇒ ΔAOB is an equilateral triangle.
⇒ AB = AO = BO
⇒ AB = 28 cm
Draw OM ⊥ AB
∴ In right ΔAOM, we have
⇒
⇒ ...(3)
Now, from (1), (2) and (3), we have:
Area of segment APQ = 410.67 cm2 − 333.2 cm2 = 77.47 cm2
⇒ Area of 1 design = 77.47 cm2
∴ Area of the 6 equal designs = 6 × (77.47) cm2
= 464.82 cm2
Cost of making the design at the rate of Rs 0.35 per cm2,
= Rs 0.35 × 464.82
= Rs 162.68.
Q14: Tick the correct answer in the following: Area of a sector of angle p (in degrees) of a circle with radius R is
Sol: Here, radius (r)= R
Angle of sector (θ)= p°
∴ Area of the sector
Thus, the option is correct.
|
127 videos|584 docs|79 tests
|
FAQs on NCERT Solutions for Class 10 Maths Chapter 11 - Areas Related to Circles (Excercise 11.1)
| 1. What is the formula for the area of a circle? |  |
| 2. How do you find the circumference of a circle? |  |
| 3. What is the relationship between the radius and diameter of a circle? |  |
| 4. How can you find the area of a sector of a circle? |  |
| 5. What is the significance of π (pi) in circle-related calculations? |  |






















